221023_TIL

19,20일에 스터디했던 거 TIL 기록 못 했다.. 기회가 있겠지.
아무튼 오늘 공부한 것만 기록!

공부한 것

1. 선형대수 | 8일간의 선형대수학 2.2절-1: 행렬식의 기하학적 의미: 절댓값편! [행렬, 벡터공간]
   • Keyword & Implication
     • 행렬식의 변환: $R^2 -> R^2$ 를 행렬식으로만 보지 말고, 그림을 그려가며 이해해보자.
     • 행렬식 절댓값의 의미: 행렬식이란 변환한 평행면체의 부피가 0일 때, 행렬 A의 역행렬을 존재하지 않는다.
   • Notation
     • p.5 변환
     • p.9 3차 정사각행렬의 변환식 (?)
       (직접 필기한 이미지는 옮겨두지 않겠음)
   • Key Question
     • 행렬식을 구하는 것이 왜 |ad-bc| 일까? (증명 - 공돌이 수학노트)
       • 기하학적으로 증명 과정을 설명할 수 있는가?
     • det = 0 의 의미에서, 두 벡터가 겹치는 경우 왜 1:1 대응이 안되고, 역함수가 존재하지 않는다고 할 수 있는 걸까?
       • 두 벡터가 겹치는 경우 1:1 대응이 안된다는 의미는?
       • 두 벡터가 동일 선상에 있을 때 ad-bc = 0이 되므로 역함수가 존재할 수 없는 것은 알겠음. 이를 기하학적으로 어떻게 표현할 수 있을까?

2. Statistics | [핵심 확률/통계] 독립 (Independence)
   • Keyword & Implication
     • 독립사건
       • 각 이벤트가 독립일 경우 각사건의 교집합의 확률은 각각의 확률을 곱한 것과 같다.
         (mutually exlusive vs Indepent는 다르다!)
       • E, F, G가 독립일 경우, E는 F와 G로 만든 어떤 이벤트와도 독립이다.
         • $P[E(FUG)] = P(E)P(FUG)$
   • Notation
     • 독립사건 교집합 확률
       • 반대로, 두 사건이 독립적인지 판단하기 위해선 위 식을 만족하는지를 구해보면 알 수 있음.
     • 증명 가능?
       
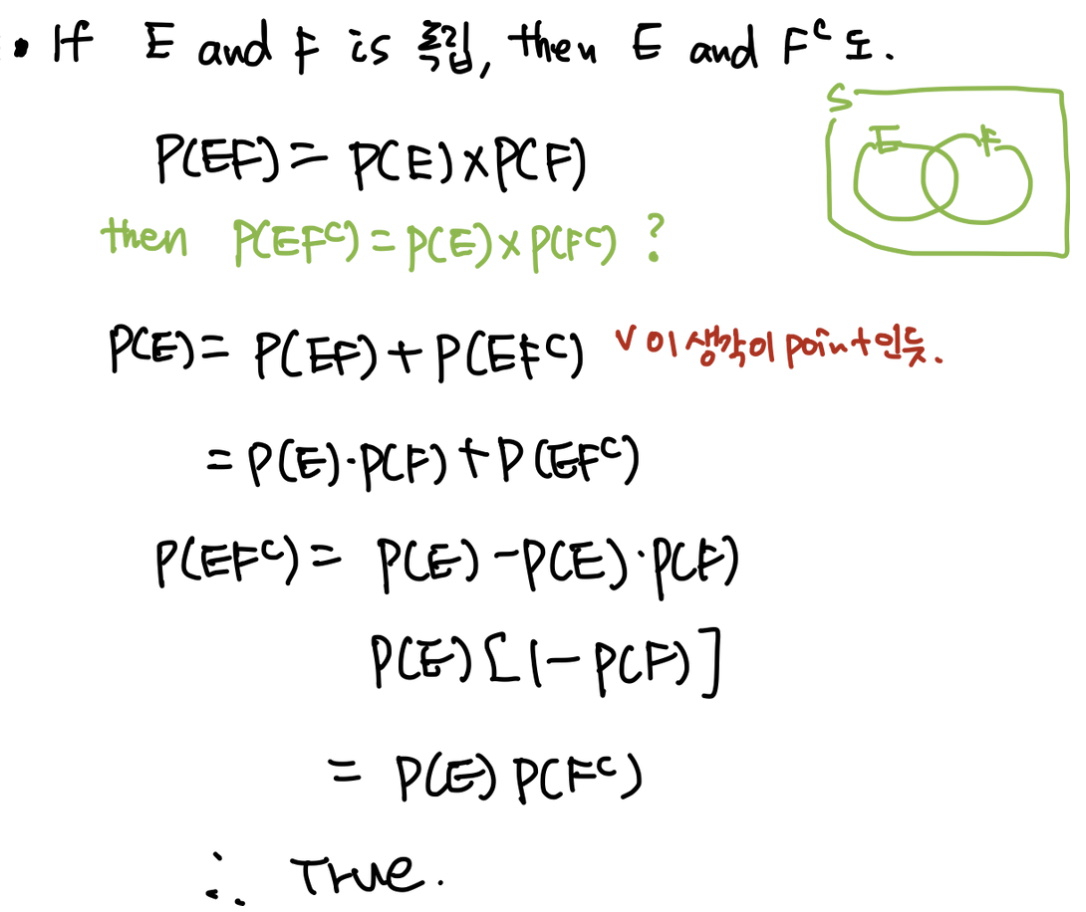
       • 내가 참인지 확인하려는 식에 $P(EF^c)$가 있었으니, 그걸 포함하는 식을 생각해내는게 증명에 있어서 포인트인 것 같다.
   • Key Question
     • 두 사건의 확률이 주어진 경우, 두 사건이 독립적인지 아닌지 구분할 수 있는가?
     • mutually exlusive vs Indepent를 벤다이어그램으로 어떻게 구분해 표현할 수 있을까? (헷갈림)

1. Python | 한 번에 끝내는 딥러닝/인공지능 초격차 패키지Online - lecture5
   • Keyword & Implication
     • list - 생성 / 원소 접근 / 원소 수정 / len()
     • Mean Subtraction / variance / standard deviation / strandardization
   • Notation
     • 수학점수들의 평균 구하기 ⇒ $\mu(mu) = \frac{1}{n} \sum\limits_{i=1}^nx_i$
     • 분산, 표준편차
     • 표준화 (standardization) - 분산 0, 표준편차 1로 변환.
       $x := \frac{x-\mu}{\sigma}$
   • Key Question
     • 분산을 잔차제곱합의 평균 뿐 아니라 위와 같이도 정의할 수 있는 이유? (링크)

2. Time-Series | 딥러닝/머신러닝을 활용한 시계열 데이터분석 - 데이터분석의범위 -기술통계와 추론통계
   • (강의 새로 샀다)
   • Keyword & Implication
     • 기술 통계(Descriptive statistics) / 추론 통계(Inferential Statistics)
       • 기술 통계: 주어진 데이터의 분포나 빈도, 평균 등의 통계량을 통해서 데이터를 ‘설명’.
       • 추론 통계: 모집단을 전부 다 보기 힘드니, 샘플을 통해서 모집단을 추정하는 방식을 추론 통계라고 한다.
   • Notation
   • Key Question

3. Statistics | [핵심 확률/통계] 조건부 확률 (Conditional Probability)
   • Keyword & Implication
     • 조건부 확률 : F라는 사건이 일어났다는 조건 하에 E가 일어날 확률.
     • 확률의 곱셈 규칙 : notation 2번째 참고.
     • 베이즈 룰: 상호 배타적이며 합하면 S가 되는 $A_1, A_2, A_3$ 사건에 대해, 만약 B라는 이벤트가 $A_1, A_2, A_3$에 모두 걸쳐져 있다면, P(B)는 각각의 조건부 확률의 합으로 표현된다. (Law of total Probability)
       • 사전확률(Prior P), 사전정보 조건부 확률(Data P), 사후확률(Posterior P)
     • Odds : 사건 A가 발생하지 않을 경우 대비 발생할 확률.
   • Notation
     • 조건부 확률: $P(E|F) = \frac{P(EF)}{P(F)}$ for P(F) > 0
       • 매우 매우 중요함.
     • $P(A_1A_2...A_k) = P(A_1)P(A_2|A_1)P(A_3|A_1A_2)...P(A_k|A_1A_2...A_{k-1})$
       • $P(AB) = P(A)P(B|A) = P(B)P(A|B)$
         • $P(AB) = P(BA)$ 이므로. (교환법칙)
       • $P(ABC) = P(AB)P(C|AB) = P(A)P(B|A)P(C|AB)$
         • P(AB) = P(A)P(B|A) 이므로 위와 같이도 표현 가능.
     • 베이즈 룰
       • $P(B) = \sum\limits_{i=1}^nP(A_i)P(B|A_i)$
     • Odds
       • $\frac{P(A)}{P(A^c)} = \frac{P(A)}{1-P(A)}$
   • Key Question
     • 베이즈 룰 - 수업의 예제에서 (답을 안 보고) 어떤 것이 사전확률, 사전정보 조건부 확률인지를 알고 사후확률을 구할 수 있는가?
     • 독일이 우승 odds가 1/4이라면, 독일이 우승할 확률은 얼마인지 대답할 수 있나?

회고

• 오늘은 행렬/통계 쪽에서 직접 아이패드 노트에 써보면서 주로 했는데 더 재밌었다. 안다고 생각해도 내가 직접 설명하거나 쓰지 못하면 그건 그냥 모르는거다.
• 당분간은 수식/증명 등의 notaition에 있어서는 매우 부족하겠지만, 몇 달이 지나면 지금보다 더 나아져 있지 않을까! 믿고 있다ㅎㅎ