ML 04. 로지스틱 회귀

키워드

• 훈련/검증/테스트(train/validate/test) 데이터를 분리하는 이유
• 분류(classification) 문제와 회귀문제의 차이점
• 로지스틱회귀(Logistic regression)

---

• 그렇다면 데이터를 훈련/테스트 세트로 나누는 것에 더해 왜 검증세트가 필요한 것일까요?
  • 왜냐하면 훈련세트로 모델을 한 번에 완전하게 학습시키기가 어렵기 때문입니다.
  • 훈련세트로 다르게 튜닝된 여러 모델들을 학습한 후 어떤 모델이 학습이 잘 되었는지 검증하고 선택하는 과정이 필요합니다.
  • 이렇게 훈련/검증세트로 좋은 모델을 만들어 낸 후 최종적으로 테스트세트에는 단 한번의 예측테스트를 진행합니다.
  • 최종테스트 결과가 마음에 들지 않는다고 모델을 또 수정하여 테스트 세트를 더 잘 예측하는 모델을 만든다면 그 모델은 테스트세트에 과적합하여 일반화 성능이 떨어지게 될 수 있습니다.
• train set: 학습을 위한 데이터셋
• validation set : 최종 모델을 선택하는 과정에서 검증을 위한 데이터셋
• test set: 일반화 성능을 확인하기 위한 데이터셋

분류(Classfication)

타겟

• 데이터가 속할 특정 범주(확률) 예측
  • 이진분류: 타겟값이 두가지 범주인 경우( Yes or no)
  • 다중 분류: 타겟값이 세가지 이상의 범주인 경우( class 1 or 2 or …)

기준모델

• 일반적으로 가장 빈번하게 나타나는 범주(최빈 클래스, 최빈값) 설정

평가지표

• 회귀 문제의 평가지료를 사용할 수 없다.
• 정확도(accuracy)
  • 전체 예측 수에 대한 올바르게 예측한 수의 비율

Logistic Regression

선형회귀에 시그모이드(로지스틱) 함수를 씌워 특정 범주에 확률을 계산함으로써 범주 예측

• 시그모이드 함수
  

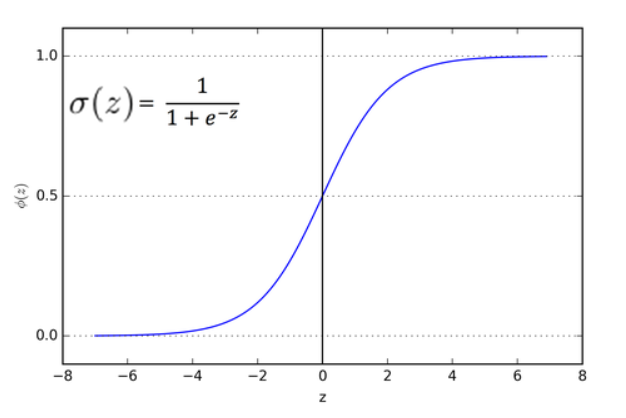
• 이렇게 오즈에 로그를 취해 변환하는 것을 로짓변환(Logit transformation)
  이라고 합니다.
• 여기서 기존 로지스틱형태의 y 값은 0~1의 범위를 가졌다면 로짓은 -∞
  ~ ∞ 범위를 가지게 됩니다.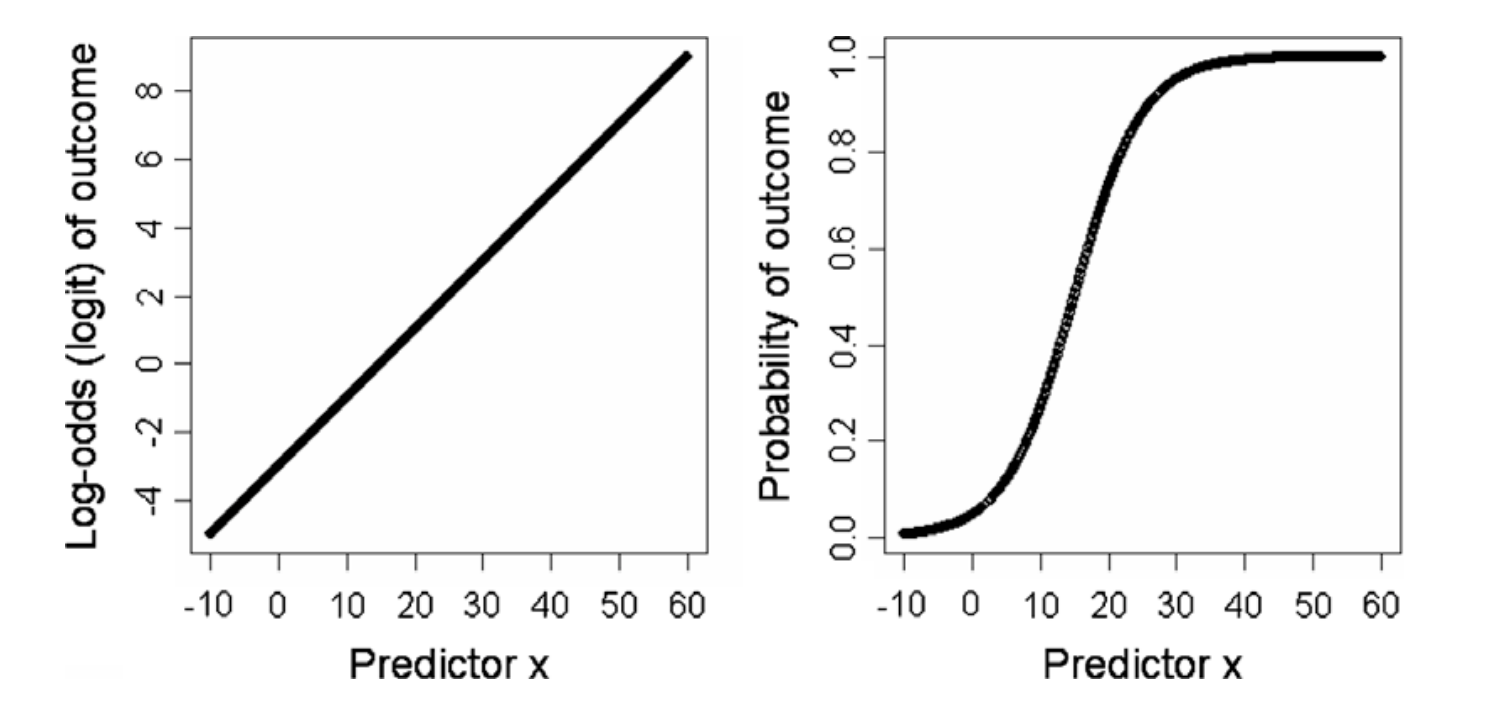

scaler 종류

1. Standard Scaler

• 기존 변수의 범위를 정규 분포로 변환하는 것.
• 데이터의 최소 최대를 모를 때 사용
• 모든 피처의 평균을 0, 분산을 1로 만듬
• 이상치가 있다면 평균과 표준편차에 영향을 미치기 때문에 데이터의 확산이 달라지게 됨
• ➡️ 이상치가 많다면 사용하지 않는 것이 좋음

2. Normalizer

• 각 변수의 값을 원점으로부터 1만큼 떨어져 있는 범위 내로 변환
• ➡️ 빠르게 학습할 수 있고 과대적합 확률을 낮출 수 있음

3. MinMaxScaler

• 데이터의 값들을 0~1 사이의 값으로 변환시키는 것
• 각 변수가 정규분포(bell-shape)가 아니거나 표준 편차가 작을 때 효과적
• BUT Standard Scaler와 같이 이상치 존재에 민감

4. Robust Scaler

• 모든 피처가 같은 크기를 갖는 다는 점이 standard와 유사
• BUT 평균과 분산이 아닌 중위수(median)과 IQR(사분위수)를 사용함
• ➡️ Standard scaler에 비해 이상치의 영향이 적어짐