코딜리티 | lesson5 - Prefix Sums : CountDiv (python)

💻lesson5 - CountDiv

1. 문제

Write a function:

def solution(A, B, K)

that, given three integers A, B and K, returns the number of integers within the range [A..B] that are divisible by K, i.e.:

{ i : A ≤ i ≤ B, i mod K = 0 }

For example, for A = 6, B = 11 and K = 2, your function should return 3, because there are three numbers divisible by 2 within the range [6..11], namely 6, 8 and 10.

Write an efficient algorithm for the following assumptions:

A and B are integers within the range [0..2,000,000,000];
K is an integer within the range [1..2,000,000,000];
A ≤ B.

2. 문제 접근

A에서 B까지 연속적인 수에서 k의 정수로 나눈 나머지가 0인 정수의 개수를 구하는 문제이다. 우선은 흔히 생각하는 방법으로 for문으로 범위를 지정한 다음 k로 나누었을때 나머지의 개수를 출력하는 방법을 사용했다.

3. 첫번째 시도 - python

def solution(A, B, K):
    cnt = 0
    for i in range(A, B+1):
        if(i%K==0):
            cnt += 1
    return cnt

4. 첫번째 결과

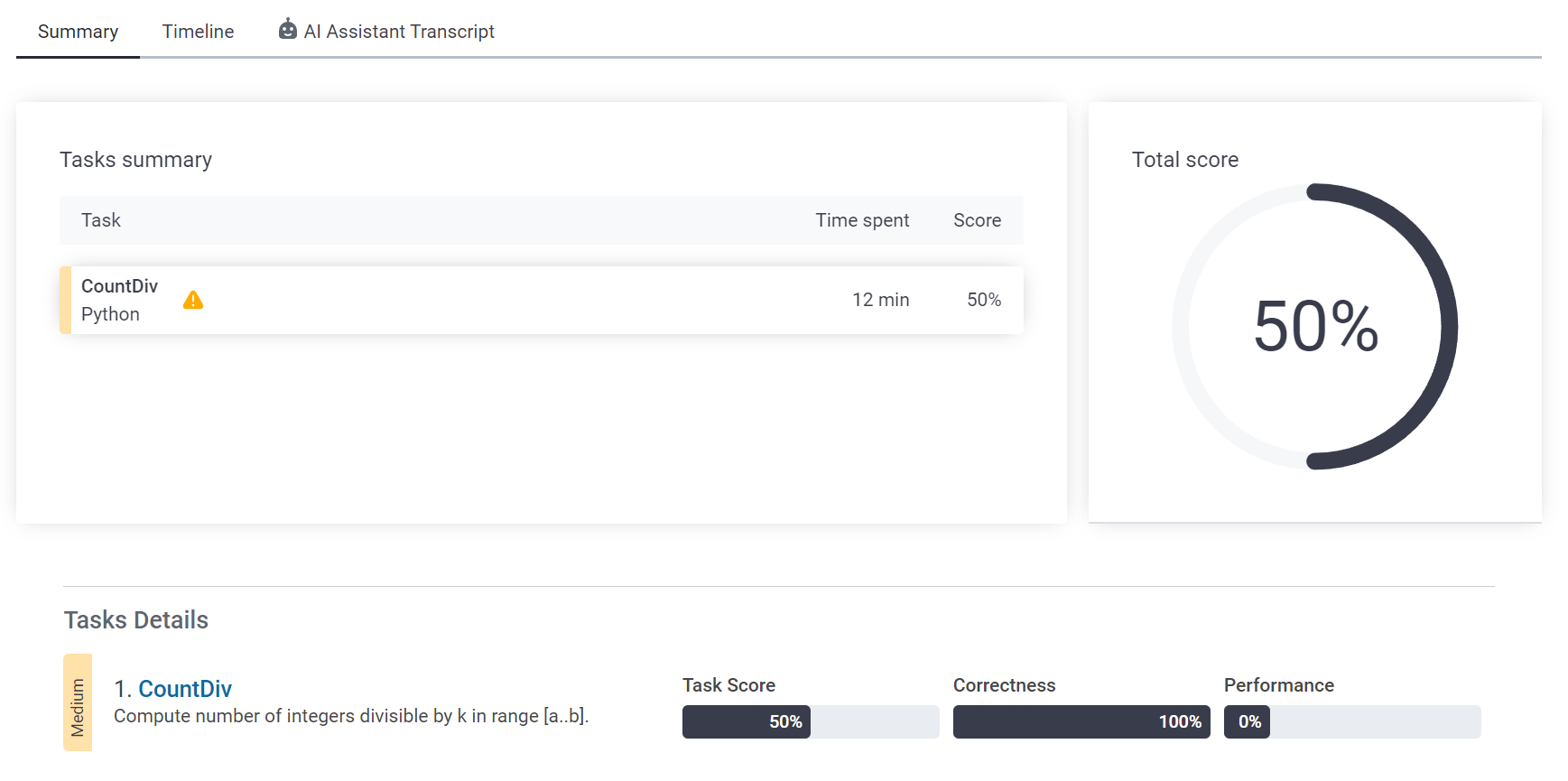
보기좋게 타임에러가 났다. 여기서보다 더 시간을 줄여야한다는 말인데...prefix라는 제목인 만큼 prefix기법을 사용해야하는 것인가보다.

5. 두번째 시도 - python

def solution(A, B, K):
    first = A + (K - A % K) % K
    last = B - (B % K)
    cnt = (last - first) // K + 1
    
    return cnt

6. 두번째 결과

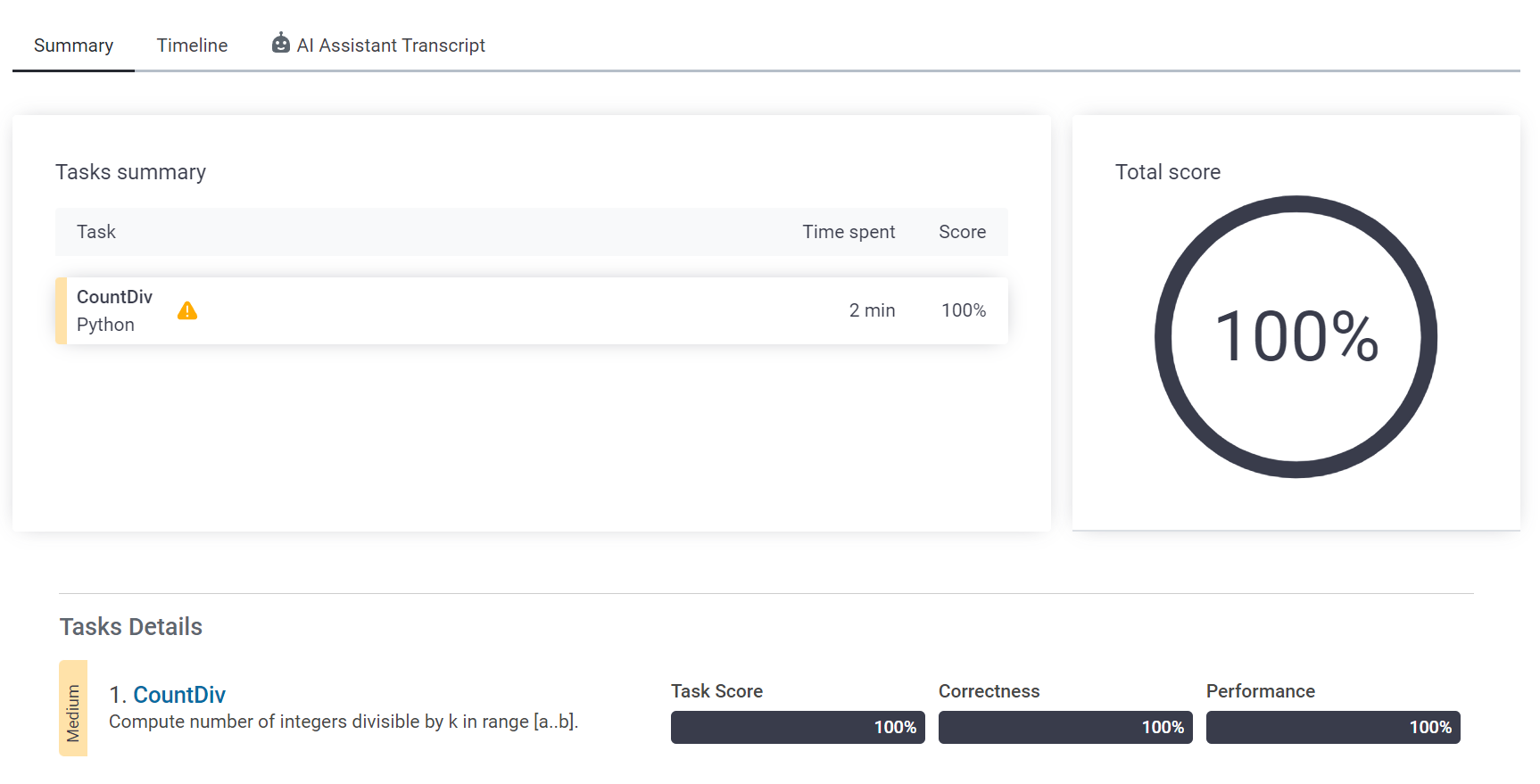
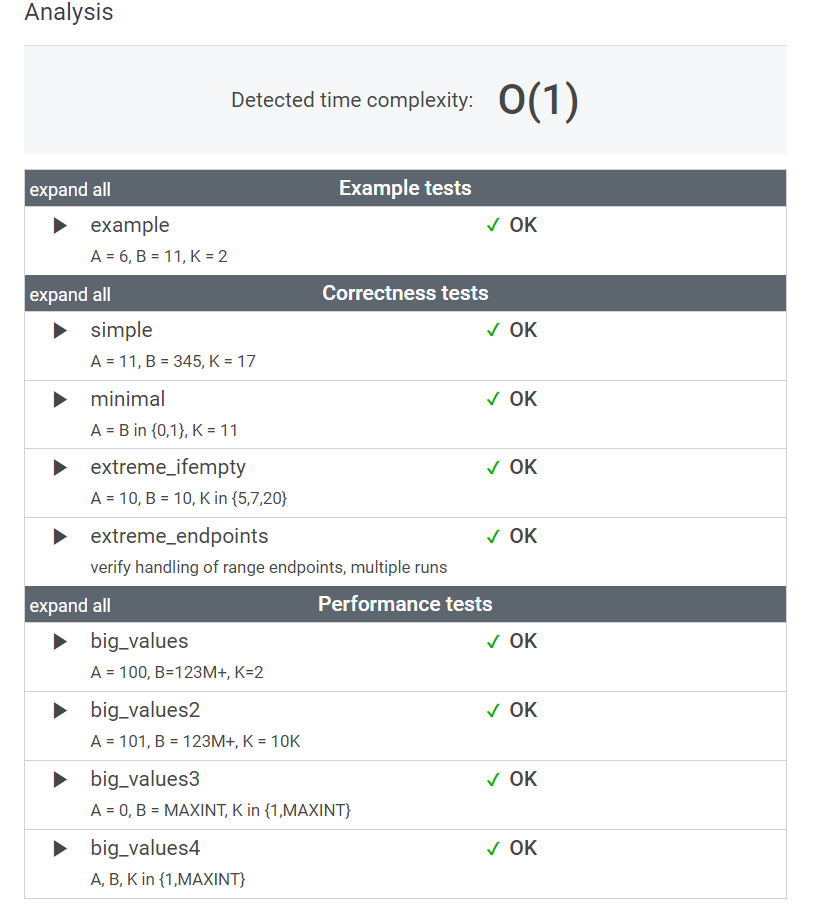
7. 마무리

같은 문제라도 다양하게 풀 수 있다는게 재밌다.