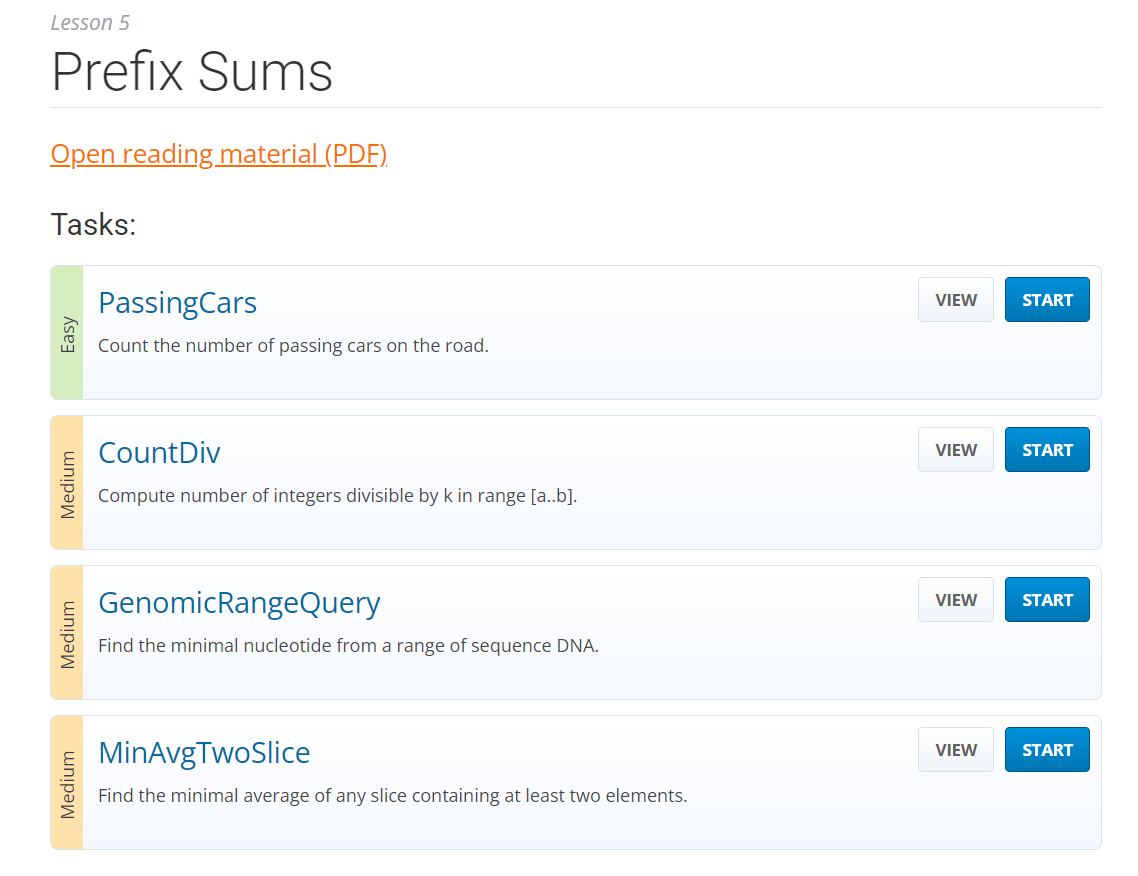
1. Prefix sums 이란?

슬라이싱된 원소의 합을 빠르게 계산할 수 있는 강력한 기술이다.
베열의 우너소를 연속적으로 총합을 내는 방법이다.

O(n)의 시간복잡도를 가짐.

def prefix_sums(A):
	n = len(A)
 	P = [0] * (n + 1)
 	for k in xrange(1, n + 1):
 	P[k] = P[k - 1] + A[k - 1]
 	return P

가장 간단한 방법은 각각의 결과를 개별적으로 전체 배열을 반복하면 되지만 이런 경우 O(n*m)의 시간복잡도가 발생하게 된다.
그렇기 때문에 슬라이스 범위에서의 원소의 총합을 구하는 것에 prefix sum은 적절한 접근일 수 있다.

2. Exercise

problem : n정수의 비어있지 않은 제로 인덱스 배열 A가 주어진다. 이 배열은 도로를 따라 연속된 지점에서 자라는 버섯의 수를 나타낸다. 또한 k, m이 주어지며 버섯을 따는 사람은 도로 k번 지점에 있으며 m개의 움직임을 수행해야한다. 한 움직임으로 그녀는 인접한 지점으로 이동한다. 그녀는 그녀가 방문하는 지점에서 자라는 모든 버섯을 수집한다. 목표는 버섯 따는 사람이 m개의 움직임으로 수집할 수 있는 최대 버섯 수를 계산하는 것이다.

Ex)

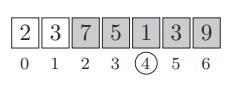
버섯 따기는 k 지점 = 4에서 시작하여 m = 6 동작을 수행해야 한다. 3, 2, 3, 4, 5, 6 지점으로 이동하여 1 + 5 + 7 + 3 + 9 = 25개의 버섯을 수집할 수 있다. 이것은 그녀가 수집할 수 있는 최대 버섯 수다.

1st solution: O(n^2)
최선의 전략은 옵션에 따라 한 방향으로 이동하는 것입니다
어떤 사람들은 반대 방향으로 움직입니다. 다시 말해서, 버섯 따는 사람이 두 번 이상 방향을 바꾸어서는 안 됩니다. 이 관찰을 통해 우리는 가장 간단한 해결책을 찾을 수 있습니다.
첫 번째 p = 0, 1, 2, ..., m이 한 방향으로 움직이게 하고, 다음 m - p가 반대 방향으로 움직이게 합니다. 이것은 O(m^2) 시간이 필요한 버섯 따기의 움직임을 단순하게 시뮬레이션한 것입니다.

2nd solution: O(n+m)
더 나은 접근법은 접두사 합을 사용하는 것입니다. 만약 우리가 한 방향으로 p이동을 하면, 우리는 버섯 따는 사람의 최대 반대 위치를 계산할 수 있습니다. 버섯 따는 사람은 이 극단들 사이의 모든 버섯을 모읍니다. 우리는 접두사 합을 사용하여 일정한 시간에 수집된 버섯의 총 수를 계산할 수 있습니다.

def mushrooms(A, k, m):
	n = len(A)
	result = 0
 	pref = prefix_sums(A)
 	for p in xrange(min(m, k) + 1):
 		left_pos = k - p
 		right_pos = min(n - 1, max(k, k + m - 2 * p))
 		result = max(result, count_total(pref, left_pos, right_pos))
 	for p in xrange(min(m + 1, n - k)):
 		right_pos = k + p
 		left_pos = max(0, min(k, k - (m - 2 * p)))
 		result = max(result, count_total(pref, left_pos, right_pos))
 	return result