문제

n개의 정점을 갖는 이진 트리의 정점에 1부터 n까지의 번호가 중복 없이 매겨져 있다. 이와 같은 이진 트리의 인오더와 포스트오더가 주어졌을 때, 프리오더를 구하는 프로그램을 작성하시오.

입력
첫째 줄에 n(1 ≤ n ≤ 100,000)이 주어진다. 다음 줄에는 인오더를 나타내는 n개의 자연수가 주어지고, 그 다음 줄에는 같은 식으로 포스트오더가 주어진다.

출력
첫째 줄에 프리오더를 출력한다.

예제 입력
3
1 2 3
1 3 2

예제 출력
2 1 3

해설

출처

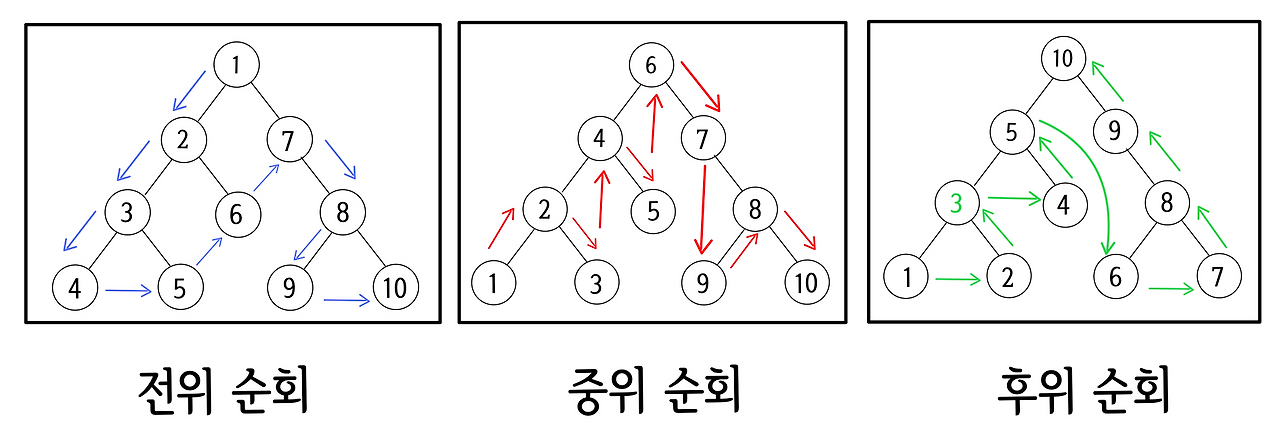
• 전위 순회 Preorder : Root - Left - Right

• 중위 순회 Inorder : Left - Root - Right

• 후위 순회 Postorder : Left - Right - Root

설계

• 후위 순회와 중위 순회가 주어졌을 때 전위 순회를 구해야 하는 상황

1. 후위 순회의 가장 마지막 원소는 현재 트리의 루트
2. 중위 순회에서는 후위 순위를 찾은 루트를 기준으로 왼쪽 서브트리 / 오른쪽 서브트리로 나뉨
3. 첫번째 루트 ➡️ 가장 큰 분기점으로 왼쪽 서브트리 / 오른쪽 서브트리 나뉨
4. 두번째 루트 ➡️ 두번째로 큰 분기점으로 첫번째 루트로 나뉜 서브트리들에서 1~2번 반복
5. N번째 루트 ➡️ N번째로 큰 분기점으로 이전에 나뉜 서브트리들에서 모두 1~2번 반복
   ➡️ 재귀

파이썬 재귀 사용 주의점

import sys
input = sys.stdin.readline

def build(il, ir, pl, pr):
    if il > ir:
        return

    root = postorder[pr]
    ans.append(root)

    idx = inorder.index(root, il, ir + 1)

    ls = idx - il

    build(il, idx - 1, pl, pl + ls - 1)
    build(idx + 1, ir, pl + ls, pr - 1)

N = int(input())
inorder = list(map(int, input().split()))
postorder = list(map(int, input().split()))

ans = []
build(0, N - 1, 0, N - 1)
print(" ".join(map(str, ans)))

• 파이썬은 기본 재귀 횟수가 1000으로 제한
• sys.setrecursionlimit(N) 을 통해 횟수 제한을 늘려줘야함
• 대부분 10^6 정도 사용하는 느낌...

시간 초과 해결

import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**6)
def build(il, ir, pl, pr):
    if il > ir:
        return

    root = postorder[pr]
    ans.append(root)

    idx = inorder.index(root, il, ir + 1)

    ls = idx - il

    build(il, idx - 1, pl, pl + ls - 1)
    build(idx + 1, ir, pl + ls, pr - 1)

N = int(input())
inorder = list(map(int, input().split()))
postorder = list(map(int, input().split()))

ans = []
build(0, N - 1, 0, N - 1)
print(" ".join(map(str, ans)))

• 재귀 해결하고 이번엔 시간 초과 발생
• root를 찾기 위해 사용한 파이썬의 arr.index()가 문제라 생각
• 직접 돌리면 빠르려나???

import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**6)
def build(il, ir, pl, pr):
    if il > ir:
        return

    root = postorder[pr]
    ans.append(root)

    idx = -1
    for k in range(il, ir + 1):
        if inorder[k] == root:
            idx = k
            break
    ls = idx - il

    build(il, idx - 1, pl, pl + ls - 1)
    build(idx + 1, ir, pl + ls, pr - 1)

N = int(input())
inorder = list(map(int, input().split()))
postorder = list(map(int, input().split()))

ans = []
build(0, N - 1, 0, N - 1)
print(" ".join(map(str, ans)))

• 똑 같 다 !
• .indx()를 사용한 이유 : 트리의 순회 문제에서는 값이 모두 다르기 때문에 가장 빠른 배열값의 인덱스를 리턴해도 괜찮다고 생각함

출처

연산	시간 복잡도	설명
len(a)	O(1)	전체 요소의 개수를 리턴
a[i]	O(1)	인덱스 i의 요소
a[i:j]	O(k)	i부터 j-1까지 슬라이싱으로 길이만큼 k개의 요소
elem in a	O(n)	elem 요소가 존재하는지 확인 / 순차 탐색 -> n만큼 시간이 소요
a.count(elem)	O(n)	elem 요소의 개수 리턴
a.index(elem)	O(n)	elem 요소의 인덱스 리턴
a.append(elem)	O(1)	리스트 마지막에 elem 추가
a.pop()	O(1)	리스트 마지막 요소를 추출
a.pop(0)	O(n)	리스트 첫번째 요소 추출 / 전체 복사 -> O(n) / Deque 사용 권장
del a[i]	O(n)	최악이 O(n) / 순차 탐색
a.sort()	O(n log n)	Tim Sort
min(a), max(a)	O(n)	전체 선형 탐색

• index()가 선형 탐색으로 O(n)
• O(1)로 해결해야 시간 초과 안난다 생각

정답 코드

import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**6)
def build(il, ir, pl, pr):
    if il > ir:
        return

    root = postorder[pr]
    ans.append(root)

    idx = pos[root]
    ls = idx - il

    build(il, idx - 1, pl, pl + ls - 1)
    build(idx + 1, ir, pl + ls, pr - 1)

N = int(input())
inorder = list(map(int, input().split()))
postorder = list(map(int, input().split()))
pos = {v: i for i, v in enumerate(inorder)}

ans = []
build(0, N - 1, 0, N - 1)
print(" ".join(map(str, ans)))

• pos = {v: i for i, v in enumerate(inorder)}
  • inorder 리스트를 처음부터 끝까지 보면서 각 값 v가 중위 순회에서 몇 번째 인덱스에 있는지를 저장
  • ex)
    inorder = [4, 2, 5, 1, 6, 3, 7]
    ➡️pos = {4: 0, 2: 1, 5: 2, 1: 3, 6: 4, 3: 5, 7:6}
• 배열 한번 돌고 인덱스 찾을 때는 O(1)