[C] 레드블랙트리(red-black tree)

레드-블랙 트리(Red-Black Tree)

자가 균형 이진 탐색 트리
대표적으로는 연관 배열 등을 구현하는데 쓰이는 자료구조이다. RB tree는 이진 트리의 특수한 형태로서, 컴퓨터 공학 분야에서 숫자 등의 비교 가능한 자료를 정리하는 데 쓰이는 자료구조이다.

레드-블랙 트리 특성

1. 모든 노드는 빨간색 혹은 검은색이다.
2. 루트 노드는 검은색이다.
3. 모든 리프 노드(NIL)들은 검은색이다.
   *NIL: null leaf, 자료를 갖지 않고 트리의 끝을 나타내는 노드
4. 빨간색 노드의 자식은 검은색이다.
   == No Double Red(빨간색 노드가 연속으로 나올 수 없다)
5. 모든 리프 노드에서 Black Depth는 같다.
   == 리프노드에서 루트 노드까지 가는 경로에서 만나는 검은색 노드의 개수가 같다.

레드-블랙 트리 삽입 과정

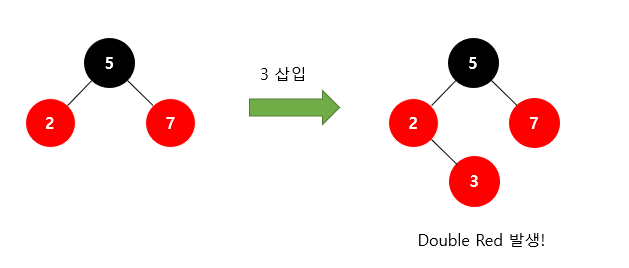
RB tree에 새로운 노드를 삽입할 때 새로운 노드는 항상 빨간색으로 삽입한다.
이렇게 되면 4번 조건이 위배되는 상황이 발생한다. 즉, 빨간색 노드가 연속으로 2번 나타날 수 있다
(Double Red)

레드 블랙 트리는 이러한 Double Red 문제를 해결하기 위해 2가지 전략을 사용한다!

새로 삽입할 노드를 N(New), 부모 노드를 P(Parent), 조상 노드를 G(Grand Parent), 삼촌 노드를 U(Uncle) 라고 하자

Double Red가 발생했을 때

• 삼촌 노드가 검은색 -> Restructuring 수행
• 삼촌 노드가 빨간색 -> Recoloring 수행

Restructuring (U : black)

Restructuring 의 과정
1. 새로운 노드(N), 부모 노드(P), 조상 노드(G)를 오름차순으로 정렬
2. 셋 중 중간값을 부모로 만들고 나머지 둘을 자식으로 만듦
3. 새로 부모가 된 노드를 검은색으로 만들고 나머지 자식들을 빨간색으로 만듦

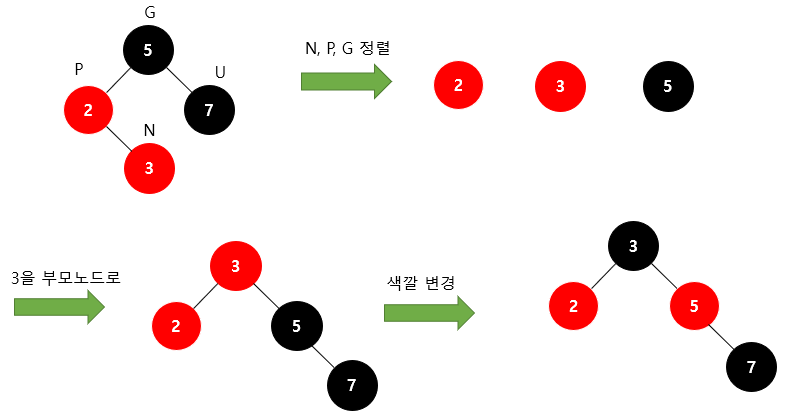
N,P,G 정렬 시 3이 중간값됨!
3을 부모 노드로 바꾸고 나머지 2와 5를 자식 노드로 바꾼다.
당연히 원래 5의 자식노드였던 7은 딸려가게 된다.
마지막으로 새롭게 부모가 된 3을 검은색으로 바꿔주고 나머지 두 자식인 2, 5의 색을 빨간색으로 바꿔주면 Double Red 문제가 해결된다.

• 여기서 규칙 3. (모든 리프노드는 검은색) 을 만족하지 않은 것처럼 보일 수 있지만, 값이 2인 노드는 자식 노드 NIL 2개를 가지고 있고 그 NIL들이 검은색이라고 생각하면 된다!

Recoloring (U : red)

Recoloring 의 과정
1. 새로운 노드(N)의 부모(P)와 삼촌(U)을 검은색으로 바꾸고 조상(G)을 빨간색으로 바꿈
1-1. 조상(G)이 루트 노드라면 검은색으로 바꿈
1-2. 조상(G)을 빨간색으로 바꿨을 때 또 다시 Double Red가 발생한다면 또 다시 Restructuring 혹은 Recoloring을 진행해서 Double Red 문제가 발생하지 않을 때까지 반복

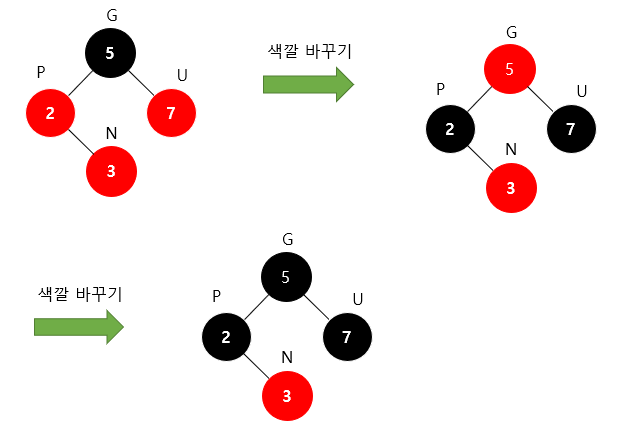
루트 노드는 검은색이라는 조건을 지켜야 하므로, 루트 노드를 검은색으로 바꾼다.
이렇게 하면 모든 조건이 지켜지면서 Double Red 문제 해결!

검은색 노드는 2번 나와도 되는가? -> Yes
빨간색 노드가 2번 나오면 안 되는 것

Recoloring은 간단해 보이지만 문제는 조상 노드(G)가 루트 노드가 아니면서, 조상 노드(G)가 또 다시 Double Red 문제가 발생하는 경우

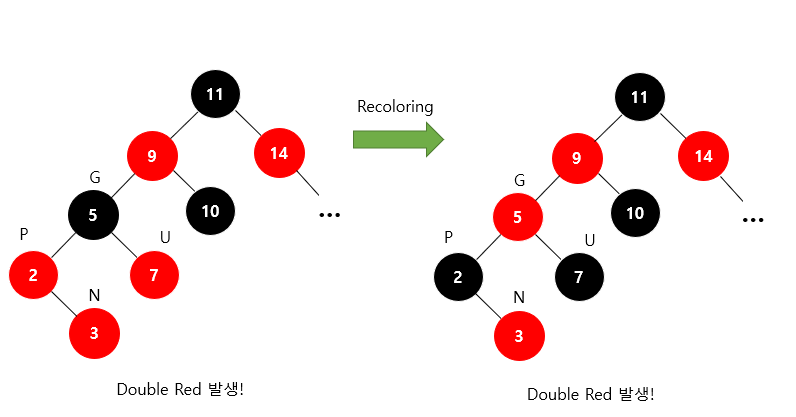
왼쪽 트리에서 recoloring을 진행하면 오른쪽 트리가 된다.
이 때 조상 노드(G)가 또 다시 Double Red..

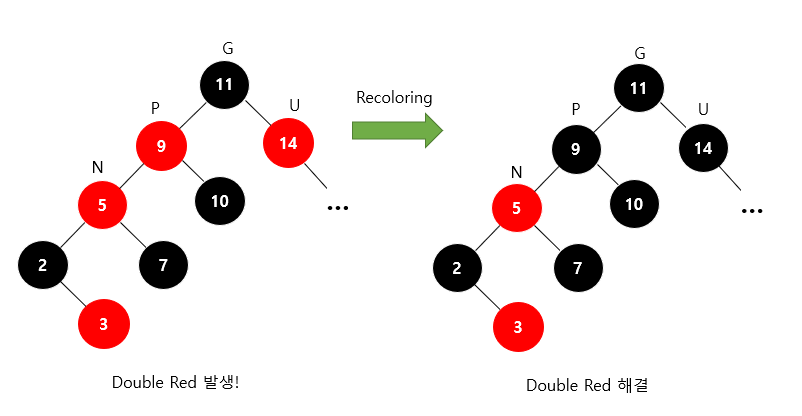
Double Red 문제가 발생한 값이 5인 노드를 기준으로 보면, 해당 노드의 삼촌(U)이 빨간색이므로 다시 recoloring을 진행해주면 Double Red 문제를 해결할 수 있다!
만약 해당 노드의 삼촌(U)이 검은색이었다면 restructuring을 진행해주면 됨

🚨 삼촌 노드가 안보일 때
맨 위의 그림을 보면 모든 리프 노드들은 검은색 NIL 노드인 것을 확인할 수 있다.
즉, 비어있는 것처럼 보이면 그냥 검은색 노드가 있다고 생각하자!

Double Red가 발생한 상황에서 부모는 보이는데, 삼촌이 안 보인다. 이때 삼촌은 NIL 노드(검은색)이다.
따라서 Restructuring을 진행하면 된다.

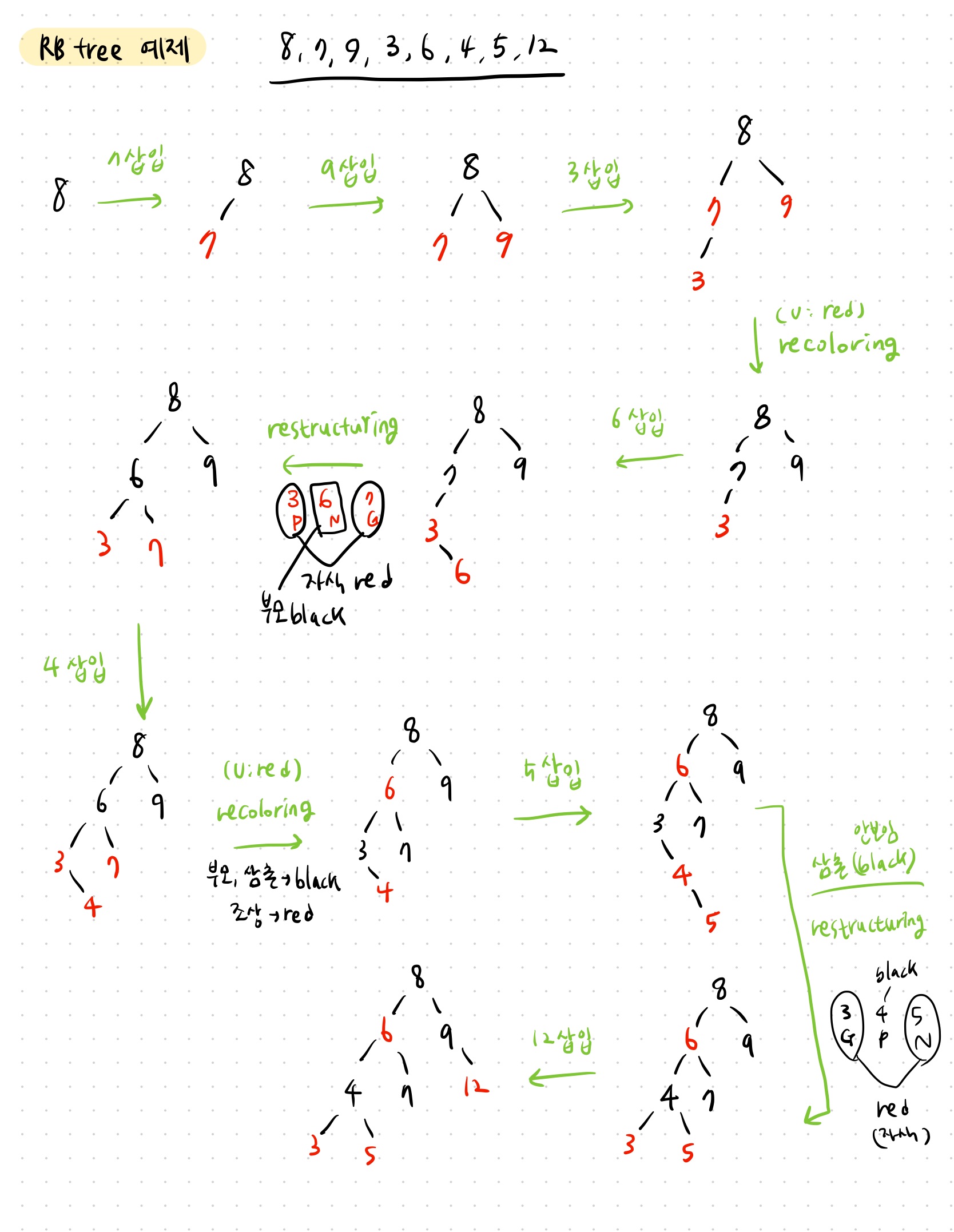
레드-블랙 트리 예제

Q. 레드-블랙 트리에 순서대로 8, 7, 9, 3, 6, 4, 5, 12를 삽입한 후의 상태를 그리시오.

레드-블랙 트리 시뮬레이터

https://www.cs.usfca.edu/~galles/visualization/RedBlack.html

레드-블랙 트리를 사용하는 이유

이진 탐색 트리의 단점을 보완하기 위해서 쓰는 자료구조
정렬된 데이터를 이진 탐색 트리로 구현하다면 아래와 같은 모습일 것이다.

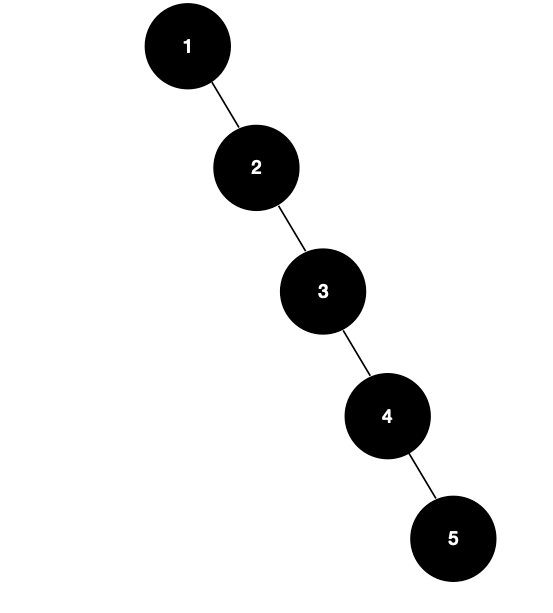
시간복잡도를 따진다면 O(n) -> 이미 정렬된 데이터에 대해서는 비효율적인 자료구조
but, RB tree의 경우, 최악의 경우에도 O(log n)의 시간복잡도로 삽입, 삭제, 검색을 할 수 있다.
이는 루트 노드부터 가장 먼 리프 노드까지의 거리가, 가장 가까운 노드 경로까지의 거리의 두 배 보다 항상 작다는 특성 때문에 성립한다.

---

참고