[Silver I] 1, 2, 3 더하기 9 - 16195

문제 링크

성능 요약

메모리: 63904 KB, 시간: 432 ms

분류

다이나믹 프로그래밍

문제 설명

정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 7가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다.

• 1+1+1+1
• 1+1+2
• 1+2+1
• 2+1+1
• 2+2
• 1+3
• 3+1

정수 n과 m이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 프로그램을 작성하시오. 단, 사용한 수의 개수는 m개 이하 이어야 한다.

입력

첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, 정수 n과 m이 주어진다. n은 양수이며 1,000보다 작거나 같다. m도 양수이며, n보다 작거나 같다.

출력

각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 1,000,000,009로 나눈 나머지를 출력한다. 단, 사용한 수의 개수는 m개 이하 이어야 한다.

---

풀이

아이디어

처음 DP라고 결정하고 문제를 풀기 시작하였다. 구하고자 하는 것이 m 이하의 수를 사용한 n 만들기인데, 따라서 필요한 변인이 2개

로 결정내리고 2차원 DP 테이블을 만들기로 했다.

또한 3까지는 미리 입력을 해야할 필요성을 가졌다. 이유는 3까지는 1가지의 숫자로도 만들 수 있는 경우가 나오지만 그를 초과하는 수는 1가지 숫자만 가지고서는 만들고자하는 수를 만들 수 없기 때문이다.

그러면 이를 넘어가는 DP테이블을 손으로 그려보자.

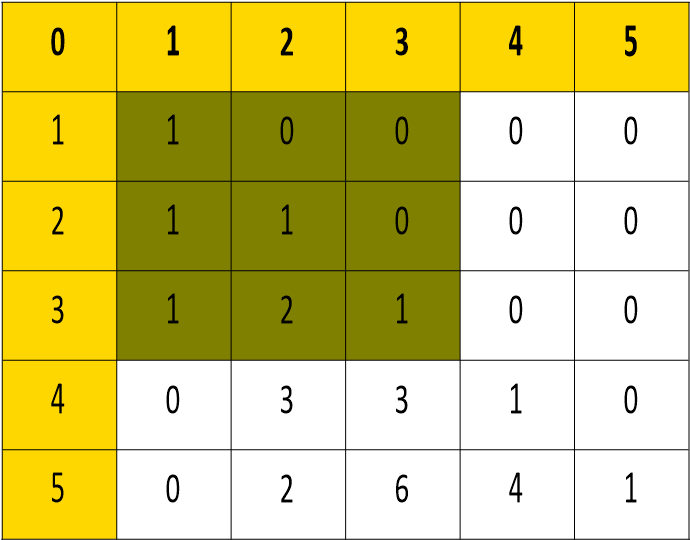
표의 세로축은 표현할 숫자, 가로축은 해당 숫자를 표현하는 1,2,3의 수 이다.
녹색으료 표시한 영역은 미리 전처리 할 영역이며, 규칙을 찾을 부분을 보자.

DP[4][2]를 예시로보면, 4를 2개의 숫자로 표현하는 방법의 수이다.
이를 표현할 수 있는 방법은 {1, 3}, {2, 2}, {3, 1}인데, 이를 조금 더 풀어서 설명하면,

• 1을 1로 표현할 수 있는 방법의 수에 3을 더한 것.
• 2를 2로 표현할 수 있는 방법의 수에 2를 더한 것.
• 3을 1로 표현할 수 있는 방법의 수에 1을 더한 것.

으로 정리할 수 있다.

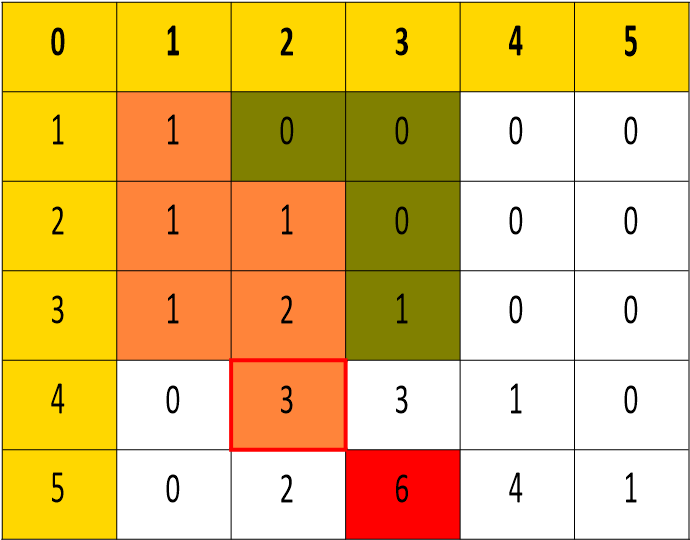
또다른 예시 하나를 더 들어보자.
DP[5][3]을 표현할 수 있는 방법은 {1, 1, 3}, {1, 3, 1}, {3, 1, 1}, {2, 2, 1}, {2, 1, 2}, {1, 2, 2} 총 6가지이다.

• 5는 4와 1의 합이며, 4를 m-1 즉, 2개로 표현할 수 있는 방법의 수는 3가지이다.
  즉 이 원리로 {1, 1, 3}, {1, 3, 1}, {1, 2, 2}를 해결할 수 있다.

• 5는 3과 2의 합이며, 3을 2개로 표현할 수 있는 방법의 수는 2가지이다.
  이를 통해 {2, 1, 2}, {2, 2, 1}을 해결할 수 있다.

• 5는 3과 2의 합이며, 2를 2개로 표현할 수 있는 방법의 수는 1가지이다.
  이를 통해 {3, 1, 1}을 해결 할 수 있다.

이를 그림으로 나타내면 아래 그림처럼 볼 수 있다.

위 규칙을 보면 점화식을 떠올릴 수 있는데 점화식은 다음과 같다

코드

dp = [[0]*1001 for _ in range(1001)]
dp[1][1] = 1
dp[2][1], dp[2][2] = 1, 1
dp[3][1], dp[3][2], dp[3][3] = 1, 2, 1

for i in range(4, 1001):
    for j in range(1, i+1):
        dp[i][j] = dp[i-1][j-1] + dp[i-2][j-1] + dp[i-3][j-1] % 1000000009

for i in range(int(input())):
    n, m = map(int, input().split())
    print(sum(dp[n][1:1+m]) % 1000000009)

---

회고

DP 골드 문제를 풀다가 약간의 벽을 느껴 실버 문제를 접한것이었는데, 아직 여기도 벽을 느끼기에는 충분한것 같다...