업데이트 예정
Outline
State: 현재 시점에서 상황이 어떤지 나타내는 값의 집합
State Space: 가능한 모든 상태의 집합
미래(S n + 1 S_{n+1} S n + 1 S n S_n S n
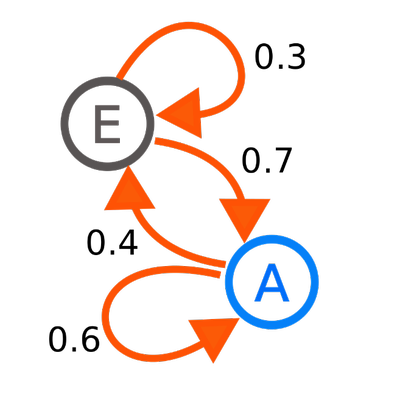
S 0 → S 1 → S 2 → . . . S n − 1 → S n → . . . 일 때 P ( S n ∣ S n − 1 ) = P ( S n ∣ S 0 , S 1 , . . . , S n + 1 ) 이다 . S_0 \rarr S_1 \rarr S_2 \rarr ...\; S_{n-1} \rarr S_n \rarr ...\;일\;때\\\;\\ P(S_n|S_{n-1})=P(S_n|S_0, S_1, ... , S_{n+1})이다. S 0 → S 1 → S 2 → . . . S n − 1 → S n → . . . 일 때 P ( S n ∣ S n − 1 ) = P ( S n ∣ S 0 , S 1 , . . . , S n + 1 ) 이 다 . 따라서 마르코프 결정 과정은 상태 집합 S S S P P P S S S S ′ S' S ′ P s s ′ P_{ss'} P s s ′
P s s ′ = P ( S t + 1 = s ′ ∣ S t = s ) P_{ss'}=P(S_{t+1}=s'|S_t=s) P s s ′ = P ( S t + 1 = s ′ ∣ S t = s ) 이때, State가 finite하다면 P P P
Markov Reward Process
보상 함수 R R R
R s = E [ R t + 1 ∣ S t = s ] R_s=E[R_{t+1}|S_t=s] R s = E [ R t + 1 ∣ S t = s ] 보상(대가, Return)는 t 시점 이후로 받는 할인률이 적용 된 모든 보상의 합입니다.
G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + ⋯ = ∑ k = 0 ∞ γ k R t + k + 1 G_t = R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\cdots=\displaystyle\sum^\infin_{k=0}\gamma^k R_{t+k+1} G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + ⋯ = k = 0 ∑ ∞ γ k R t + k + 1 여기서 할인률이란 미래에 받는 보상을 얼마나 더 가치 있게 여길 것인지를 나타내는 지표입니다.
γ ∈ [ 0 , 1 ] \gamma \in [0,1] γ ∈ [ 0 , 1 ] 위의 G t G_t G t γ \gamma γ
상태 가치 함수: 상태 s s s
V ( s ) = E [ G t ∣ S t = s ] = E [ R t + 1 + γ R t + 2 + γ 2 R t + 3 + ⋯ ∣ S t = s ] = E [ R t + 1 + γ G t + 1 ∣ S t = s ] = E [ R t + 1 + γ V ( S t + 1 ) ∣ S t = s ] = R s + γ ∑ s ′ ∈ S P s s ′ V ( s ′ ) \begin{aligned} V(s) &= E[G_t|S_t=s]\\ &=E[R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\cdots|S_t=s]\\ &=E[R_{t+1}+\gamma G_{t+1}|S_t=s]\\ &=E[R_{t+1}+\gamma V(S_{t+1})|S_t=s]\\ &=R_s+\gamma \displaystyle\sum_{s'\in S}P_{ss'}V(s') \end{aligned} V ( s ) = E [ G t ∣ S t = s ] = E [ R t + 1 + γ R t + 2 + γ 2 R t + 3 + ⋯ ∣ S t = s ] = E [ R t + 1 + γ G t + 1 ∣ S t = s ] = E [ R t + 1 + γ V ( S t + 1 ) ∣ S t = s ] = R s + γ s ′ ∈ S ∑ P s s ′ V ( s ′ ) 최종 정리 된 식을 Bellman Equation
이를 행렬로 표현하면 다음과 같습니다.
V ⃗ = R ⃗ + γ P ⃗ V ⃗ \vec V = \vec R + \gamma \vec P \vec V V = R + γ P V 이 행렬식에서 가치 함수를 계산하고자 한다면 해석적으로 다음과 같은 해를 구할 수 있습니다.
V ⃗ = ( I − γ P ) − 1 R ⃗ \vec V = (I-\gamma P)^{-1} \vec R V = ( I − γ P ) − 1 R 이 때, γ \gamma γ
Markov Decision Process
한 상태에서 다른 상태로 전이 될 때는 어떤 action을 취함으로써 전이됩니다.
상태 s s s a a a s ′ s' s ′
P s s ′ a = P ( S t + 1 = s ′ ∣ S t = s , A t = a ) P^a_{ss'} = P(S_{t+1}=s'|S_t=s, A_t=a) P s s ′ a = P ( S t + 1 = s ′ ∣ S t = s , A t = a )
상태 s s s a a a
R s a = E ( R t + 1 ∣ S t = s , A t = a ) R_s^a=E(R_{t+1}|S_t=s, A_t=a) R s a = E ( R t + 1 ∣ S t = s , A t = a )
정책(policy )는 상태 s s s a a a
π ( a ∣ s ) = P [ A t = a ∣ S t = s ] \pi(a|s)=P[A_t=a|S_t=s] π ( a ∣ s ) = P [ A t = a ∣ S t = s ]
상태 가치 함수
V π ( s ) = E π ( G t ∣ S t = s ) V_\pi(s)=E_\pi(G_t|S_t=s) V π ( s ) = E π ( G t ∣ S t = s )
상태-행동 가치 함수
q π ( s , a ) = E π ( G t ∣ S t = s , A t = a ) q_\pi(s,a) = E_\pi(G_t|S_t=s, A_t=a) q π ( s , a ) = E π ( G t ∣ S t = s , A t = a )
강화학습의 최종 목표는 최선의 정책을 찾아내는 것입니다.
{ q π ∗ = max π q π ( s , a ) V π ∗ = max π V π ( s ) \begin{cases} q_{\pi^*}=\displaystyle\max_\pi q_\pi(s,a) \\ V_{\pi^*}\;=\displaystyle\max_\pi V_\pi(s) \end{cases} ⎩ ⎪ ⎨ ⎪ ⎧ q π ∗ = π max q π ( s , a ) V π ∗ = π max V π ( s ) Bellman Expectation Equation
상태 가치 함수
V π ( s ) = E π ( G t ∣ S t = s ) = ∑ a ∈ A π ( a ∣ s ) Q π ( s , a ) = ∑ a ∈ A π ( s ∣ a ) ( R s a + γ ∑ s ′ ∈ S P s s ′ a V π ( s ′ ) ) \begin{aligned} V_\pi(s)&=E_\pi(G_t|S_t=s)\\ &=\displaystyle\sum_{a\in A}\pi(a|s)Q_\pi(s,a)\\ &=\displaystyle\sum_{a\in A}\pi(s|a)\left (R_s^a+\gamma \displaystyle\sum_{s'\in S}P_{ss'}^a V_\pi(s')\right) \end{aligned} V π ( s ) = E π ( G t ∣ S t = s ) = a ∈ A ∑ π ( a ∣ s ) Q π ( s , a ) = a ∈ A ∑ π ( s ∣ a ) ( R s a + γ s ′ ∈ S ∑ P s s ′ a V π ( s ′ ) )
상태-행동 가치 함수
q π ( s , a ) = E π ( G t ∣ S t = s , A t = a ) = R s a + γ ∑ s ′ ∈ S P s s ′ a V π ( s ′ ) = R s a + γ ∑ s ′ ∈ S P s s ′ ∑ a ′ ∈ A π ( a ′ ∣ s ′ ) q π ( s ′ , a ′ ) \begin{aligned} q_\pi(s,a) &= E_\pi(G_t|S_t=s, A_t=a)\\ &=R_s^a+\gamma \displaystyle\sum_{s'\in S}P_{ss'}^a V_\pi(s')\\ &=R_s^a+\gamma \displaystyle\sum_{s'\in S}P_{ss'}\displaystyle\sum_{a'\in A}\pi(a'|s')q_\pi(s',a') \end{aligned} q π ( s , a ) = E π ( G t ∣ S t = s , A t = a ) = R s a + γ s ′ ∈ S ∑ P s s ′ a V π ( s ′ ) = R s a + γ s ′ ∈ S ∑ P s s ′ a ′ ∈ A ∑ π ( a ′ ∣ s ′ ) q π ( s ′ , a ′ )
Optimal Policy
Optimal Value Function
{ q ∗ = max π q π ( s , a ) V ∗ = max π V π ( s ) \begin{cases} q_{*}=\displaystyle\max_\pi q_\pi(s,a) \\ V_{*}\;=\displaystyle\max_\pi V_\pi(s) \end{cases} ⎩ ⎪ ⎨ ⎪ ⎧ q ∗ = π max q π ( s , a ) V ∗ = π max V π ( s ) partial ordering on polices
모든 상태에 대해서 π \pi π μ \mu μ π \pi π μ \mu μ partial ordering 이라고 합니다.
π ≥ μ , i f V π ( s ) ≥ V μ ( s ) f o r a l l s \pi \geq \mu,\quad if\quad V_\pi(s) \geq V_\mu(s)\;for\;all\;s π ≥ μ , i f V π ( s ) ≥ V μ ( s ) f o r a l l s
MDP에는 최선의 정책 π ∗ \pi^* π ∗ π ∗ ≥ π \pi^*\geq \pi π ∗ ≥ π
{ V π ∗ = V ∗ ( s ) q π ∗ ( s , a ) = q ∗ ( s , a ) \begin{cases} V_{\pi*}=V_*(s)\\ q_{\pi^*}(s,a)=q_*(s,a) \end{cases} { V π ∗ = V ∗ ( s ) q π ∗ ( s , a ) = q ∗ ( s , a )