업데이트 예정

Value Iteration

MDP에서 살펴본 것과 같이 역행렬과 같은 해석적인 방법으로는 최적 가치 함수를 찾는 것이 어렵습니다.
그래서 가치 반복 알고리즘이라는 수치적인 방법을 사용합니다.

이를 계속 반복하게 되면 최적 상태 가치 함수에 도달 할 수 있습니다.
$\gamma<1$이면 수렴을 보장할 수 있습니다.

이 가치 반복 알고리즘을 사용한 강화학습의 일종인 Q-Learning을 쉬운 예를 통하여 배워보겠습니다.

$Greedy$ Action

만약에 우리가 Q-동네에 처음 이사를 왔고 지도가 있습니다. 음식점을 찾고 싶지만 아는 것이 하나도 없습니다. 이럴 땐 어떻게 해야 될까요?
정답은 무작정 음식점을 다녀 보는 수밖에 없습니다.

아래와 같은 경로를 통해서 음식점을 찾았습니다. 다음에도 이 음식점에 오기 위하여 기억을 하여야 합니다.
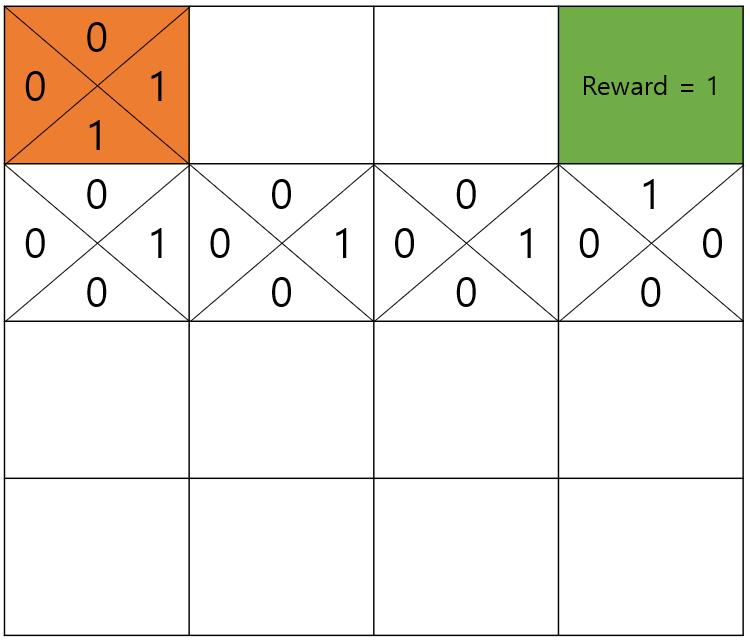
음식을 맛있게 먹고 집으로 돌아가며 각 경로에서 어떻게 움직이면 맛집을 찾을 수 있었는지 맛집의 별점을 지도에 기록을 합니다.
그러면 다음에 출발지에서 1이 써져 있는 곳으로만 이동하면 항상 1점 음식점을 찾을 수 있겠죠?

ϵ-Greedy Action

다음과 같이 알고 보니 밑에 더 맛있다는 맛집이 있다면 어떨까요?
현재의 방식으로는 맛집을 한 번이라도 찾게 된다면 그 집밖에 갈 수가 없습니다.
그래서 우리는 맛집이 어딘지 알더라도 동네를 탐험해보는 차원에서 일정 확률로 다른 곳으로 가보는 겁니다. 여기서 이 일정 확률을 $\epsilon$이라고 칭하겠습니다.

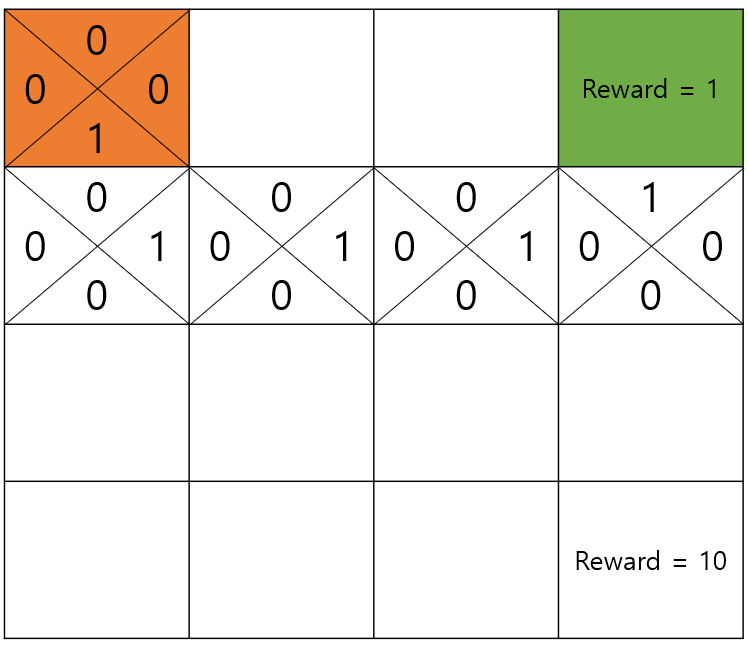
그러면 다음과 같이 다른 맛집이 어디로 가면 1점의 맛집을 갈 수 있는지, 10점의 맛집을 갈 수 있는지 알 수 있게 됩니다.

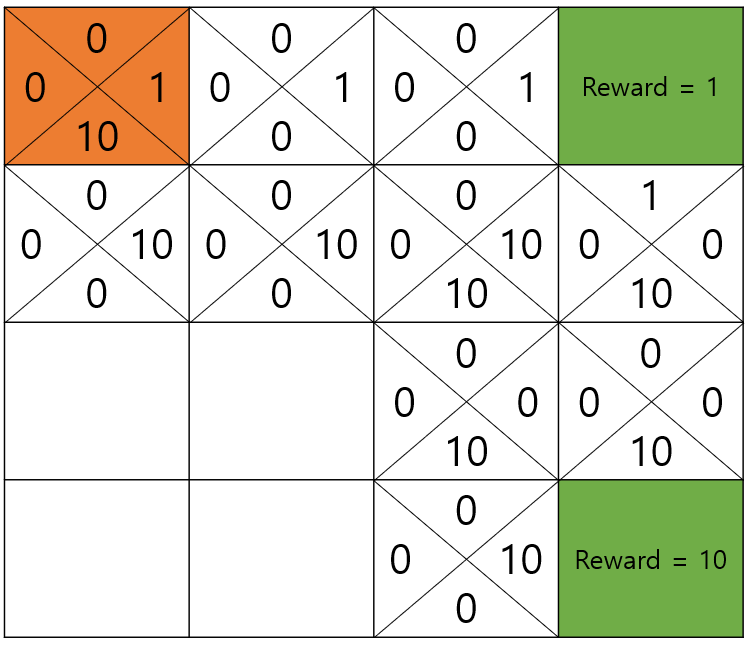
decaying ϵ-Greedy

만약 Q-동네에 10년을 살아서 모든 곳을 아는데도 탐험을 하러 다니면 안되겠죠?
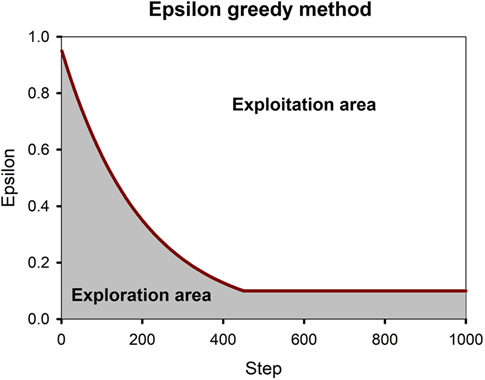
그래서 시간이 지날수록 탐험하는 시간을 점점 줄여나가야합니다.
다음과 같이 step에 따라서 $\epsilon$ 값을 점점 줄여나가는 것이 decaying $\epsilon$-Greedy입니다.

discount factor

조금 전으로 돌아가서 별점, 즉 reward가 1인 집을 가는데에는 여러가지 방법이 있습니다.
이 동네엔 하얀 배경밖에 없으니 구경할 것도 없고 굳이 돌아갈 이유가 없습니다.
그럼 빨리 가는 것이 좋은데 어디로 가는게 더 빠른지 어떻게 알 수 있을까요?

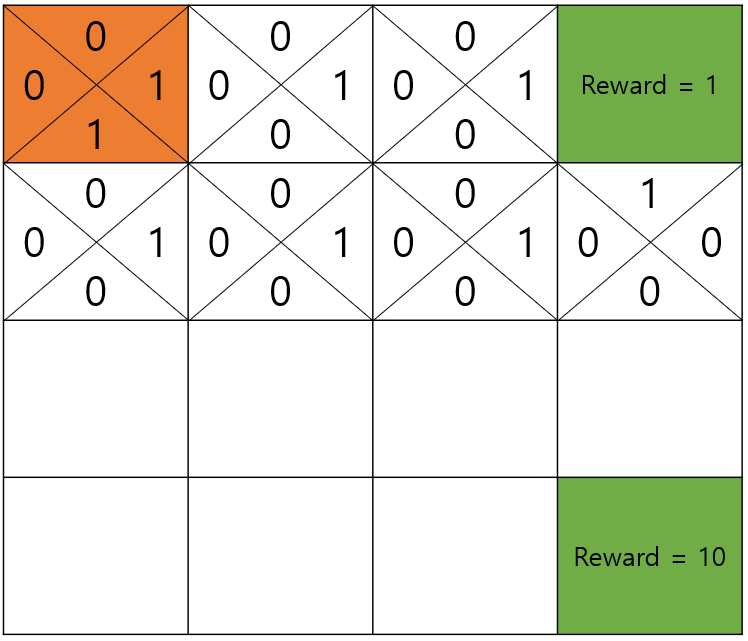
우리는 목적지부터 시작해서 집으로 돌아가면서 왔던 방향에 별점을 적어두었습니다.
별점을 그냥 적지 않고 discount factor (할인 계수)인 $\gamma$를 계속 곱하며 돌아가면 됩니다.
맛집 바로 앞의 블록은 discount factor를 적용하지 않습니다.
그러면 다음과 같이 $\gamma$가 1이 아닌 이상 최종적으로 출발지에서 더 먼길을 통하는 방향은 더 작은 값을 갖게 될 것입니다.

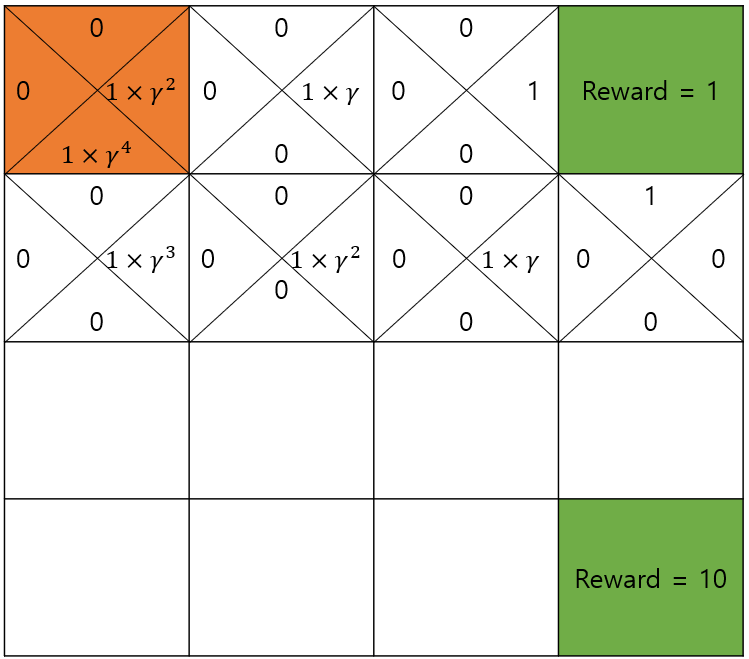
Q-Learning

지금까지 해왔던 것들은 모두 Q-Learning이라는 강화학습의 알고리즘입니다.
각각의 블럭은 하나의 state입니다.
한 state는 상하좌우, 총 4개의 action을 가집니다.
그리고 우리가 블럭마다 action 위치에 기록했던 것은 Q-Value라고 하는 행동 가치로 나타낼 수 있습니다.
다음 state의 q 가치로 이전의 q 가치를 업데이트 하는 수식은 다음과 같습니다.

1. Q 테이블을 만들고 0으로 초기화.
2. 현재 상태를 가져온다.
3. 다음을 반복한다.
   1. 행동을 한다.
   2. 보상을 받는다.
   3. 새로운 상태 관측
   4. Q 업데이트

Simulation

OpenAi의 Gym 라이브러리 중 Frozen Lake 환경을 사용한 예제입니다.

import numpy as np
import gym
import random
from gym.envs.registration import register
import matplotlib.pyplot as plt

def rargmax(v):
    m = np.amax(v) # max 함수의 별칭이다.
    indices = np.nonzero(v == m)[0] # 0이 아닌 값들을 반환한다. 행과 열 튜플이 하나씩 반환된다.
    return random.choice(indices) # 값이 같으면 랜덤으로 추출


register(
    id='FrozenLake-v3',
    entry_point='gym.envs.toy_text:FrozenLakeEnv',
    kwargs={'map_name':'4x4', 'is_slippery':False}
)
env = gym.make('FrozenLake-v3')
Q = np.zeros((env.observation_space.n, env.action_space.n))
num_episodes = 1000
dis = 0.99
alpha = 0.5
rList = []

for i in range(num_episodes):
    e = 1. / ((i / (num_episodes / 10.)) + 1)
    state = env.reset()
    rAll = 0
    done = False

    while not done:
        if np.random.rand(1) < e:
            action = env.action_space.sample()
        else:
            action = rargmax(Q[state, :])
        
        new_state, reward, done, info = env.step(action)
        if state != new_state:
            Q[state, action] = (1 - alpha) * Q[state, action] + alpha * (reward + dis * np.max(Q[new_state, :]))

        rAll += reward
        state = new_state
    rList.append(rAll)

print('Success rate: {}'.format(sum(rList)/num_episodes))
print('Final Q-Table Value')
print('LEFT DOWN RIGHT UP')
print(Q)
for i in range(4):
    print('   ', end='')
    for j in range(4): # up
        print('{:0.2f}'.format(Q[i*4+j, 3]), end='       ')
    print()
    for j in range(4):
        print('{:0.2f}'.format(Q[i*4+j, 0]), end=' ')
        print('{:0.2f}'.format(Q[i*4+j, 2]), end='  ')
    print('\n   ', end='')
    for j in range(4):
        print('{:0.2f}'.format(Q[i*4+j, 1]), end='       ')
    print('\n')

plt.style.use('classic')
plt.bar(range(len(rList)), rList, color='blue')

plt.show()