[코딩테스트] SWEA 2930 힙

Eugene CHOI·2021년 4월 7일
coding testheap
0

Coding Test

목록 보기
7/7

해당 문제는 SW Expert Academy의 문제로, 개인학습을 목적으로 게시합니다.

🧾 Problem

힙(Heap)은 최댓값 혹은 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 자료구조이다.

완전이진트리(Complete binary tree)를 기본으로 한 자료구조로서 다음과 같은 힙 속성(property)을 만족한다.

- A가 B의 부모노드(parent node) 이면, A의 키(key)값과 B의 키값 사이에는 항상 일정한 대소관계가 성립한다.

키값의 대소관계는 오로지 부모노드와 자식노드 간에만 성립하며, 형제노드 사이에서는 일정한 대소관계가 정해지지 않는다.

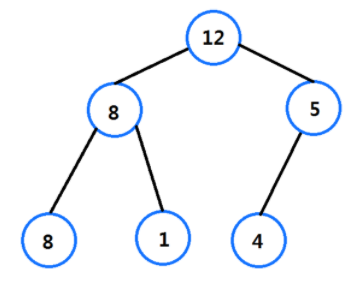
부모노드의 키값이 자식노드의 키값보다 항상 크거나 같은 힙을 '최대 힙', 부모노드의 키값이 자식노드의 키값보다 항상 작거나 같은 힙을 '최소 힙'이라고 부른다.

다음 그림은 최대 힙의 예시이다.

힙의 루트노드(root node)는 힙을 구성하는 노드의 키값 중 최댓값 혹은 최솟값을 가지게 된다.

본 문제에서는 최대 힙(max heap)을 올바르게 구현하였는지 확인할 수 있다.

초기에 최대 힙이 비어있을 때에 다음의 2가지 연산을 수행하는 프로그램을 작성하자.

연산 1. 자연수 x를 삽입

연산 2. 최대 힙의 루트 노드의 키값을 출력하고, 해당 노드를 삭제

예를 들어, 쿼리가 순서대로 다음과 같이 5개가 주어졌다고 가정해보자.

  1. 연산 1 - 3을 삽입

  2. 연산 1 - 5를 삽입

  3. 연산 2 - 최댓값 출력 후 해당 키값 삭제

  4. 연산 1 - 1을 삽입

  5. 연산 2 - 최댓값 출력 후 해당 키값 삭제

3번째 연산을 수행할 때를 기준으로 최대 키값은 5이기 때문에 5가 출력되고, 5는 삭제되기 때문에 최대 힙에는 3만 남게 된다.

5번째 연산을 수행할 때를 기준으로 최대 키값은 3이기 때문에 3이 출력되고, 3은 삭제되기 때문에 최대 힙에는 1만 남게 된다.

만약 가장 큰 키값이 여러 개일 경우에는, 삭제할 때에 그 키값을 가지는 노드들 전부가 삭제되는 것이 아니라, 루트 노드 단 하나만 삭제됨에 주의한다.

[입력]

첫 번째 줄에 테스트 케이스의 수 T가 주어진다.

각 테스트 케이스마다 첫째 줄에 수행해야하는 연산의 수를 나타내는 자연수 N(1≤N≤105)이 주어진다.

둘째 줄부터 N개의 줄에 걸쳐서 순서대로 수행해야하는 연산에 대한 정보가 주어진다.

연산 1을 수행해야 한다면 2개의 자연수 '1 x'가 주어지며, x(1≤x≤109)를 최대 힙에 추가하는 연산임을 의미한다.

연산 2를 수행해야 한다면 1개의 자연수 '2'가 주어지며, 현재 최대 힙의 루트 노드의 키값을 출력하고 해당 노드를 삭제하는 연산임을 의미한다.

[출력]

각 테스트 케이스마다 첫째 줄에 ‘#x’(x는 테스트케이스 번호를 의미하며 1부터 시작한다)를 출력하고, 연산 2의 결과들을 공백 하나를 사이에 두고 순서대로 출력한다.

만약, 연산 2를 수행해야 하는데 힙에 원소가 없어서 출력해야 할 최대 키값이 존재하지 않는다면 -1을 출력한다.

💡 Approach

이 문제는 Heap을 구현 혹은 사용하여 Heap 연산을 하고 결과를 출력하는 문제입니다.
c++의 STL에는 priorityqueue(우선순위 큐)라고 하는 최대힙 연산을 수행하는 자료구조가 존재합니다. 이 자료구조를 사용하면 쉽게 해결이 가능하겠지만, 공부를 하는 입장이니 헤더파일을 사용하지 않고 직접 구현해 봅니다.

🎄 Heap이란?

  1. Heap은 Complete Binary Tree의 일종으로 노드 중에서 값이 가장 큰 노드나 값이 가장 작은 노드를 찾기 위해서 만든 자료구조입니다.
  2. Binary Search Tree와 다르게 중복된 값을 허용하는 특징이 있습니다.
  3. for문으로 작업하면 O(n)O(n)의 시간 복잡도가 걸리지만 Heap을 이용하면 O(log⁡n)O(\log n)의 시간 복잡도를 얻을 수 있습니다.
  4. Heap은 Max Heap(최대 힙)과 Min Heap(최소 힙) 두 종류가 있습니다.
  1. Max Heap
    • 키값이 가장 큰 노드를 찾기 위한 Complete Binary Tree
    • Parent node의 key > child node의 key
    • root node: 키값이 가장 큰 노드
  2. Min Heap
    • 키값이 가장 작은 노드를 찾기 위한 Complete Binary Tree
    • Parent node의 key < child node의 key
    • root node: 키값이 가장 작은 노드

      Complete Binary Tree

      1. 마지막 level 을 제외한 나머지 level에는 빈 곳이 없이 node가 있어야 합니다.
      2. 마지막 level 에서 node 는 가장 왼쪽 부터 채워져야 합니다.

        위의 트리는 마지막 레벨을 제외한 모든 노드가 차 있고 마지막 레벨은 왼쪽부터 채워져 있으므로 Complete Binary Tree의 조건에 부합합니다. 위의 트리는 마지막 레벨의 왼쪽 노드가 비어 있기 때문에 Binary Complete Tree가 아닙니다.

🚩 Heap의 구현

Heap을 구현하는 방법에는 일반적으로 두 가지 방법이 있습니다.

  1. Linked List, 엣지가 두 개인 노드를 이용한 구현: 포인터를 이용하여 필요한 노드를 직접 heap 할당하여 만들기 때문에 메모리의 낭비를 막을 수 있습니다. 또한 포인터를 이용하므로 NULL에 대한 정의가 쉽습니다. 하지만 재귀 클래스 포인터를 이용하여 노드를 구현하기 때문에 포인터를 다루는 것이 능숙하여야 한다는 단점이 있습니다. 포인터를 잘못 다루게 되면 memory leak이 쉽게 발생하기 때문에 소멸자를 반드시 작성하는 등의 유의가 필요합니다.
    이미 2948 문자열 교집합 문제에서 했던 것처럼, left child와 right child node 포인터를 이용하여 Binary Tree를 구현하는 방법이 있습니다.

  2. Array을 이용한 구현: Complete Binary Tree는 배열을 이용하면 쉽게 구현이 가능합니다.
    • ❗ Complete Binary Tree의 경우 중간에 빈 노드가 존재하지 않습니다. 하지만 일반 Tree같은 경우에는 중간이 빈 노드가 존재할 수 있기 때문에 배열로 구현한다면, 극단적으로 skewed binary tree와 같은 경우 큰 사이즈의 배열을 필요로 하지만 대부분이 비어 있어 메모리를 심하게 낭비할 수 있습니다. 또한 복잡한 작업을 구현하려면 NULL에 대한 정의, overflow 등의 문제가 있기 때문에 쉽지 않습니다.

Array를 사용한 Heap 구현

이번 문제는 Heap이므로 간단하게 Array를 이용하여 Heap을 구현해 보겠습니다.

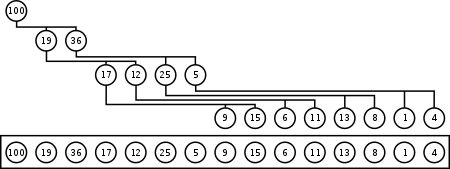
tree의 배열 다음과 같은 전제로 구현됩니다.
head의 index가 위와 같이 1부터 시작하고 레벨이 높아질수록, 또는 오른쪽으로 갈 수록 index가 커집니다.
그러면 다음과 같이 낮은 레벨 왼쪽부터 차례대로 배열에 넣을 수 있습니다.

인덱스0123456789
배열값0100193617325127


위의 배열을 보면 다음과 같은 세 가지 규칙을 가집니다.

  1. 노드 번호가 ii인 노드의 부모 노드 번호: [i/2][i/2] ([ ]:가우스 기호, 정수 내림)
  2. 노드 번호가 ii인 노드의 왼쪽 자식 노드 번호: 2∗i2∗i
  3. 노드 번호가 ii인 노드의 오른쪽 자식 노드 번호: 2∗i+12∗i+1

예를 들어 key가 17인 노드의 인덱스는 3입니다.
이 노드의 부모 노드는 19입니다. 부모 노드의 인덱스는 [3/2]=1입니다.
이 노드의 자식 노드는 9와 15입니다. 각각 3*2=6, 3*2+1=7의 인덱스를 가집니다.

Max Heap의 Push

우리는 배열을 통해 구현하기 때문에 NULL에 대한 정의가 모호합니다.
따라서 배열에 들어가는 정수는 0보다 크다는 전제로 0이 들어있는 칸은 빈 칸이라고 정의합니다.

Max Heap의 규칙은 다음과 같습니다.

  • Parent node의 key > Child node의 key
  • root node: 키값이 가장 큰 노드

Push를 한 값을 그Heap의 규칙에 맞는 노드 위치에 넣어야 합니다.
그러기 위해서는 다른 노드들과 바꿔가며 재정렬 하는 과정이 필요합니다.

  1. 일단 Heap의 마지막 빈 노드에 값을 넣습니다.
  2. 부모 노드보다 자식 노드(방금 넣은 노드) 값이 더 크다면 두 노드를 swap합니다.
  3. 부모 노드가 자식 노드보다 값이 더 작을 때까지 2번 과정을 반복합니다.
// Push할 Data 얻기
scanf("%d", &data);
// 마지막 노드 다음의 빈 자리를 현재 노드로 설정한다.
cur = ++size;
// 마지막 노드 다음의 빈 자리에 데이터를 삽입한다.
heap[cur] = data;
// 현재 노드가 1보다 크고, 현재 노드보다 부모 노드가 더 클 때까지 반복
while (cur > 1 && heap[cur] > heap[cur / 2]) {
    // 현재 노드와 부모 노드를 swap한다.
    swap(cur, cur / 2);
    // 현재 노드를 부모 노드로 업데이트한다.
    cur = cur / 2;
}

Max Heap의 Pop

Pop을 하게 되면 root node가 비게 됩니다. 하위 노드들을 모두 재정렬 하여야 합니다.

  1. root node의 값을 리턴하기 위해 저장 또는 출력해줍니다.
  2. root node와 마지막 노드를 swap하고 현재 노드를 1번 index의 노드로 설정합니다.
  3. 현재 노드가 자식 노드보다 작다면 swap 작업을 합니다.
    1. 자식 노드인 left child node와 right child node 중 큰 노드를 현재 노드와 swap합니다.
    2. 현재 노드를 바뀐 노드 위치로 업데이트 합니다.
  4. 현재 노드가 자식 노드보다 클 때까지 3번 과정을 반복합니다.
// 현재 노드를 root node로 설정한다.
cur = 1;
// 만약 노드가 하나도 없다면 음수를 반환
if (!size) printf("-1 ");
else {
    // 루트 노드의 데이터를 반환/출력
    printf("%d ", heap[cur]);
    // 루트 노드를 마지막 노드로 덮어 씌운다.
    heap[cur] = heap[size];
    // 마지막 노드를 비우고 힙의 크기를 줄인다.
    heap[size--] = 0;
    while (1) {
        // 왼쪽 자식 노드로 child 변수를 업데이트 한다.
        child = cur * 2;
        // 힙 사이즈보다 큰 인덱스를 참조하는 일이 없도록 하고,
        // 오른쪽 자식 노드가 왼쪽 자식 노드보다 크다면 child 변수를 오른쪽 자식으로 변경한다.
        if (child + 1 <= size && heap[child] < heap[child + 1]) child++;
        // 힙 사이즈보다 child 인덱스가 크거나 자식 노드가 부모 노드보다 작다면 lopo를 종료한다.
        if (child > size || heap[child] < heap[cur]) break;
        // 코드가 여기까지 온 경우, 자식 노드가 부모 노드보다 큰 경우이므로, swap해준다.
        swap(cur, child);
        // 현재 노드를 자식 노드로 업데이트한다.
        cur = child;
    }
}

Conclusion

#include <iostream>
#define MAX 100001
using namespace std;

int heap[MAX];

void swap(int i, int  j) {
    int temp = heap[i];
    heap[i] = heap[j];
    heap[j] = temp;
}

int main(int argc, char** argv)
{
    int test_case;
    int T, N, i, command, data, cur, size, child;
    scanf("%d", &T);
    for (test_case = 1; test_case <= T; ++test_case) {
        size = 0;
        for (i = 0; i < MAX; i++) heap[i] = 0;
        
        printf("#%d ", test_case);
        scanf("%d", &N);
        for (i = 0; i < N; i++) {
            scanf("%d", &command);
            if (command == 1) {
                scanf("%d", &data);
                cur = ++size;
                heap[cur] = data;
                while (cur > 1 && heap[cur] > heap[cur / 2]) {
                    swap(cur, cur / 2);
                    cur = cur / 2;
                }
            }
            else if (command == 2) {
                cur = 1;
                if (!size) printf("-1 ");
                else {
                    printf("%d ", heap[cur]);
                    heap[cur] = heap[size];
                    heap[size--] = 0;
                    
                    while (1) {
                        child = cur * 2;
                        if (child+1 <= size && heap[child] < heap[child+1]) child++;
                        if (child > size || heap[child] < heap[cur]) break;
                        swap(cur, child);
                        cur = child;
                    }
                }
            }
        }
        printf("\n");
    }
    return 0;
}
profile
Eugene CHOI
Hi, my name is Eugene CHOI the Automotive MCU FW developer.
이전 포스트

[코딩테스트] SWEA 11285 다트 게임

0개의 댓글