Variable
미분을 자동으로 계산하는 것을 코드로 구현한다는 것
그 계산의 미분을 컴퓨터가 자동으로 계산해 주는 시스템.
class Variable:
def __init__ (self, data):
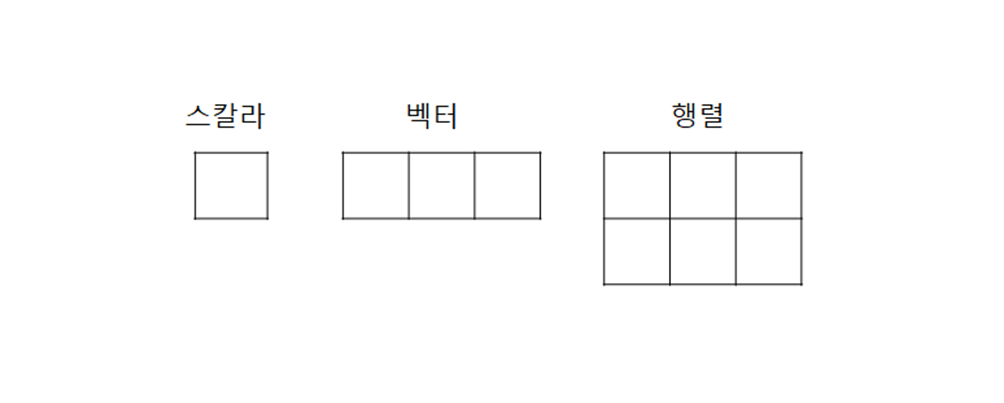
self.data = data- ML system 의 기본 데이터 구조로 '다차원 배열' 을 사용한다.
import numpy as np
data = np.array(10.0)
x = Variable(data)
print(x.data) # 10.0- 다차원 배열을 Tensor 라고 한다.
x = np.array(1)
print(x.ndim) # ()
print(x.shape) # 0
x = np.array([1, 2, 3])
print(x.ndim) # 1
print(x.shape) # (3,)
x = np.array([[1, 2, 3],
[4, 5, 6]])
print(x.ndim) # 2
print(x.shape) # (2, 3)- vector 인데, 세 개의 요소가 일렬로 늘어 있기 때문에 '3 차원 벡터' 는 벡터의 원소 수를 말한다.
np.array([1, 2, 3])Function
어떤 변수로부터 다른 변수로의 대응 관계를 정한 것.
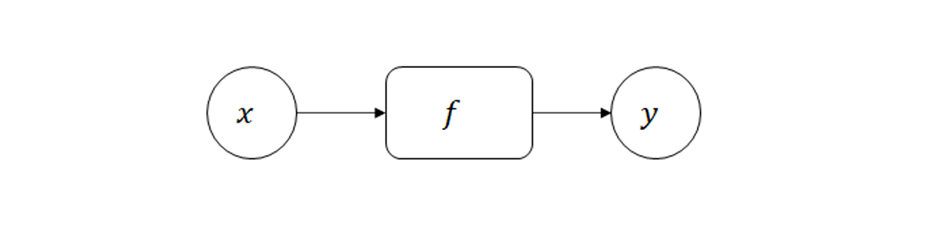
변수 그리고 함수 의 관계.
- Function 클래스는 Variable 인스턴스를 입력받아 Variable 인스턴스를 출력.
- Variable 인스턴스의 실제 데이터는 인스턴스 변수인 data 에 있다.
class Function:
def __call__(self, input): # input type is 'Variable'.
x = input.m_data
y = x ** 2
output = Variable(y)
return output
# __call__ method 는 파이썬의 특수 메서드. 이 메서드를 정의하면
# f = Function() 형태로 함수의 인스턴스를 변수 f 에 대입해두고,
# 나중에 f(...) 형태로 __call__ 메서드를 호출 할 수 있다.이 Function Class 는 'Square' 가 더 어울린다. 일단 여기서는 킵 해두고 ... 밑에서 일반화.
class Function:
def __call__(self, input):
x = input.data
y = self.forward(x)
output = Variable(y)
return output
def forward (self, x):
raise NotImplementedError()
# __call__ Method 는
# 'Variable 에서 데이터 찾기' 와 '계산 결과를 Variable 에 포장하기'
# 두 가지 일을 한다.
# raise 키워드와 현재 미구현 상태를 표현하는 NotImplementedError 를 조합하면
# 오류를 강제로 발생시킨다.forward 함수를 구현하지 않고,
class Square(Function):
def __init__(self):
pass이렇게 예외 오류를 강제로 발생 시키면,
line 16, in forward
raise NotImplementedError()
NotImplementedErrorFunction 클래스의 forward 의 Method 를 직접 호출한 사람에게 '이 메서드는 상속하여 구현해야 한다' 는 사실을 알려주게 된다.
Square function
class Square(Function):
def forward(self, x):
return x ** 2- Test code
x = Variable(np.array(10))
f = Square()
y = f(x)
print(type(y)) # <class '__main__.Variable'>
print(y.data) # 100Various Functions
Exponential function
class Exp(Function):
def forward(self, x):
return np.exp(x)- Test code
A = Square()
B = Exp()
C = Square()
x = Variable(np.array(0))
a = A(x) # x^2 = 0 (x = 0)
b = B(a) # e^a = 1 (a = 0)
y = C(b) # b^2 = 1 (b = 1)
print(y.data) # 1.0 : Variable instance
Function class 의 __call__ method 의 입 출력이 Variable instance 로 통일되어 있기 때문에 여러 함수를 연속적으로 적용 가능.

- composite function
- 계산 그래프를 이용하면, 각 변수에 대한 미분을 효율적으로 계산 가능.
- 변수 별 미분을 계산하는 알고리즘이 바로 backward propagation.
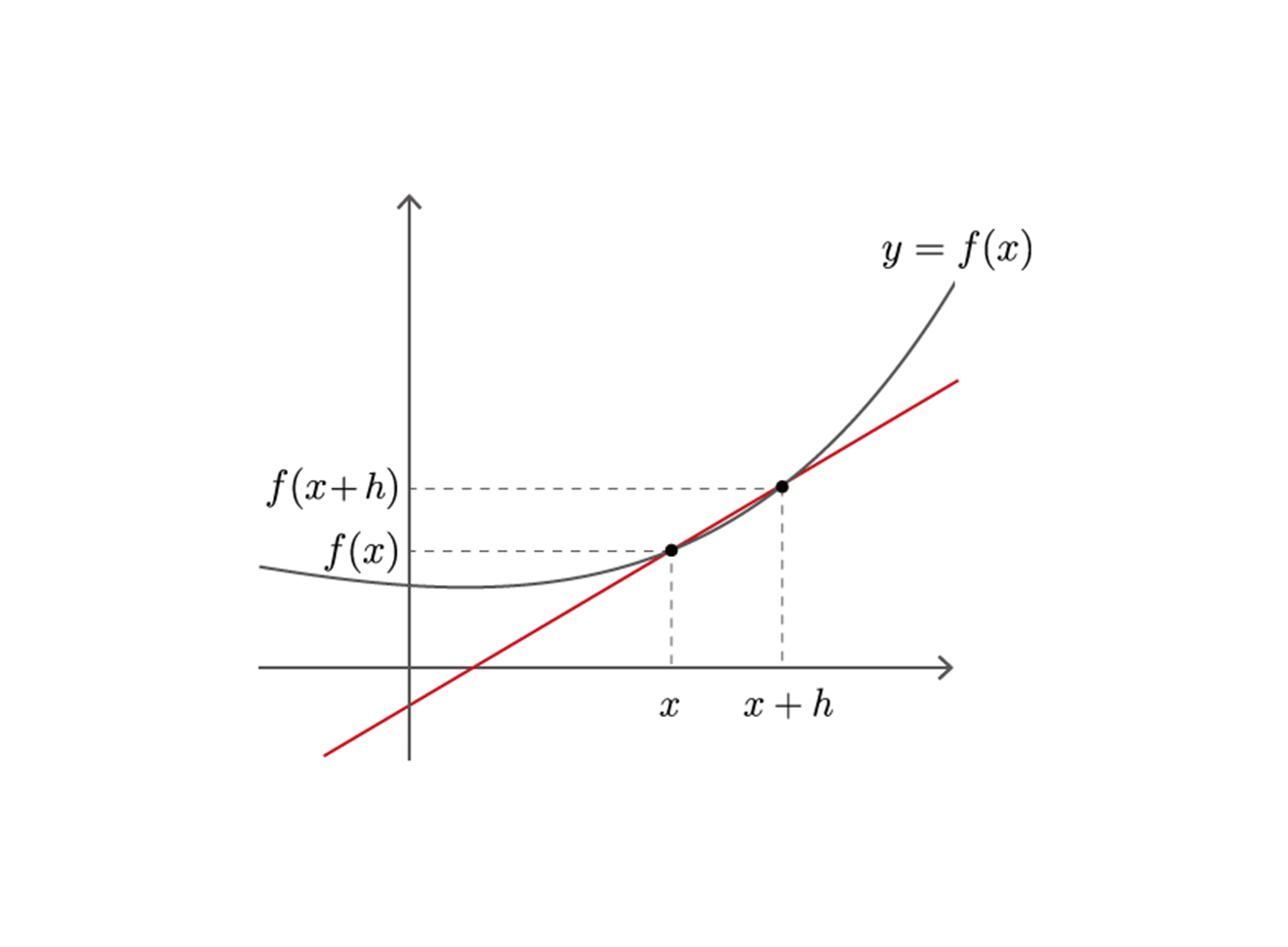
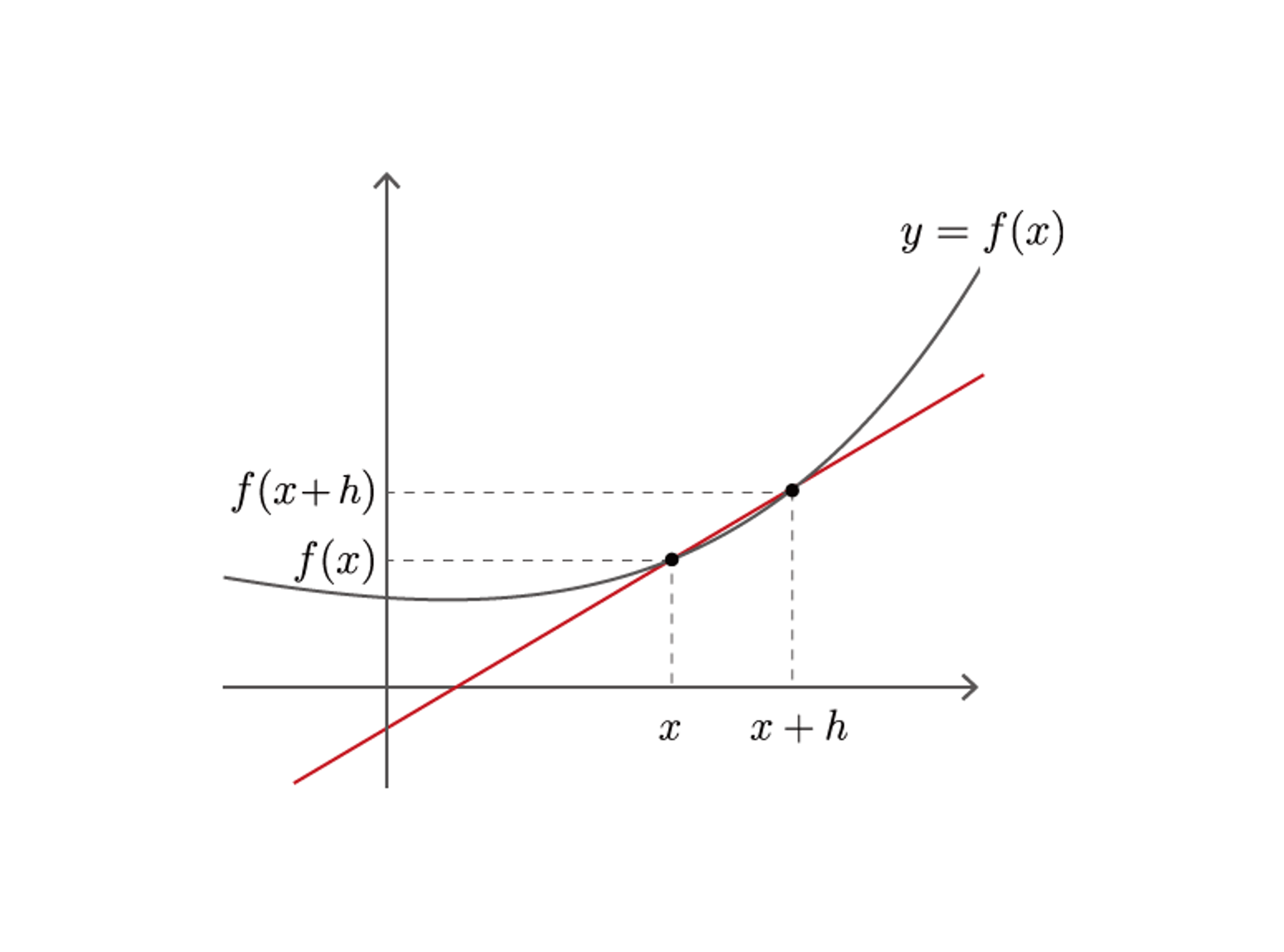
Numeric Differentiation
Variable class 와 Function class 를 구현, 미분을 자동으로 계산하기 위해 수치 미분 이라는 간단한 방법으로 계산.
미분이란 기울기, 변화율을 말한다.
- 물체의 시간에 따른 위치 변화율 ( 위치의 미분 ) 은 속도가 된다.
- 시간에 대한 속도 변화율 ( 속도의 미분 ) 은 가속도에 해당한다.
정확한 정의는 '극한으로 짧은 시간 (순간)' 에서의 변화량.