divergence in computation.

Activation 에 대한 고찰

Activation function 을 따로 정의해서 사용할 경우.

Ex > Sigmoid

우리가 많이 봐왔던 식이고, 이것을 코드로 옮기면,

def sigmoid(x):
	return 1 / (1 + torch.exp(-x))

이와 같이 옮길 수 있다. 그런데, 문제가 있다. 생각해보면 간단한데, 인지하지 못했다.

어떤 구간 에서 부터 0 혹은 1 로 계속 수렴한다면 문제가 되지 않을까?

이 말은 $e^n = \infin$ 혹은 ${\rm ln\:}n = -\infin$ 이 되는 $\exist \;n$ 이 되며, 그렇게 되면 backpropagation 시 문제가 될 수 있음을 의미한다.

Error range.

• exponential

>>> torch.exp(torch.tensor([88.72283]))
tensor([3.4028e+38])
>>> torch.exp(torch.tensor([88.722839]))
tensor([inf])

• log

>>> torch.log(torch.tensor([1e-45]))
tensor([-103.2789])
>>> torch.log(torch.tensor([1e-46]))
tensor([-inf])

• define MAXLOG.

/* pytorch/aten/src/ATen/native/Math.h */

template <typename scalar_t>
static scalar_t _igam_helper_fac(scalar_t a, scalar_t x) {
  // compute x^a * exp(-a) / gamma(a)
  // corrected from (15) and (16) in [igam2] by replacing exp(x - a) with
  // exp(a - x).

  scalar_t ax, fac, res, num, numfac;
  static scalar_t MAXLOG = std::is_same<scalar_t,double>::value ?
    7.09782712893383996843E2 : 88.72283905206835;

개인적인 생각은 (뇌피셜), C 의 double type 의 형태를 python 에서는 float 으로 밖에 해석이 되지 않으므로, 88.72283 이 최선이라 생각한다.

BatchNorm 의 사용.

따라서 이와 같은 이유로 어떤 output layer (FC, Conv ... ) 에서 나온 다음 BatchNorm 으로 눌러 준 후에 Activation 을 하는 이유가 아닐까 생각 된다.

다만 BatchNorm 으로 눌러버린다면, Gaussian distribution 의 $N(0, 1)$ 로 가져가야 하므로, 반은 Position, 반은 Negative 숫자가 된다.

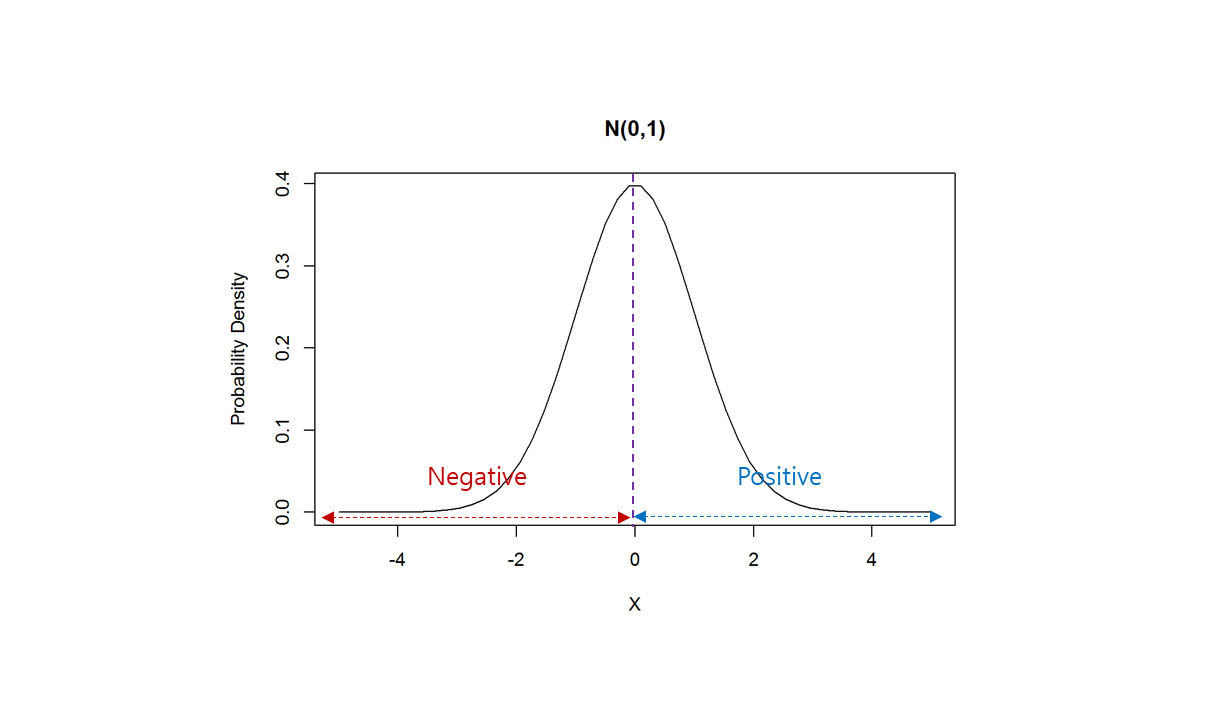
Quantized

• 실제 activation 의 sigmoid 사용 시 forward 에서 quantized 를 사용하며

# pytorch/torch/ao/nn/quantized/modules/activation.py
class Sigmoid(torch.nn.Sigmoid):
    """This is the quantized equivalent of :class:`~torch.nn.Sigmoid`.
    """
	...
    def forward(self, input):
        return torch.ops.quantized.sigmoid(input, self.output_scale, self.output_zero_point)

• pytorch 코드에서 사용하는 것을 찾아보니 output_range 로 clip 해주는 코드가 보인다.

# pytorch/test/quantization/core/test_quantized_op.py
def test_sigmoid(self, X):
    sigmoid_test_configs = [
        {
            'quantized_fn': [
                torch.ops.quantized.sigmoid
            ],
            'reference_fn': torch.sigmoid,
            'output_range': (0.0, 1.0),
            'change_zero_point': True,
            'output_is_observed': True,
        }
    ]
    self._test_activation_function(X, 'sigmoid', sigmoid_test_configs)

https://stackoverflow.com/questions/72101712/how-pytorch-implement-forward-for-a-quantized-linear-layer

quantized sigmoid 코드는 아직 못봤지만, nvidia 에서 구현된 quantized linear layer 가 있고, TensorRT 안에 tensor_quantizer.py 나 clip.py 등 꽤 흥미로운 부분이 있다.

# TensorRT/tools/pytorch-quantization/pytorch_quantization/nn/modules/quant_linear.py
...
if num_layers is None:
    self._input_quantizer = TensorQuantizer(quant_desc_input)
    self._weight_quantizer = TensorQuantizer(quant_desc_weight)

Conclusion

• Activation 을 사용하려면

1. 분포에서의 구간 CDF 등을 구하는 데이터들은 가급적 constant 로 이루어진 approximation theory (측도론, 근사 방법들) 를 이용.

   Ex > GELU (Gaussian Error Linear Unit)

2. $e^n$, ${\rm ln}\;n$ 과 같이 $\infin, -\infin$ 값이 나올 만한 데이터를 사용하려면 quantized (clip, clamp) 등을 우견하여 out_range 를 잡고 연산에 문제 없게 진행 되어야 한다.

Appendix Scalar type? (with cuda)

• PyTorch Scalar Type?

// pytorch/c10/core/ScalarType.h
// NB: Order matters for this macro; it is relied upon in
// _promoteTypesLookup and the serialization format.
#define AT_FORALL_SCALAR_TYPES_WITH_COMPLEX_AND_QINTS(_) \
  _(uint8_t, Byte) /* 0 */                               \
  _(int8_t, Char) /* 1 */                                \
  _(int16_t, Short) /* 2 */                              \
  _(int, Int) /* 3 */                                    \
  _(int64_t, Long) /* 4 */                               \
  _(at::Half, Half) /* 5 */                              \
  _(float, Float) /* 6 */                                \
  _(double, Double) /* 7 */                              \
  _(c10::complex<c10::Half>, ComplexHalf) /* 8 */        \
  _(c10::complex<float>, ComplexFloat) /* 9 */           \
  _(c10::complex<double>, ComplexDouble) /* 10 */        \
  _(bool, Bool) /* 11 */                                 \
  _(c10::qint8, QInt8) /* 12 */                          \
  _(c10::quint8, QUInt8) /* 13 */                        \
  _(c10::qint32, QInt32) /* 14 */                        \
  _(at::BFloat16, BFloat16) /* 15 */                     \
  _(c10::quint4x2, QUInt4x2) /* 16 */                    \
  _(c10::quint2x4, QUInt2x4) /* 17 */                    \
  _(c10::bits1x8, Bits1x8) /* 18 */                      \
  _(c10::bits2x4, Bits2x4) /* 19 */                      \
  _(c10::bits4x2, Bits4x2) /* 20 */                      \
  _(c10::bits8, Bits8) /* 21 */                          \
  _(c10::bits16, Bits16) /* 22 */                        \
  _(c10::Float8_e5m2, Float8_e5m2) /* 23 */              \
  _(c10::Float8_e4m3fn, Float8_e4m3fn) /* 24 */

Ex > SiLU Code

• cpu 코드

1. AT_DISPATCH_REDUCED_FLOATING_TYPES

    at::ScalarType::Half
    at::ScalarType::BFloat16

/* pytorch/aten/src/ATen/cpu/vec/functional_bfloat16.h */
	// BFloat16 specification
	template <typename scalar_t> struct VecScalarType { using type = scalar_t; };
	template <> struct VecScalarType<BFloat16> { using type = float; };
	template <> struct VecScalarType<Half> { using type = float; };

자신들이 정한 type 으로 나눈 것이고,

2. AT_DISPATCH_FLOATING_AND_COMPLEX_TYPES

	at::ScalarType::Double
    at::ScalarType::Float

float 으로 줄여 가져가는 부분이고, 연산들이 그에 맞게 casting 해서 가져가려고 한다. float 으로 downgrade 하는 느낌이 강하게 든다. 좀 더 코드를 봐야겠지만..

• Func : isReducedFloatingType.

static inline bool isReducedFloatingType(ScalarType t) {
  return t == ScalarType::Half || t == ScalarType::BFloat16 || isFloat8Type(t);
}

• Func : silu_kernel.

void silu_kernel(TensorIteratorBase& iter) {
  if (at::isReducedFloatingType(iter.dtype())) {
    AT_DISPATCH_REDUCED_FLOATING_TYPES(iter.dtype(), "silu_cpu", [&]() {
      const Vectorized<float> kOneVec(1.0f);
      cpu_kernel_vec(
          iter,
          [](scalar_t x) -> scalar_t {
            return float(x) / (1.0f + std::exp(-float(x)));
          },
          [kOneVec](Vectorized<scalar_t> x_vec) -> Vectorized<scalar_t> {
            Vectorized<float> x_vec0, x_vec1;
            std::tie(x_vec0, x_vec1) = convert_to_float<scalar_t>(x_vec);
            return convert_from_float<scalar_t>(
              x_vec0 / (kOneVec + x_vec0.neg().exp()),
              x_vec1 / (kOneVec + x_vec1.neg().exp()));
          });
    });
  } else {
    AT_DISPATCH_FLOATING_AND_COMPLEX_TYPES(
      iter.dtype(), "silu_cpu", [&]() {
        const Vectorized<scalar_t> kOneVec(scalar_t(1));
        cpu_kernel_vec(
            iter,
            [](scalar_t x) {
              return x / (scalar_t(1) + std::exp(-x));
            },
            [kOneVec](Vectorized<scalar_t> x_vec) {
              return x_vec / (kOneVec + x_vec.neg().exp());
            });
      });
    }
}

• cuda 코드 .. 모든 type 을 다 아우르는 느낌?

void silu_kernel(TensorIteratorBase& iter) {
  AT_DISPATCH_FLOATING_AND_COMPLEX_TYPES_AND2(
      at::ScalarType::Half,
      at::ScalarType::BFloat16,
      iter.dtype(),
      "silu_cuda",
      [&]() {
        gpu_kernel(iter, [] GPU_LAMBDA(scalar_t x) -> scalar_t {
          using opmath_t = at::opmath_type<scalar_t>;
          const opmath_t x_acc = static_cast<opmath_t>(x);
          return x_acc / (opmath_t(1) + ::exp(-x_acc));
        });
      });
}