DP

1. 피보나치

count = 0

def f(n):       # DP Top-down without memoization
    global count
    count += 1
    if n == 0:
        return 0
    elif n == 1:
        return 1
    return f(n-1)+f(n-2)


print(f(int(input())))
print(count)

30
832040
count : 2692537

cache = [-1] * 91   # memoization 초기 설정
cache[0] = 0
cache[1] = 1
count = 0

def f(n):       # DP Top-down with memoization
    global count
    count += 1
    if cache[n] == -1:  # calculating new fibonacci sequence
        cache[n] = f(n-1)+f(n-2)
    return cache[n]



print(f(int(input())))
print(f"count : {count}")

30
832040
count : 59

반복문

cache = [-1] * 91   # memoization 초기 설정
cache[0] = 0
cache[1] = 1

n = int(input())
for i in range(2, n+1):
    cache[i] = cache[i-1]+cache[i-2]
print(cache[n])

2. 이항계수

• bino(n,0) = 1
• bina(n,n) = 1
• bino(n,r) = bino(n-1, r-1) + bino(n-1, r)

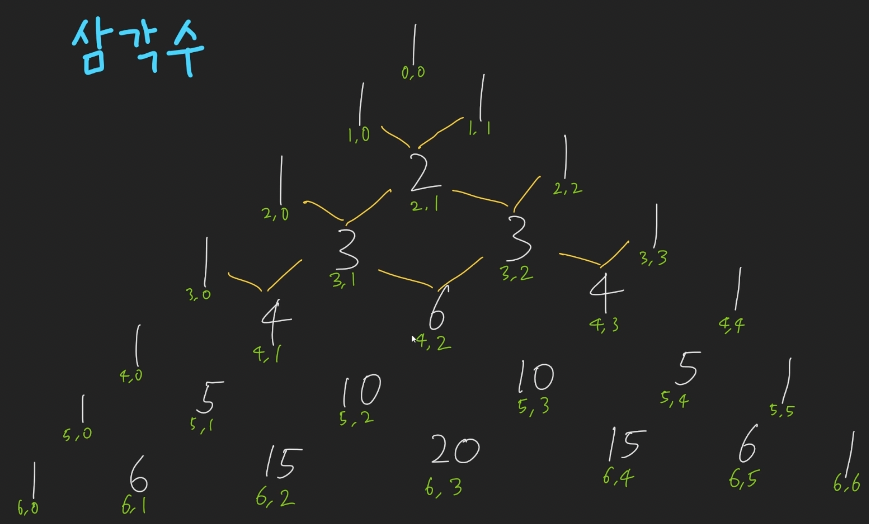
DP는 초기값과 점화식이 주어지면 이걸 Top-Down 이나 Bottom-Up 방식으로 구현을 해내면 문제를 풀수있다.
하지만 이전에 fibonacci와는 달리 전달 parameter가 하나가 아닌 2개로 늘어났다.

import sys
sys.setrecursionlimit(10**7)
input = sys.stdin.readline

mod = 10007

cache = [[0] * 1001 for _ in range(1001)]

n,k = map(int,input().split())

def bino(n,k):      # Top-down with memoization
    if cache[n][k]:
        return cache[n][k]

    if k == 0 or k == n:
        cache[n][k] = 1
    else:
        cache[n][k] = bino(n-1,k-1) + bino(n-1,k)
        cache[n][k] %= mod
    return cache[n][k]

print(bino(n,k))

# Bottom-Up
import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
mod = 10007

cache= [[0] * 1001 for _ in range(1001)]
n, k = map(int,input().split())

for i in range(1001):
    cache[i][0] = cache[i][i] = 1
    for j in range(1,i):
        cache[i][j] = cache[i-1][j-1] + cache[i-1][j]
        cache[i][j] %= mod

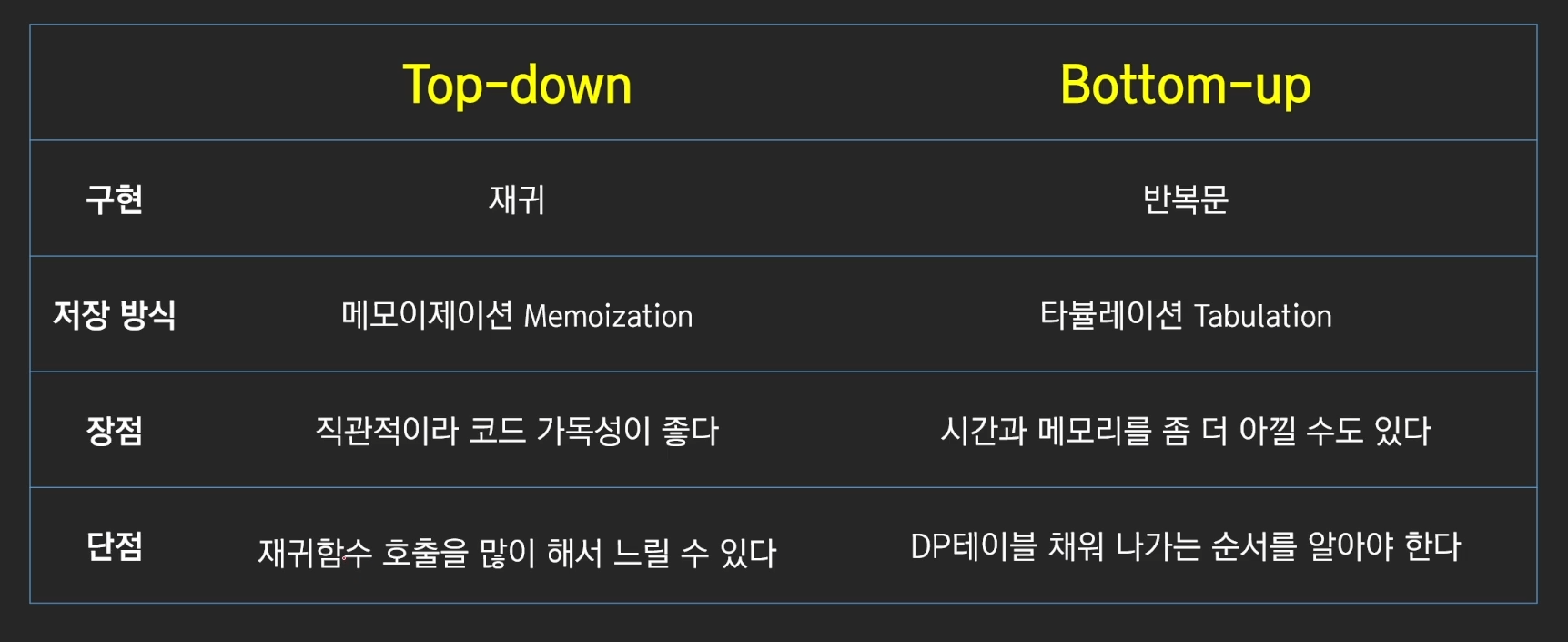
print(cache[n][k])

3. DP구현 2가지