프로그래머스 Network Delay Time

문제

문제 이해

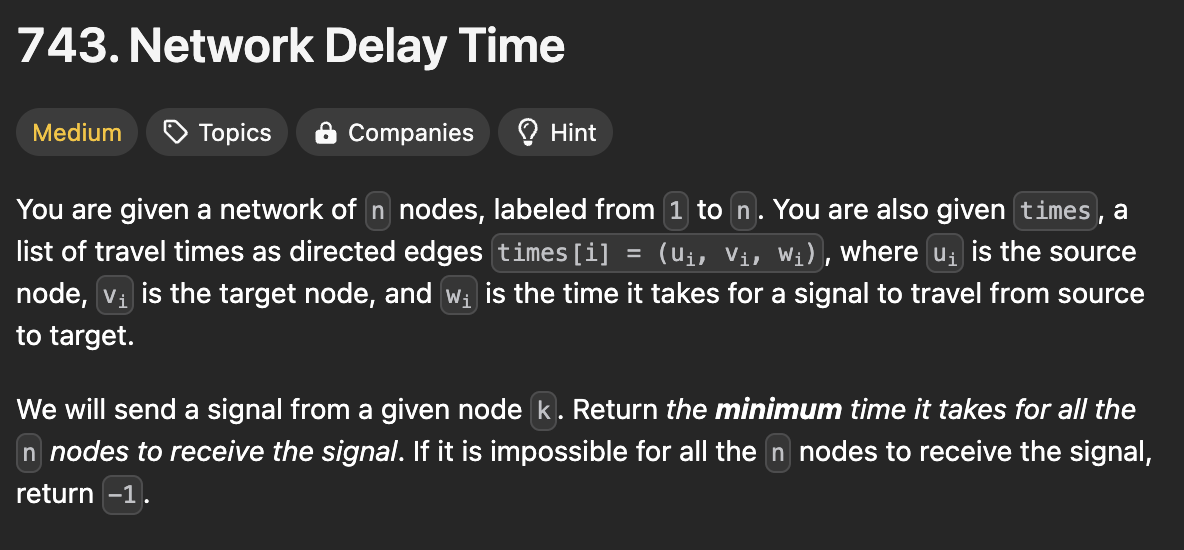
1. n노드와 간선:

• 네트워크에는 n개의 노드가 있다. 각 노드는 1부터 n까지 번호가 매겨져 있다.
• times라는 리스트는 네트워크 내에서 노드들 간의 연결 정보(간선)와 그 연결을 통해 신호가 이동하는 데 걸리는 시간을 나타낸다.
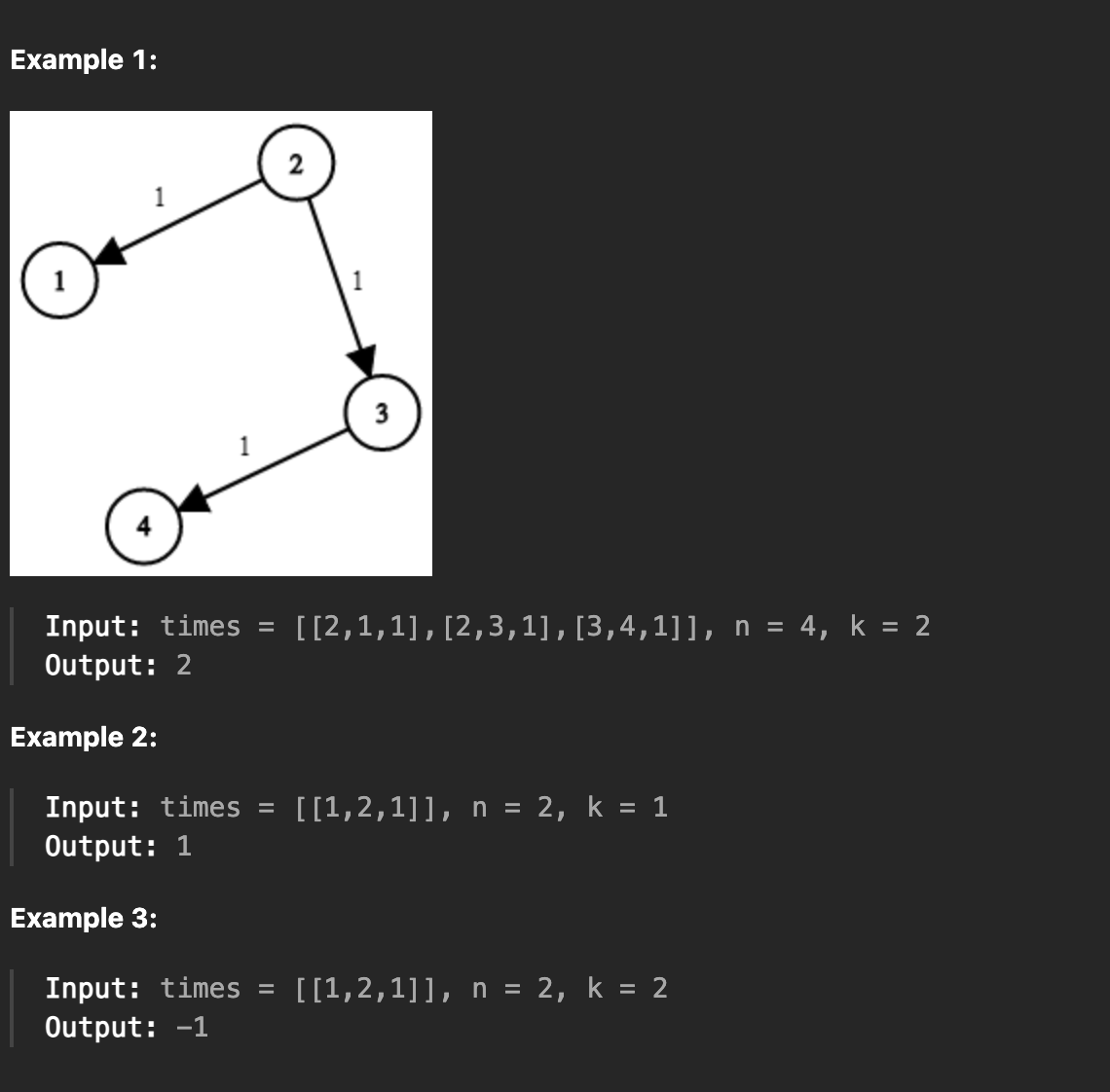
• 예를 들어, times[i] = (ui, vi, wi)는 ui번 노드에서 vi번 노드로 가는 경로가 있으며, 이 경로를 통해 신호가 전달되는 데 wi 시간이 걸린다는 의미다.

2. 신호 전송:

• 특정 노드 k에서 신호를 보낸다. 이 신호는 네트워크의 다른 노드들로 전달된다.

3. 목표:

• 모든 노드가 신호를 받을 수 있는지 확인하고, 신호가 도달하는 데 걸리는 최소 시간을 구하는 것이 목표이다.
• 만약 모든 노드가 신호를 받는 것이 불가능하다면, 즉, 어떤 노드로는 신호가 전달되지 않는다면 -1을 반환해야 한다.

정답코드

import java.util.*;

class Solution {
    public int networkDelayTime(int[][] times, int n, int k) {
        Map<Integer, List<int[]>> edges = Arrays.stream(times)
            .collect(Collectors.groupingBy(t -> t[0]));
        int[] visited = new int[n+1];
        Arrays.fill(visited, Integer.MAX_VALUE);
        Queue<int[]> pq = new PriorityQueue<>((e1, e2) -> e1[1] - e2[1]);
        pq.add(new int[]{ k, 0 });
        visited[k] = 0;

        int maxTime = 0;
        int visitCount = 1;
        while (!pq.isEmpty()) {
            int[] cur = pq.remove();
            int u = cur[0], time = cur[1];
            if (visited[u] < time) continue;
            maxTime = time;

            if (!edges.containsKey(u)) continue;
            for (int[] edge : edges.get(u)) {
                int v = edge[1], w = edge[2];
                if (time + w >= visited[v]) continue;

                if (visited[v] == Integer.MAX_VALUE) visitCount++;
                visited[v] = time + w;
                pq.add(new int[]{ v, time + w });
            }
        }

        return visitCount == n ? maxTime : -1;
    }
}

플로이드-와샬 풀이

import java.util.Arrays;

public class Solution {

    // 네트워크 지연 시간을 계산하는 메서드
    public static int networkDelayTime(int[][] times, int n, int k) {
        final int INF = Integer.MAX_VALUE; // 무한대를 나타내기 위한 값, 연결되지 않은 노드를 의미
        int[][] dist = new int[n + 1][n + 1]; // 각 노드 간의 거리를 저장할 배열, n+1 크기로 생성 (1-based 인덱스를 사용하기 위함)

        // 거리 배열을 무한대로 초기화하고, 자기 자신까지의 거리는 0으로 설정
        for (int i = 1; i <= n; i++) {
            Arrays.fill(dist[i], INF); // 모든 노드 간 거리를 INF로 초기화
            dist[i][i] = 0; // 자기 자신까지의 거리는 0으로 설정
        }

        // 입력된 간선 정보로 거리 배열을 초기화
        for (int[] time : times) {
            int u = time[0]; // 출발 노드
            int v = time[1]; // 도착 노드
            dist[u][v] = time[2]; // 해당 간선의 가중치 (시간)
        }

        // 플로이드-워셜 알고리즘을 사용하여 모든 노드 간의 최단 경로를 계산
        for (int m = 1; m <= n; m++) {  // 중간 노드로 사용될 가능성이 있는 모든 노드에 대해 반복
            for (int u = 1; u <= n; u++) { // 출발 노드
                for (int v = 1; v <= n; v++) { // 도착 노드
                    // 중간 노드를 거쳐가는 경로가 기존 경로보다 짧으면 갱신
                    if (dist[u][m] < INF && dist[m][v] < INF) {
                        dist[u][v] = Math.min(dist[u][v], dist[u][m] + dist[m][v]);
                    }
                }
            }
        }

        // 시작 노드 k에서 모든 노드까지의 최대 거리 찾기
        int maxDelay = 0; // 최대 지연 시간을 저장할 변수
        for (int j = 1; j <= n; j++) {
            if (dist[k][j] == INF) return -1; // 도달할 수 없는 노드가 있는 경우 -1 반환
            maxDelay = Math.max(maxDelay, dist[k][j]); // 최대 지연 시간 갱신
        }

        return maxDelay; // 모든 노드에 신호가 도달하는 최대 시간을 반환
    }
}