[프로그래머스/Java] Lv.0 합성수 찾기

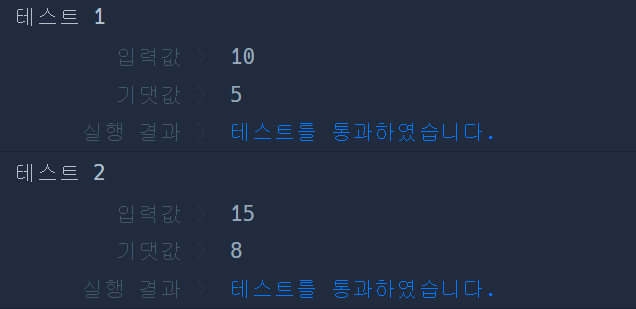
문제

약수의 개수가 세 개 이상인 수를 합성수라고 합니다. 자연수 n이 매개변수로 주어질 때 n이하의 합성수의 개수를 return하도록 solution 함수를 완성해주세요.

- 제한사항

• 1 ≤ n ≤ 100

풀이

약수의 개수를 구하는 문제는 이전에 풀어본 적이 있었다.

첫 for문은 1에서부터 n까지의 범위를 돈다. 즉 매개변수로 주어지는 n 이하의 수에서 합성수를 골라내기 위해 값을 바꿔주는 역할을 하는 것이다.

그리고 해당 for문 안에서 각 수의 약수 개수를 구해주기 위해 변수 int div를 선언하고 초기화한다. 그리고 약수를 구하기 위한 두 번째 for문을 만든다.

이때 범위는 주어진 매개변수 n의 범위가 매우 커 시간이 초과될 것을 고려해 제곱근까지만 순회하도록 하는 것이 효과적이다. 따라서 범위는 j*j <= i가 된다. 관련해 더 자세한 설명은 이전 포스팅에서 확인할 수 있다.

제곱근까지만 순회하는 과정에서, n이하의 수 i를 j로 나누었을 때 나머지가 0이 된다는 것은 j가 i의 약수라는 뜻이 된다. 따라서 개수를 +1 (div++;) 해준다. 그리고 반대의 경우를 카운트하기 위해 +1을 한 번 더 해줘야 하는데 (ex. (1, 36)과 (36,1)), 이때 변수가 되는 제곱수는 제외하기 위해 if(j != n/j)라는 조건을 추가한다. (ex. j = 6, n = 36)

이렇게 구해진 i의 약수의 개수 div가 3보다 큰 경우 합성수에 해당하므로, 변수 int cnt에 +1을 해줌으로써 n 이하의 합성수의 개수를 구할 수 있게 된다.

class Solution {
    public int solution(int n) {
        int cnt = 0;
        
        for(int i=1; i<=n; i++){
            int div = 0;
            
            for(int j=1; j*j<=i; j++){
                if(i % j == 0){
                    div++;
                    if(j != n/j) div++;
                }
            }
            
            if(div >= 3) cnt++;
        }
        
        return cnt;
    }
}

결과