1. 관련 문제 🎯
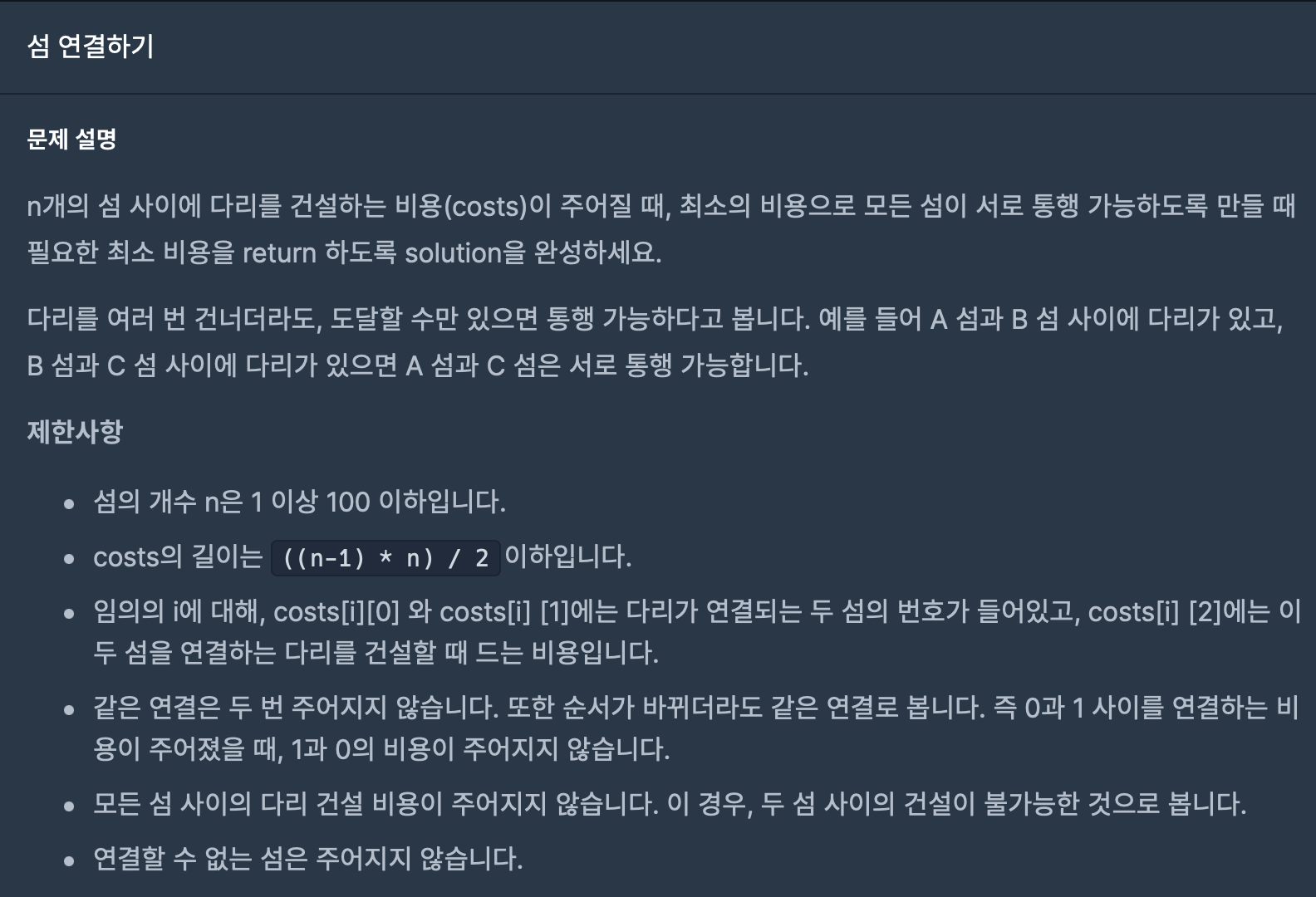
문제 : [프로그래머스] 섬 연결하기 🏝️
난이도 : LEVEL 3
2. 문제 소개 🧩
1️⃣ n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어진다.
2️⃣ 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만든다.
3️⃣ 다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다.
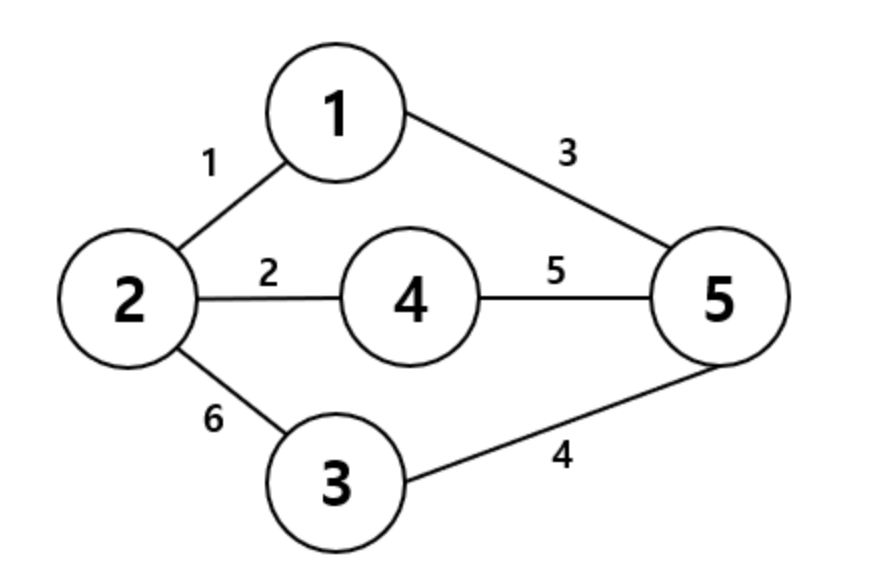
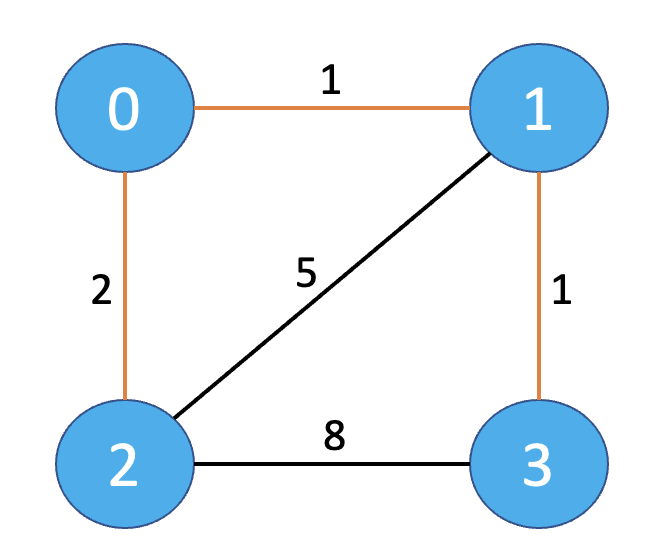
- 아래의 예시에서, 총 4개의 섬과 4개의 섬 사이에 다리를 건설하는 비용이 주어진다.
이때, 모든 섬을 서로 통행 가능하도록 하는 최소 비용은 초록색 간선인 2+1+1 = 4임을 알 수 있다.
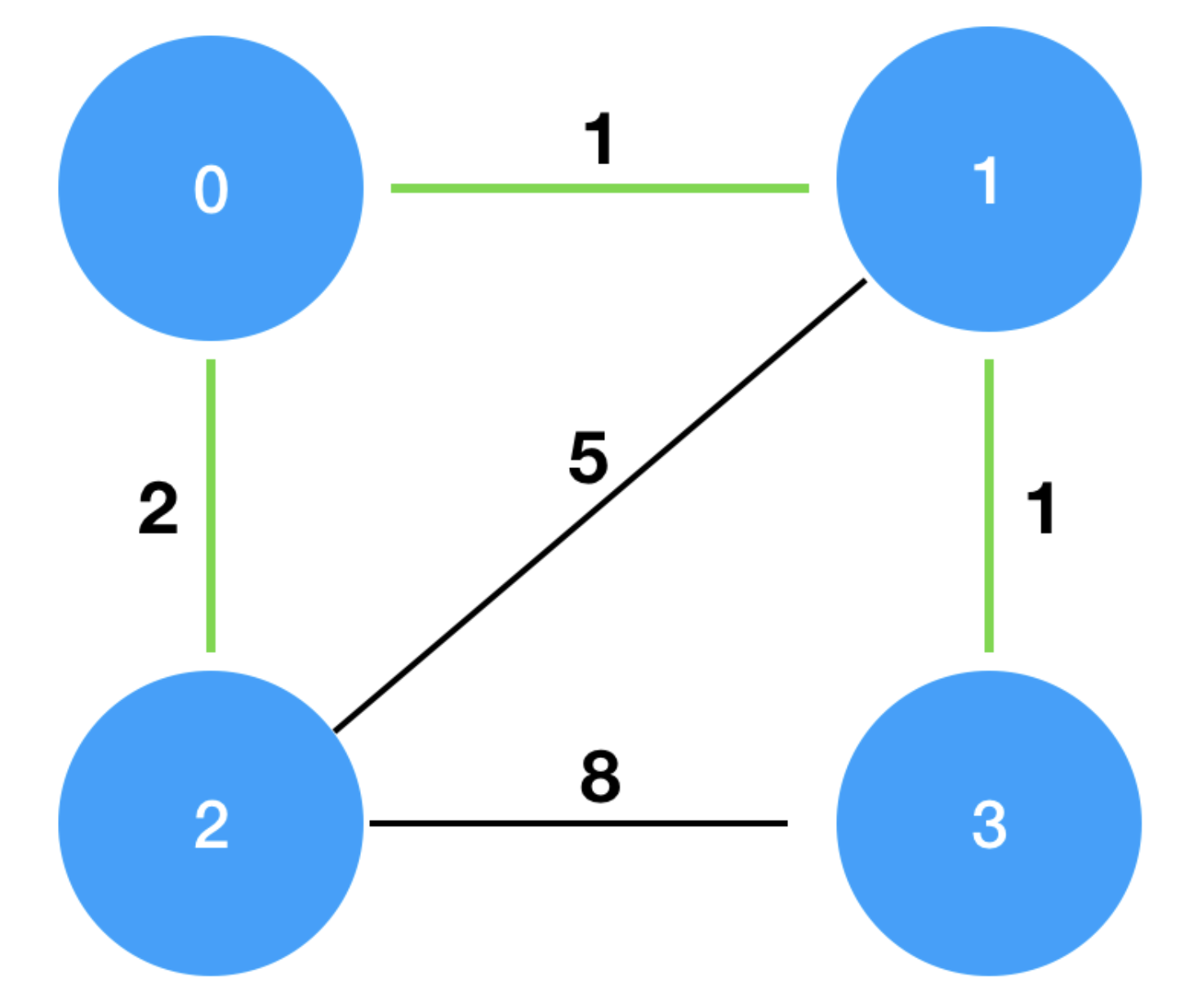
사진 출처 : https://school.programmers.co.kr/learn/courses/30/lessons/42861
3. 관련 알고리즘 소개 🖌️
🤨 여러 알고리즘을 사용해서 풀어보다가, 먼저 풀이를 보게 되었다 ㅠㅠ
이 문제는 최소 신장 트리를 구하는 '크루스칼 알고리즘'의 대표적인 문제임을 알 수 있었다!!
따라서, 해당 알고리즘에 대해서 살펴보자🧐
참고 자료 : https://chanhuiseok.github.io/posts/algo-33/
크루스칼 알고리즘이란.?
- 그래프 내의 모든 정점들을 가장 적은 비용으로 연결하기 위해 사용된다.
이때, 그래프는 정점(vertex)과 가중치가 있는 간선(edge)으로 구성되어 있다.- 그래프 내의 모든 정점을 포함하고 사이클이 없는 연결 선을 그렸을 때, 가중치의 합이 최소가 되는 상황을 구하는 경우 사용한다
- 최소 신장 트리를 구하기 위한 알고리즘이다.
신장 트리(Spannging tree)는 아래의 2가지 조건을 만족해야 한다.
- (1) 그래프의 모든 정점을 포함해야 한다.
- (2) 정점 간 서로 연결이 되며, 싸이클이 존재하지 않는(tree의 기본 조건) 그래프
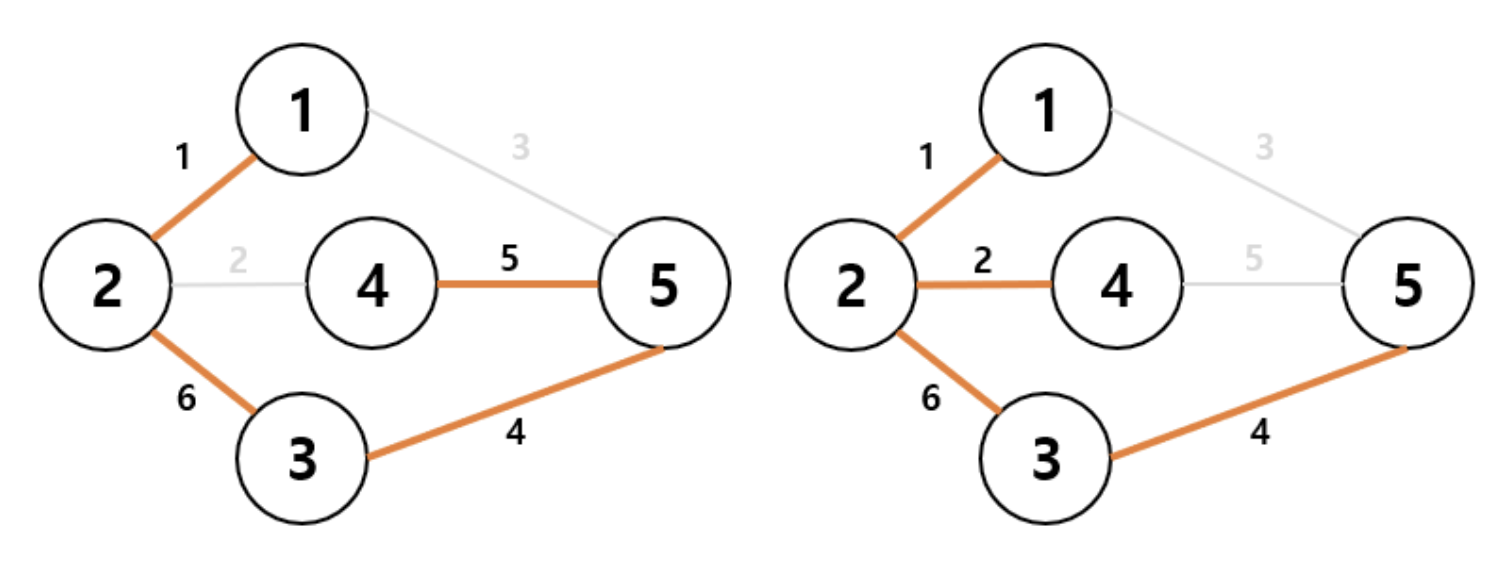
- 위의 그래프에서의 신장 트리 예시
- 신장 트리들 중에서 가중치의 합이 최소가 되는 신장 트리를 최소 신장 트리(Minimum Spanning Tree, MST)라고 한다.
사진 출처 : https://chanhuiseok.github.io/posts/algo-33/
4. 크루스칼 알고리즘의 과정 📝
크루스칼 알고리즘의 과정
- 크루스칼 알고리즘은 그리디 알고리즘의 일종입니다.
- 그래프 간선들을 가중치의 오름차순으로 정렬해 놓은 뒤, 사이클을 형성하지 않는 선에서 정렬된 순서대로 간선을 선택합니다.
1) 그래프 간선들을 가중치의 오름차순으로 정렬한다.
int cmp(vector<int> a, vector<int> b){
return a[2] < b[2];
}
sort(costs.begin(), costs.end(), cmp);2) 사이클을 형성하지 않는 선에서 정렬된 순서대로 간선을 선택한다.
- 정렬된 가중치(비용) 순서대로 사이클을 형성하지 않는다면 해당 비용을 최소 비용에 더해준다!
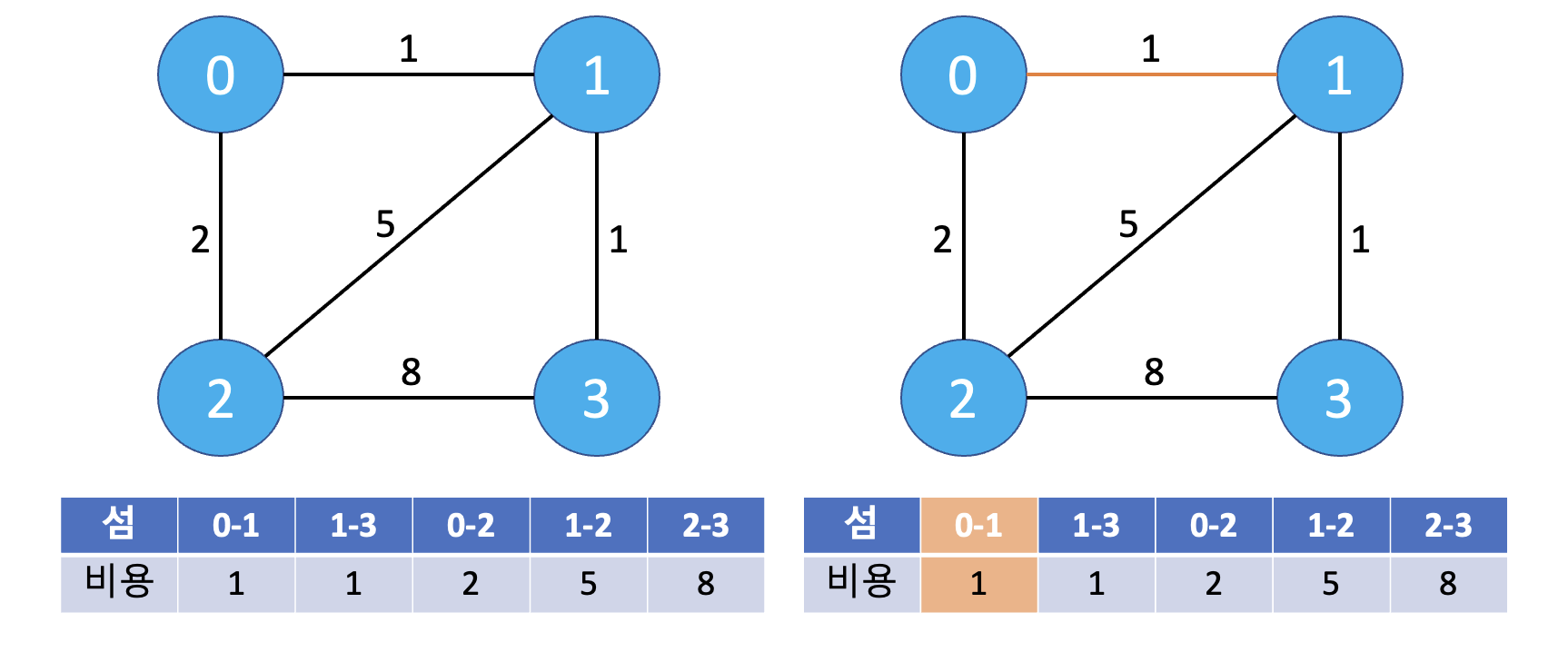
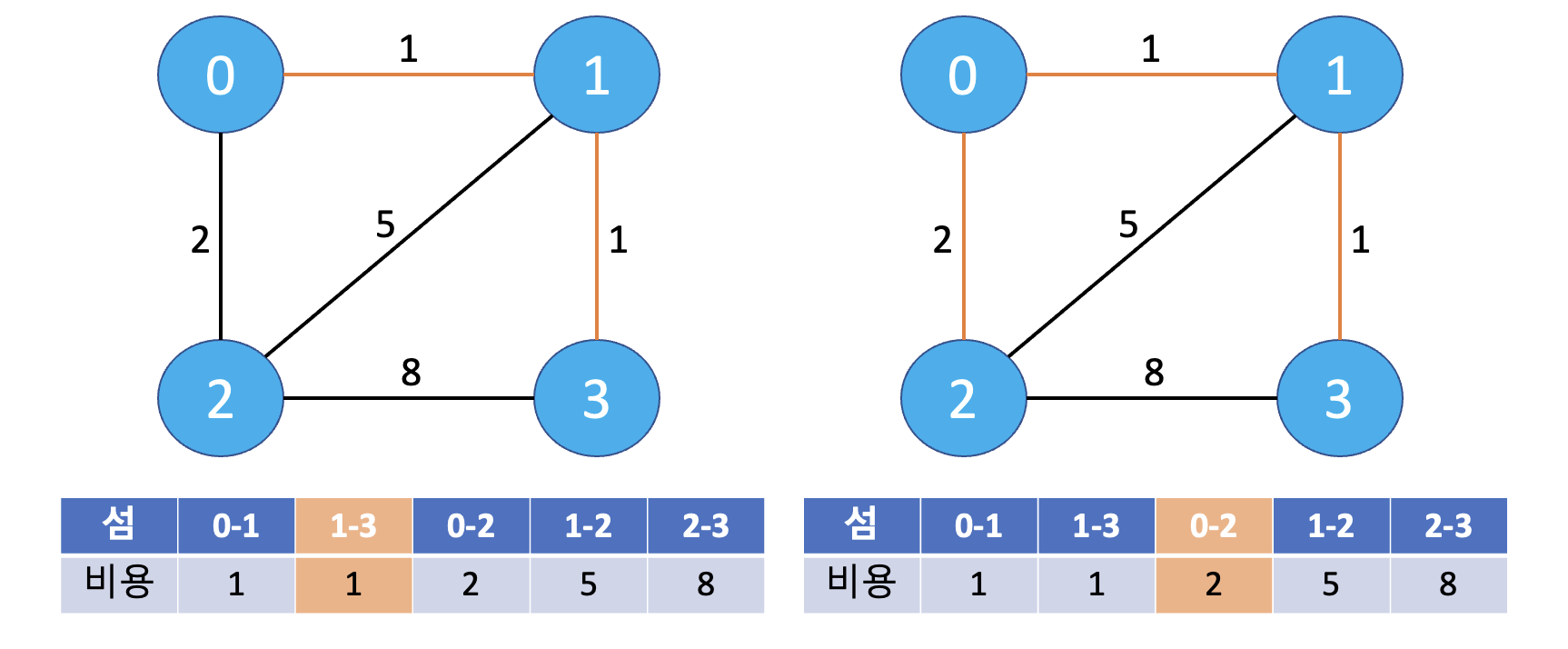
- 이때, 1번과 2번을 연결한 경우, 0번, 1번, 2번 총 3개의 섬이 사이클을 형성하게 된다🔥
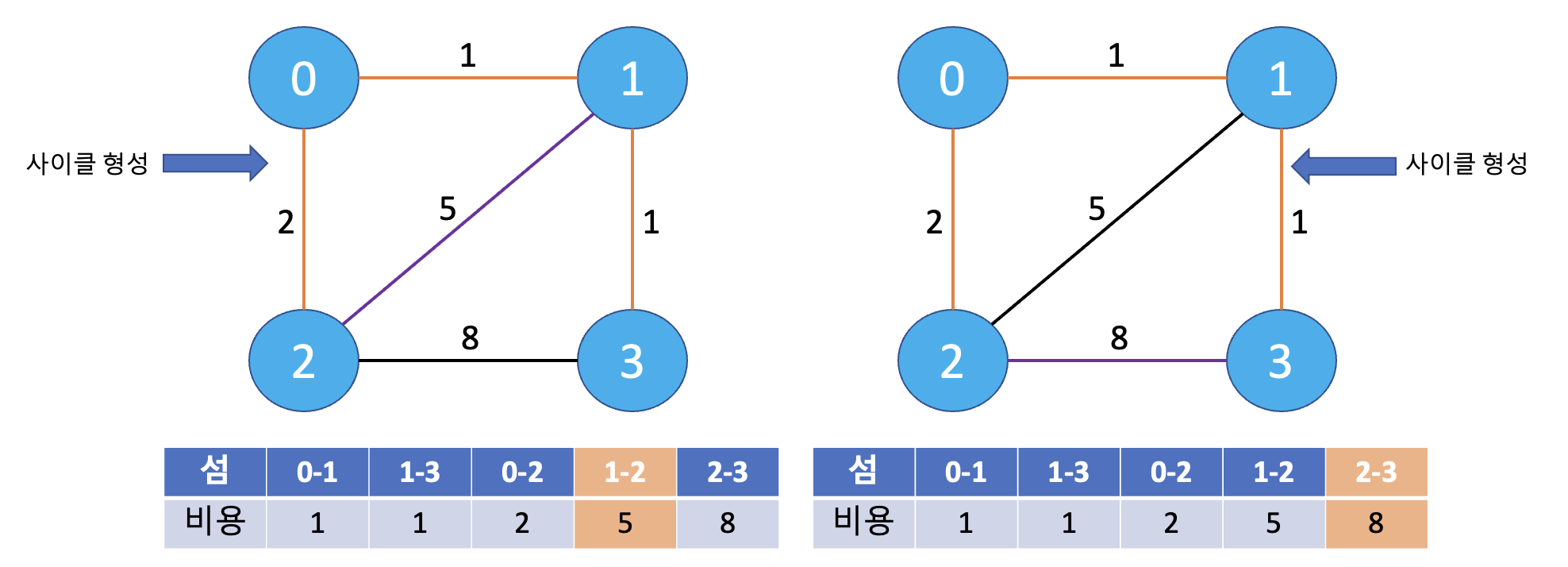
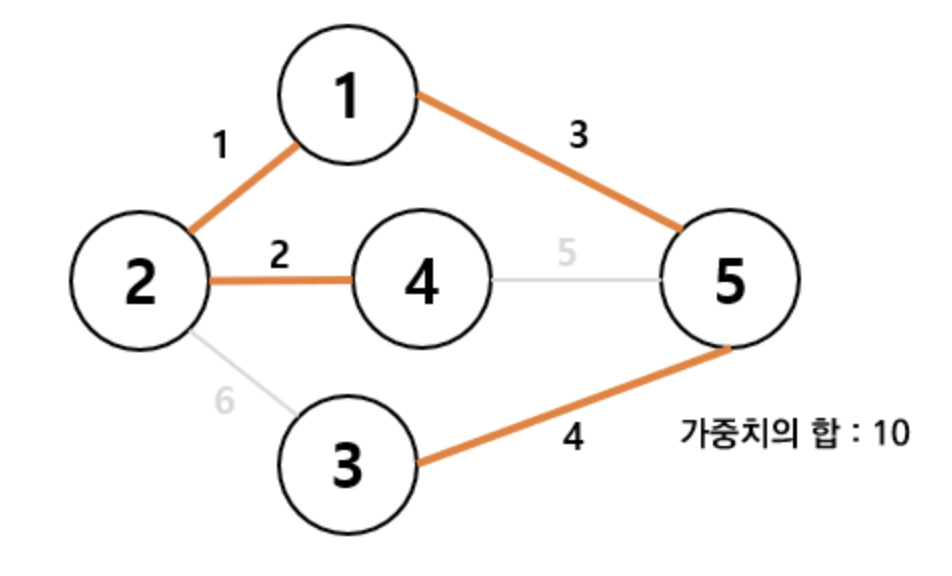
- 아래의 예시는 최종적으로 구한 최소 비용을 가진 신장 트리의 모습이다.
이때 사이클 판단하기 위해서 Union & Find 알고리즘이 활용된다.
☝️ Union-Find 란?
Disjoint Set (서로소 집합) 을 표현하는 자료구조
서로 다른 두 집합을 병합하는 Union 연산, 집합 원소가 어떤 집합에 속해있는지 찾는 Find 연산을 지원하기에 이러한 이름이 붙었다.
- 이때, Union 연산으로 부모 노드를 변경하여, 같은 집합에 속하도록 해준다.
- Find 연산으로 해당 노드의 부모 노드가 다른 노드가 동일한지를 살펴보면서 2개의 노드가 같은 집합에 속한지를 확인해준다.
🔥 같은 집합인 경우, 2개의 노드를 연결해주면 사이클이 형성되어 연결해주지 않는다!!
int find(int x){ //find 연산-> 어떤 집합에 속해있는지 찾는다.
if(parents[x] == x) return x;
return parents[x] = find(parents[x]);
}
...
//union 과정 -> 같은 집합에 있지 않은 경우에만, 두 집합을 병합한다.
int x = find(costs[i][0]);
int y = find(costs[i][1]);
int cost = costs[i][2];
if(x != y){ //사이클을 형성하지 않는다면
parents[y] = x;
answer+=cost;
}5. 전체 코드 🔑
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
int parents[101]; //부모 노드
int cmp(vector<int> a, vector<int> b){
return a[2] < b[2];
}
int find(int x){
if(parents[x] == x) return x;
return parents[x] = find(parents[x]);
}
int solution(int n, vector<vector<int>> costs) {
int answer = 0;
//자기 자신을 부모로 지정
for(int i=0; i<n; i++){
parents[i] = i;
}
sort(costs.begin(), costs.end(), cmp);
for(int i=0; i<costs.size(); i++){
//union 과정
int x = find(costs[i][0]);
int y = find(costs[i][1]);
int cost = costs[i][2];
if(x != y){
parents[y] = x;
answer+=cost;
}
}
return answer;
}6. 결과 🏆