1. 관련 문제 🎯
문제 : 백준 1753 최단 경로 🧭
난이도 : 골드 4
2. 문제 소개 🧩
1️⃣ 방향그래프가 주어지면 주어진 시작점에서 다른 모든 정점으로의 최단 경로를 구한다.
2️⃣ 모든 간선의 가중치는 10 이하의 자연수이다.
3. 문제 풀이 🖌️
해당 문제는 주어진 시작점에서 다른 모든 정점으로의 최단 경로를 구하는 다익스트라의 대표 문제이다.
➡️ 다익스트라 조건인 가중치가 양수여야 한다!!
만약에 문제에서 주어진 조건이 음수가 된다면 다른 알고리즘을 사용해야 한다.
3-1. 유의할 점
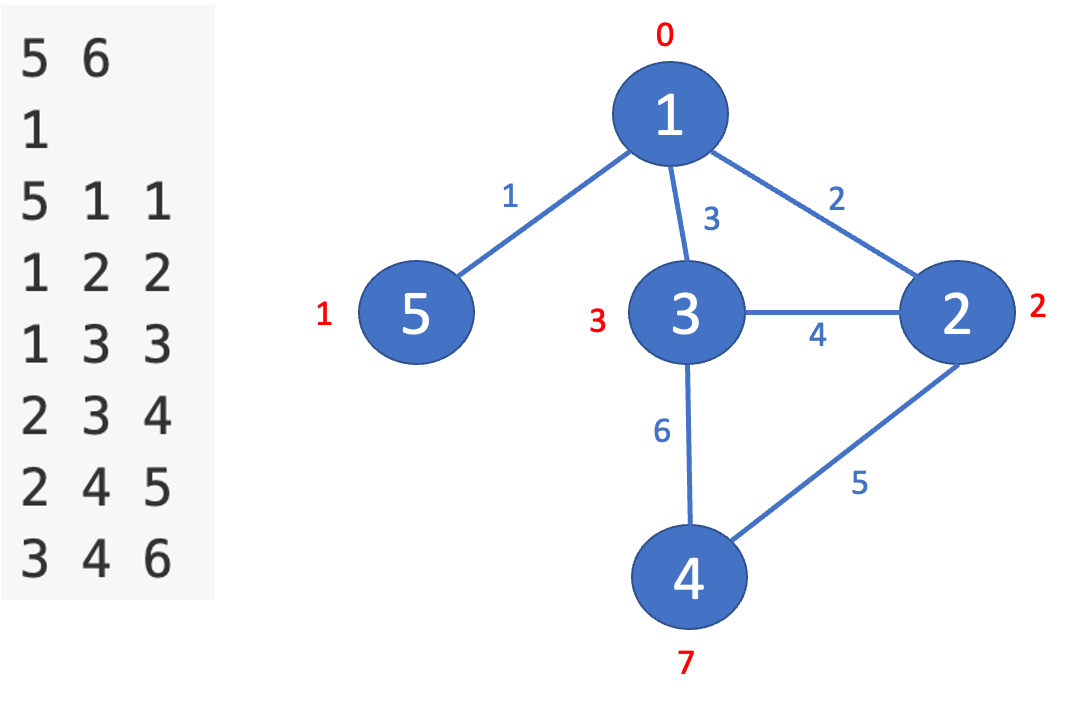
☝️ 이때, 한 가지 생각해야 할 점은 여기에서 만약에 양방향 그래프로 하는 경우 구한 답은 정점 번호를 순서대로 0, 2, 3, 7, 1이 나온다.

🔥 그러나, 주어진 답에서는 1이 아니라 INF가 나온다.
따라서 양방향 그래프가 아니라 단방향 그래프로 그래프를 생성해야 한다!
for(int i=0; i<E; i++){
cin>>u>>v>>w;
graph[u].push_back({v,w});
}3-2. 다익스트라 알고리즘 구현하기
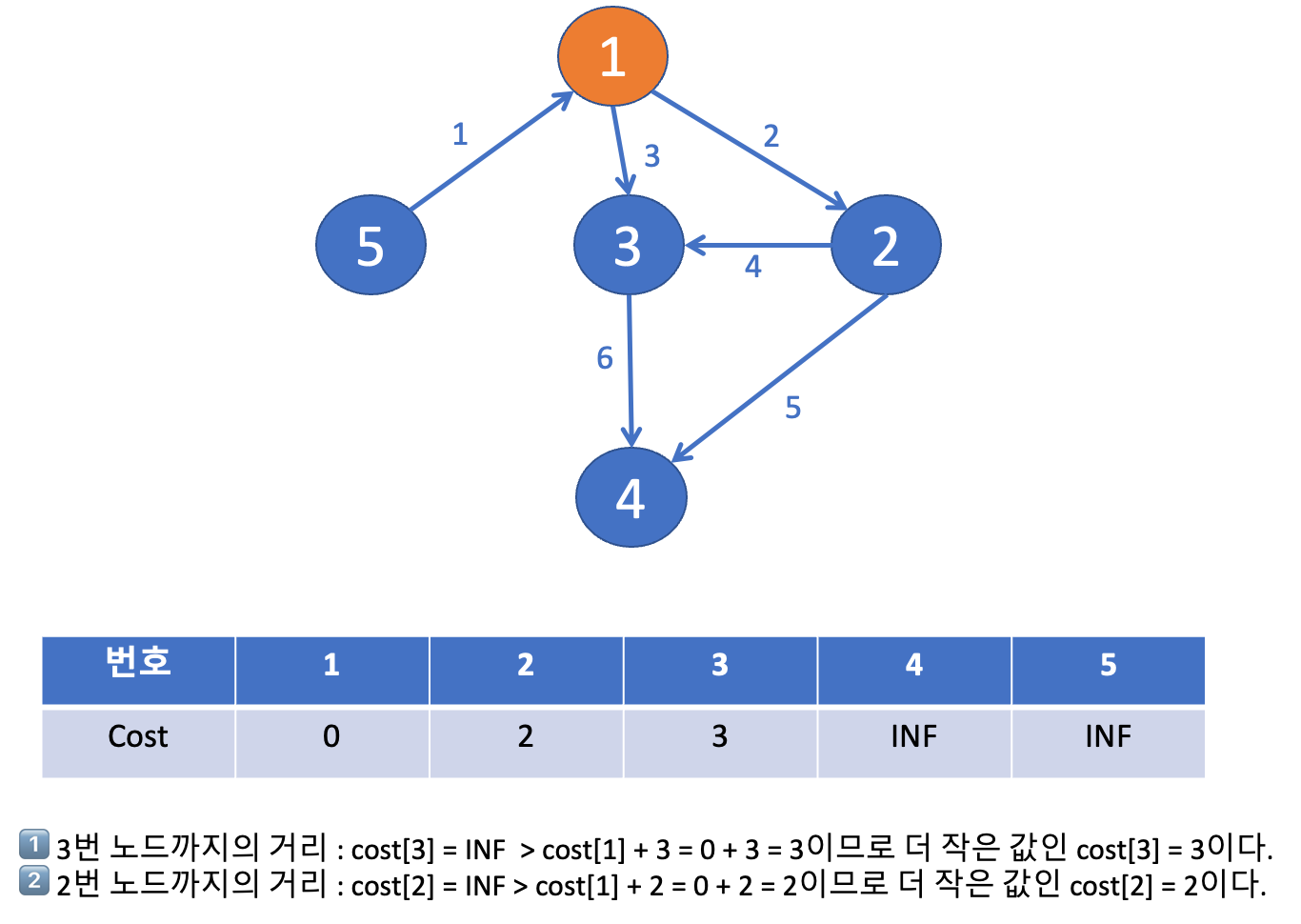
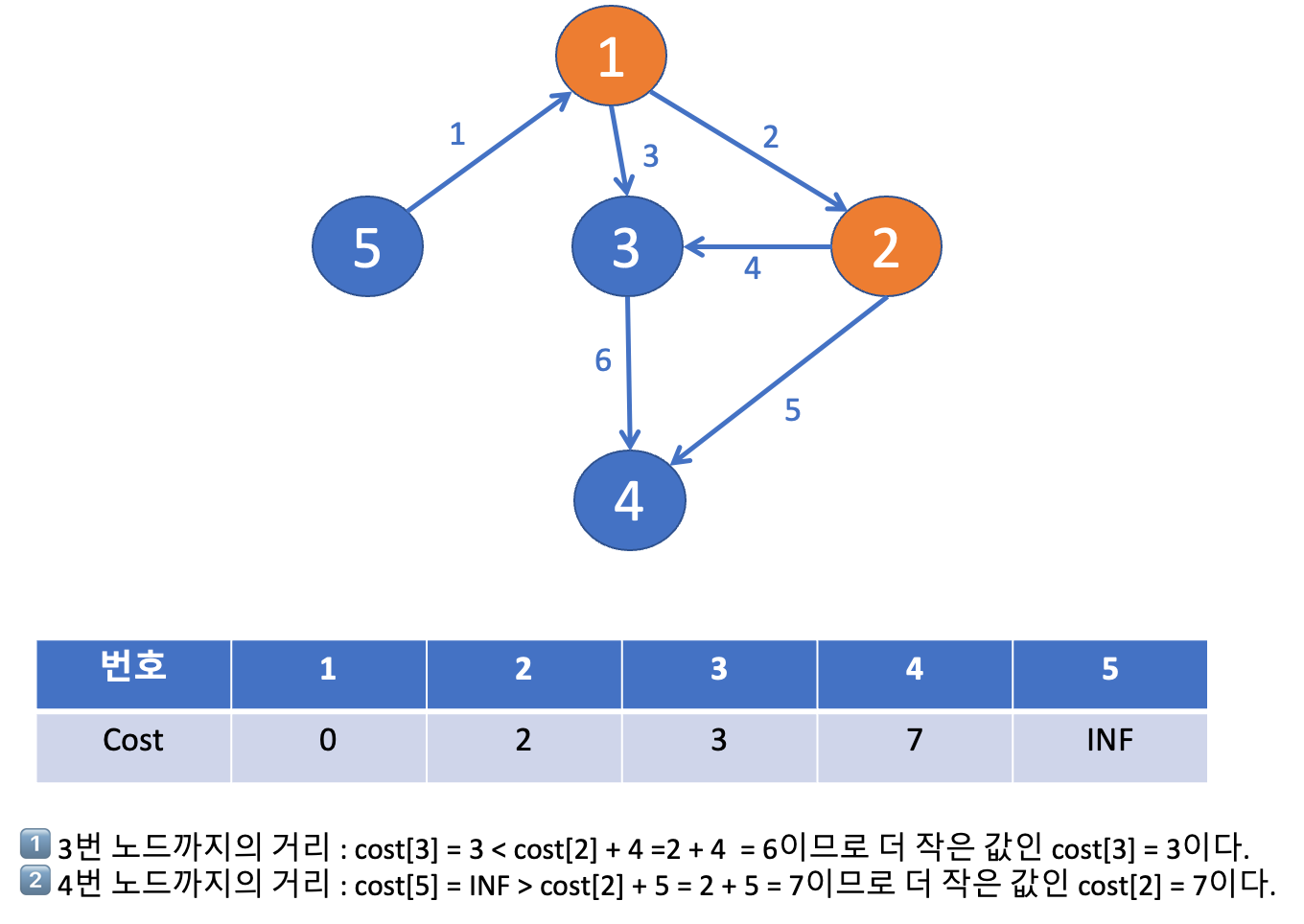
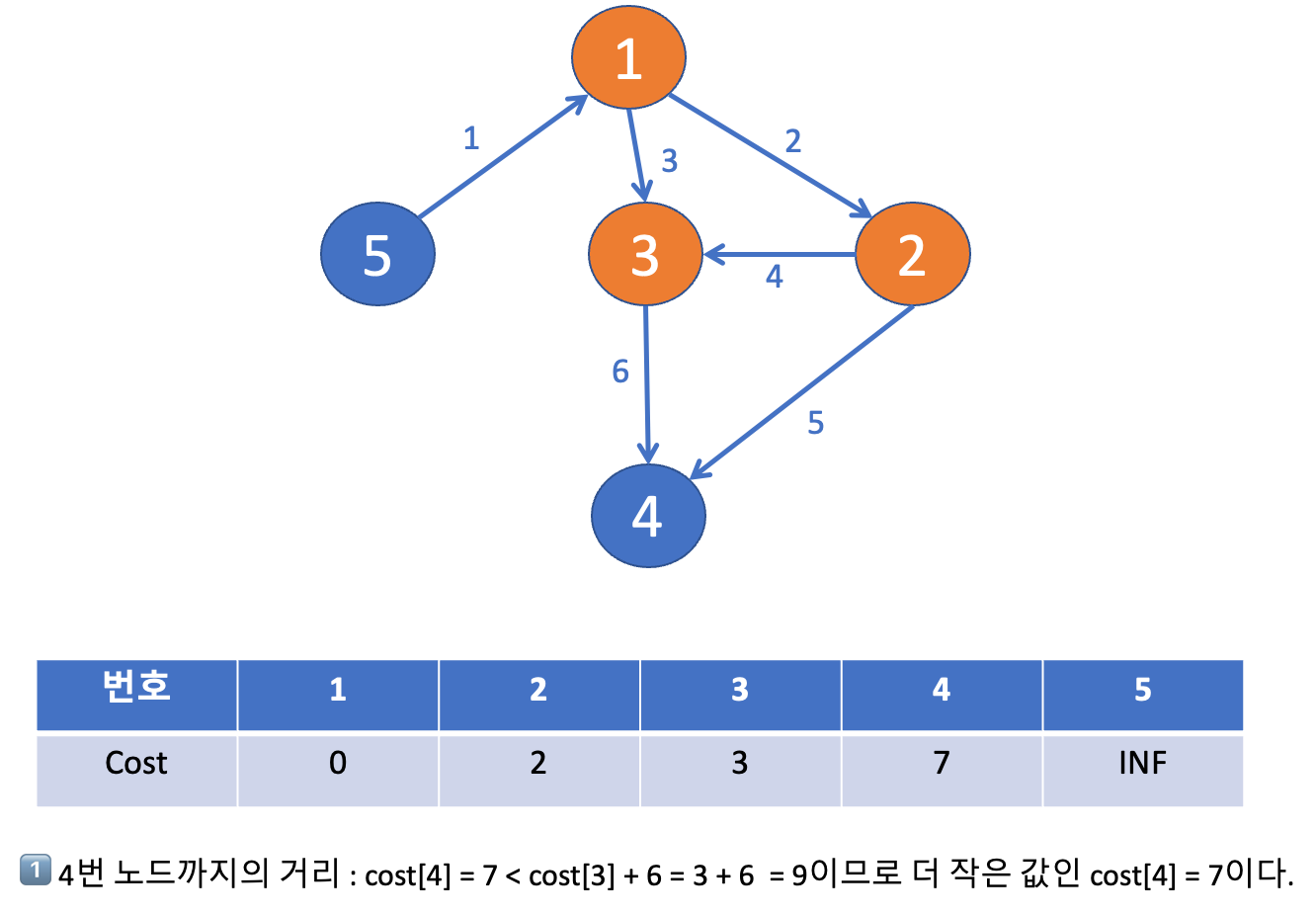
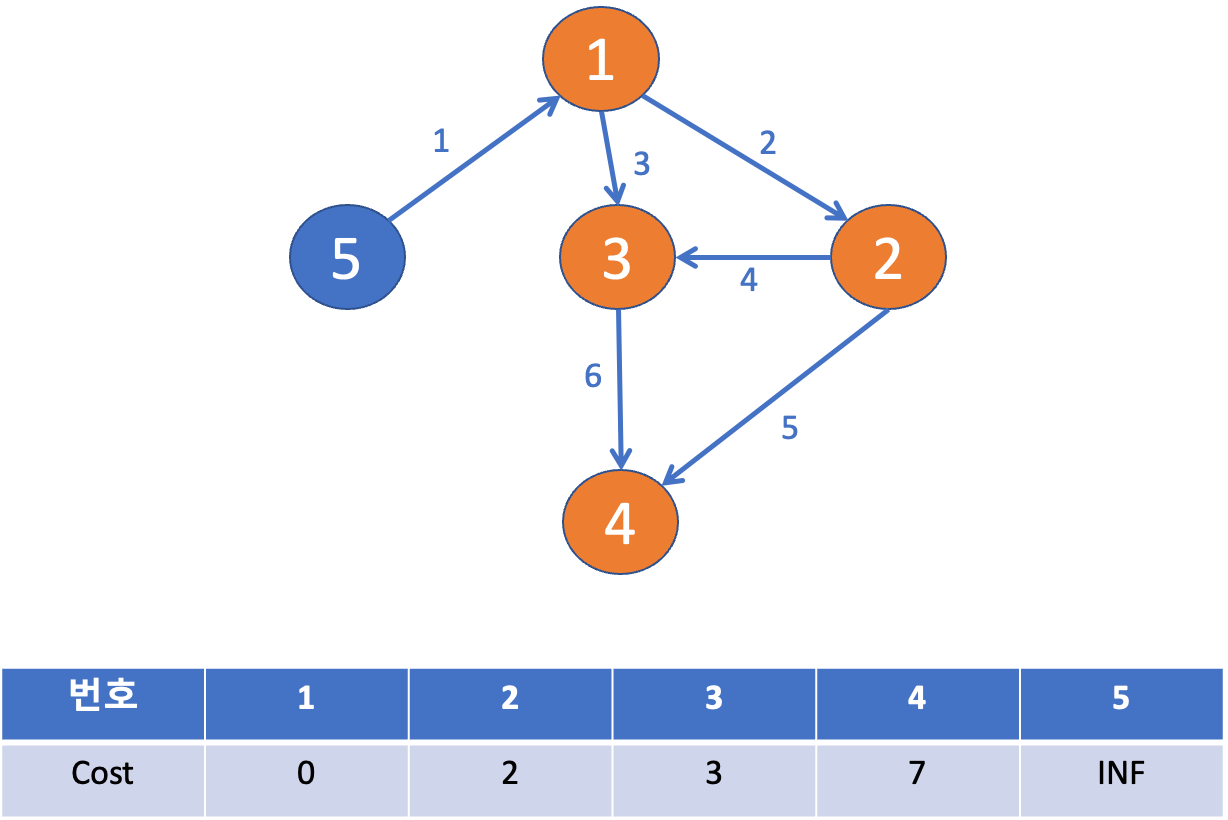
☝️ 주황색 노드는 최단 거리를 구한 노드를 의미하고, 파란색 노드는 최단 거리를 구해야 하는 노드를 의미한다.
✌️ 주황색 노드가 되는 기준은 방문한 노드 중에서 파란색 노드들 중에서 가장 작은 거리를 가진 노드가 된다.
➡️ 가장 작은 거리를 가진 노드를 구하기 위해서, 우선순위 큐 를 사용한다.
+) 우선순위 큐는 pair<int,int>의 경우 첫번째 int를 기준으로 정렬하기 때문에 가장 작은 거리를 구하기 위해서 첫번째에는 거리를 넣어준다.
priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> pq;
...
pq.push({cost[idx], idx});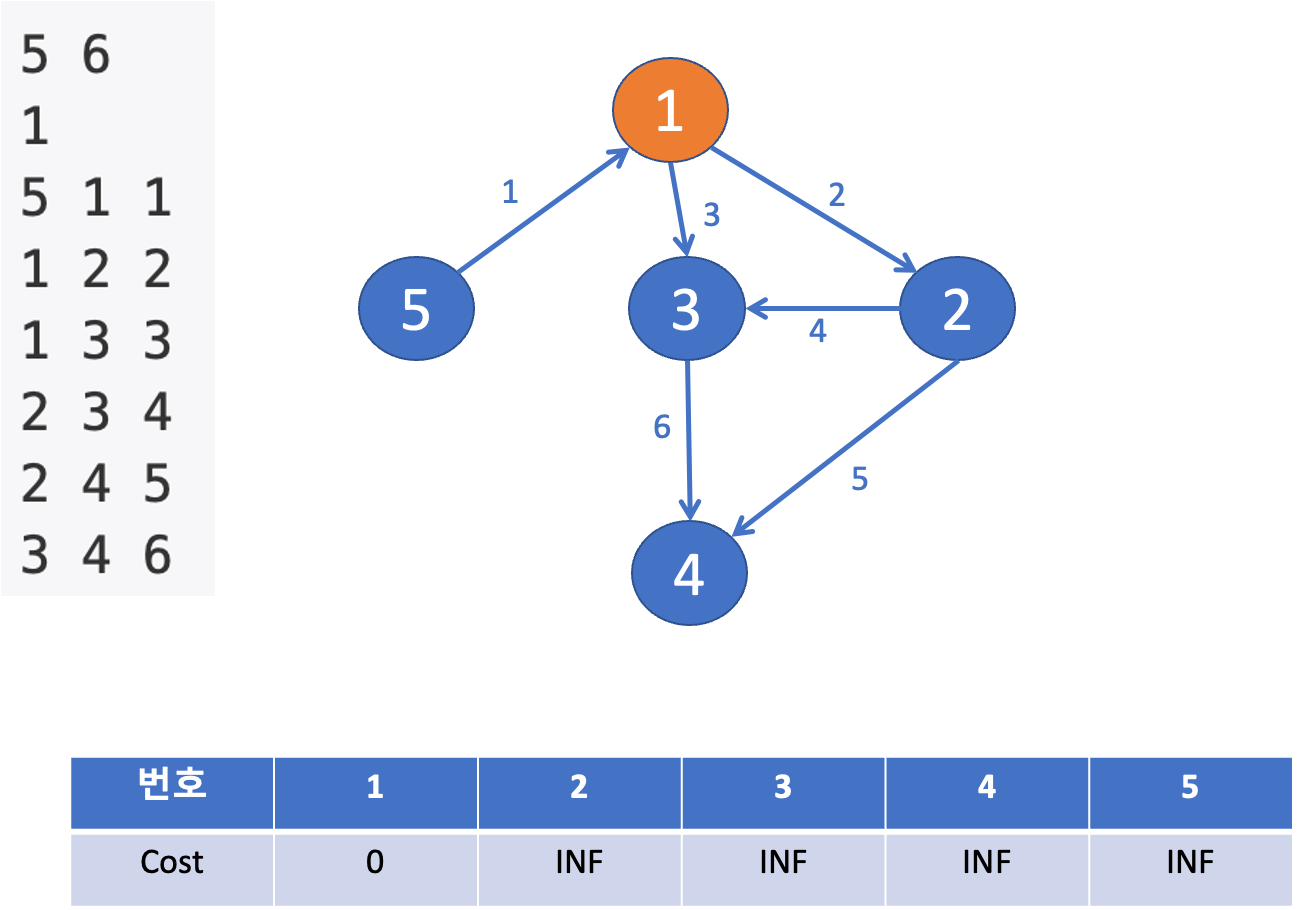
위의 과정을 아래의 전체 코드로 전체적으로 구현할 수 있다!!
4. 전체 코드 🔑
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
#define INF 300001
int main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
int V = 0, E = 0; //정점의 개수, 간선의 개수
int K = 0; //시작 정점
int u = 0, v = 0, w = 0;
cin>>V>>E>>K;
vector<pair<int,int>>graph[V+1]; //연결된 정점의 번호, 가중치
int cost[V+1];
for(int i=0; i<=V; i++){
cost[i] = INF; //cost 무한대로 초기화
}
for(int i=0; i<E; i++){
cin>>u>>v>>w;
graph[u].push_back({v,w});
}
priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> pq;
pq.push({0, K});
cost[K] = 0;
while(!pq.empty()){
int here = pq.top().second;
pq.pop();
for(int i=0; i<graph[here].size(); i++){
int idx = graph[here][i].first;
int weight = graph[here][i].second;
if(cost[idx] > cost[here]+weight){
cost[idx] = cost[here]+weight;
pq.push({cost[idx], idx});
}
}
}
for(int i=1; i<=V; i++){
if(cost[i] == INF){
cout<<"INF"<<"\n";
}
else{
cout<<cost[i]<<"\n";
}
}
}5. 결과 🏆


