3-7. BOJ 1654번 - 랜선 자르기

1. 관련 문제 🎯

문제 : 백준 1654 랜선 자르기 ✂️
난이도 : 실버 2

2. 문제 소개 🧩

1️⃣ 캠프 때 쓸 N개의 랜선을 만들어야 하는데, 자체적으로 K개의 랜선을 가지고 있다.

• 그러나 K개의 랜선은 길이가 제각각이다.

2️⃣ 랜선을 모두 N개의 같은 길이의 랜선으로 만들고 싶었기 때문에, K개의 랜선을 잘라서 만들어야 한다.

• 예를 들어, 300cm 짜리 랜선에서 140cm 짜리 랜선을 두 개 잘라내면 20cm는 버려야 한다. (이미 자른 랜선은 붙일 수 없다.)

3️⃣ 랜선을 자르거나 만들 때 손실되는 길이는 없다.

4️⃣ 기존의 K개의 랜선으로 N개의 랜선을 만들 수 없는 경우는 없다.

5️⃣ 자를 때는 항상 센티미터 단위로 정수 길이만큼 자른다.

6️⃣ N개보다 많이 만드는 것도 N개를 만드는 것에 포함된다.

☝️이때, 만들 수 있는 최대 랜선의 길이를 구해야 한다.

3. 문제 풀이 🖌️

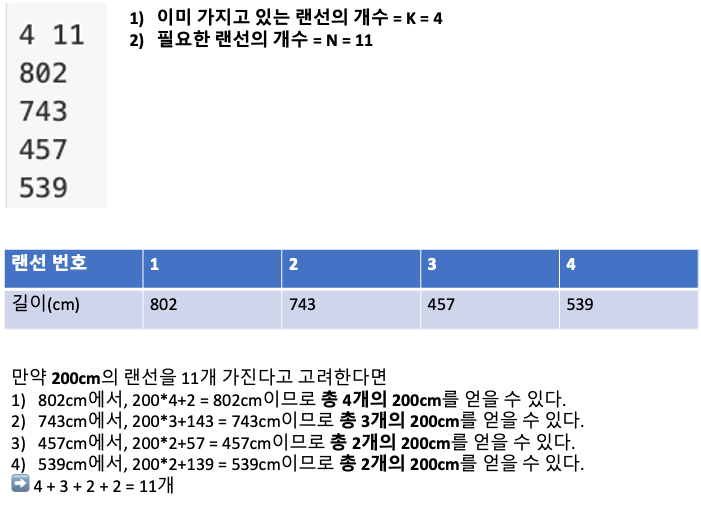
• 먼저 문제를 이해하기 위해서, 최대 랜선의 길이를 200cm로 가정하고 생각해보자!!
  

☝️주목해야 할 점

• 첫 번째로, 구하고자 하는 값은 랜선의 길이라는 점이다!!
• 두 번째로, 구할 수 있는 랜선의 길이의 최솟값은 1cm이고, 최댓값은 주어진 랜선 중에서 최대 길이이다.
• 이때, N은 1이상 1,000,000이하의 정수이므로 N이 1,000,000인 경우, 1~1,000,000에서 최대 랜선의 길이를 구해야 한다.
• 따라서, 1개씩 살펴보면 매우 범위가 넓기 때문에 이분 탐색으로 빠르게 최대 랜선의 길이를 구해야 한다.

✌️ 이분 탐색

• 이분 탐색은 구하고자 하는 값(=최대 랜선의 길이)을 기준으로 찾아야 한다.
• low는 최솟값 1cm이고, high는 주어진 랜선 중에서 최대값이다.

low와 high를 옮기는 기준

1️⃣ mid의 길이로 랜선을 잘랐을 때의 구한 랜선의 개수(cnt_lines) < 구하고자 하는 랜선의 개수(N개)

• 더 작게 잘라야 하므로 high = mid - 1로 변경한다.

2️⃣ mid의 길이로 랜선을 잘랐을 때의 구한 랜선의 개수(cnt_lines) > 구하고자 하는 랜선의 개수(N개)

• 더 크게 잘라야 하므로 low = mid + 1로 변경한다.

✨ 이때, 중요한 점은 mid의 길이로 랜선을 잘랐을 때의 구한 랜선의 개수(cnt_lines)와 구하고자 하는 랜선의 개수가 동일한 경우이다.

• 여기에서는 최대 랜선의 길이를 구해야 하므로 만약 300cm로 자르고 350cm로 잘랐을 때 총 11개로 잘라진 랜선의 개수가 동일해도 350cm를 선택해야 한다.
• 따라서, 더 크게 자르기 위해서 동일한 경우에도 low = mid + 1로 변경한다.

따라서, ans = 200이므로 해당 문제의 답은 200이 된다.

4. 전체 코드 🔑

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

vector<int> lines;

//mid의 길이로 랜선을 잘랐을 때의 랜선의 개수 구하기
int cut_lines(int length){
    int cnt = 0;
    for(int i=0; i<lines.size(); i++){
        cnt += lines[i]/length;
    }
    return cnt;
}

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL); cout.tie(NULL);

    int K = 0, N = 0;
    int line_length = 0;
    int max_line = 0;

    cin>>K>>N;
    
    for(int i=0; i<K; i++){
        cin>>line_length;
        lines.push_back(line_length);
        max_line = max(max_line, line_length);
    }

    long long low = 1;
    long long high = max_line;
    long long ans = 0;

    while(low <= high){
        long long mid = (low + high) / 2;
        int cnt_lines = cut_lines(mid);

        if(cnt_lines < N){
            high = mid - 1;
        }
        else{
            low = mid + 1;
            ans = mid;
        }
    }

    cout<<ans<<"\n";

    return 0;
}

5. 결과 🏆