참고 자료 : https://hongchan.tistory.com/5
위의 블로그를 참고하여, 정리하였으며 추가적으로 정리할 부분도 추가하였습니다.
1. 순열(Permutation)
- 순서를 따지고, 중복을 허용하지 않는다. (순서O, 중복X)
- 중복을 검사하기 위한 check 배열을 사용한다.
- depth를 하나씩 늘려가며, 배열에 하나씩 채우는 방법으로 재귀를 수행한다.
#include <iostream>
#include <vector>
using namespace std;
int n = 3, r = 2;
int arr[3] = {1,2,3}; //arr[n]
vector<int> v;
bool check[4] = {false, }; //check[n] -> 중복 제거
void permutation(int cnt){
//nPr : n개 중에 r개를 뽑아 나열할 수 있는 경우의 수(중복 허용x)
if(cnt == r){
for(int i : v){
cout<<i<<" ";
}
cout<<"\n";
return;
}
for(int i=0; i<n; i++){
if(!check[arr[i]]){
v.push_back(arr[i]);
check[arr[i]] = true;
permutation(cnt+1);
check[arr[i]] = false;
v.pop_back();
}
}
}
int main(){
permutation(0);
}결과
1 2
1 3
2 1
2 3
3 1
3 2
1-1. 관련 문제 1 : N과 M (1)
https://www.acmicpc.net/problem/15649
- 1부터 N까지 자연수 중에서 중복 없이 M개를 고른 수열을 구한다.
2. 중복 순열
- 순서를 따지고, 중복을 허용한다. (순서O, 중복O)
- 중복 검사를 제외하면 위의 순열 코드와 동일하다.
#include <iostream>
#include <vector>
using namespace std;
int n = 3, r = 2;
int arr[3] = {1,2,3}; //arr[n]
vector<int> v;
void permutation(int cnt){ //중복순열
if(cnt == r){
for(int i : v){
cout<<i<<" ";
}
cout<<"\n";
return;
}
for(int i=0; i<n; i++){
v.push_back(arr[i]);
permutation(cnt+1);
v.pop_back();
}
}
int main(){
permutation(0);
}결과
1 1
1 2
1 3
2 1
2 2
2 3
3 1
3 2
2-1. 관련 문제 : N과 M (3)
https://www.acmicpc.net/problem/15651
- 1부터 N까지 자연수 중에서 M개를 고른 수열이고, 같은 수를 여러 번 골라도 된다.
2-2. 관련 문제 2 : 1, 2, 3 더하기
https://www.acmicpc.net/problem/9095
3. 조합 (Combination)
- 순서를 따지지 않고, 중복을 허용하지 않는다. (순서X, 중복X)
- 반복문을 돌며, 모든 경우에 대해 선택하는 것은 위의 경우들과 같다.
- 그러나, 반복문의 시작 값은 이전에 선택한 값 + 1이 된다.
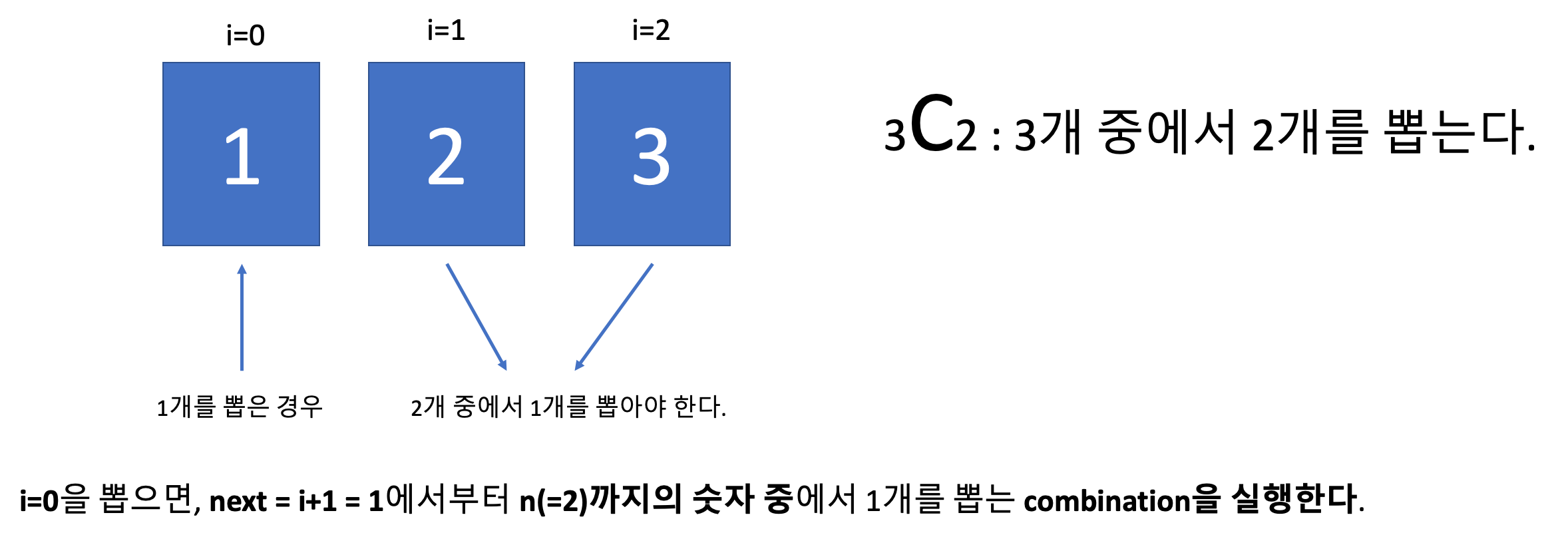
- 위의 사진을 통해서, 반복문의 시작 값은 이전에 선택한 값+1(next = i+1)이 되는 이유를 알아낼 수 있다!!
#include <iostream>
#include <vector>
using namespace std;
int n = 3, r = 2;
int arr[3] = {1,2,3}; //arr[n]
vector<int> v;
void combination(int cnt, int next){ //조합
if(cnt == r){
for(int i : v){
cout<<i<<" ";
}
cout<<"\n";
return;
}
for(int i=next; i<n; i++){
v.push_back(arr[i]);
combination(cnt+1, i+1);
v.pop_back();
}
}
int main(){
combination(0,0);
}결과
1 2
1 3
2 3
3-1. 관련 문제 : N과 M(2)
https://www.acmicpc.net/problem/15650
- 1부터 N까지 자연수 중에서 중복 없이 M개를 고른 수열이고,
고른 수열은 오름차순이어야 한다.
4. 중복 조합
- 순서를 따지지 않고, 중복을 허용한다. (순서X, 중복O)
- 조합과 구현이 비슷하지만, 반복문의 시작 값은 이전에 선택한 값이 된다.
#include <iostream>
#include <vector>
using namespace std;
int n = 3, r = 2;
int arr[3] = {1,2,3}; //arr[n]
vector<int> v;
void combination(int cnt, int next){ //조합
if(cnt == r){
for(int i : v){
cout<<i<<" ";
}
cout<<"\n";
return;
}
for(int i=next; i<n; i++){
v.push_back(arr[i]);
combination(cnt+1, i);
v.pop_back();
}
}
int main(){
combination(0,0);
}결과
1 1
1 2
1 3
2 2
2 3
3 3
4-1. 관련 문제 : N과 M (4)
https://www.acmicpc.net/problem/15652
- 1부터 N까지 자연수 중에서 M개를 고른 수열
- 같은 수를 여러 번 골라도 된다.
- 고른 수열은 비내림차순이어야 한다.
- 길이가 K인 수열 A가 A1 ≤ A2 ≤ ... ≤ AK-1 ≤ AK를 만족하면, 비내림차순이라고 한다.

