이 글은 어떤 과정을 통해 해당 문제를 풀고 이해할 수 있었는지를 정리하기 위해 작성하였습니다!
문제 링크
https://www.acmicpc.net/problem/15486
문제
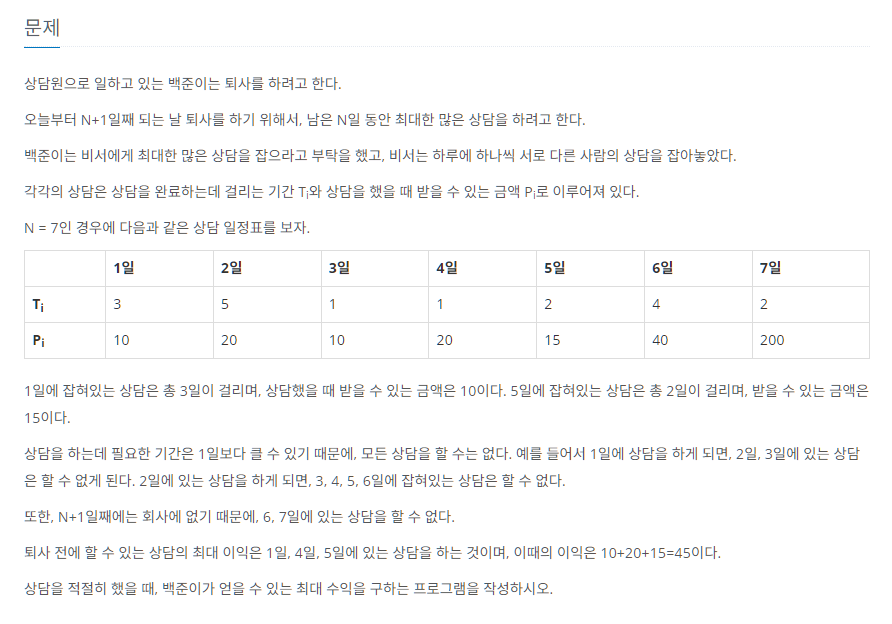
- 해당 문제는 dp를 통해서 풀어야 한다.
=> 완전 탐색으로 풀 경우 (1 ≤ N ≤ 1,500,000) 시간초과가 날 것임 - N+1날 퇴사를 하기 때문에, N일까지 최대한의 금액을 벌어 일을 끝내야만 한다.
🚨 단, N+1일 전에 일을 시작했어도 마무리가 N+1이후까지 진행되는 것이면, 수익으로 인정하지 X
💬 출력값 : 퇴사 일 전까지 최대한 수익을 벌었을 경우의 최댓값
2. 접근 방식
N+1일에 퇴사를 함 -> N일까지 일을 마무리 지어야 함
예시가 이렇게 된다고 했을 때, 7일에 끝을 내야 한단 것이다.
7
3 10
5 20
1 10
1 20
2 15
4 40
2 200
7일차의 상담은 7+2 = 9로 7을 초과 (x)
6일차의 상담은 6+4 = 10으로 초과 (x)
5일차의 상담은 5+2 = 7로 초과하지 않음 (⭕)
그렇게 되면 dp[5]에는 우리는 최댓값을 구해야 되기 때문에, 가장 큰 최댓값이 들어가야 한다.
p[5] + 5일까지 벌어들인 dp값, 혹은 지금까지의 값 중 최댓값 이들 중 더 큰 값이 기록되게 된다.
dp[i] = max(p[i] + dp[t[i] + i], max값)
5일차에 dp[5] = p[5] + dp[7]이 되는데, dp[7]은 아직 갱신된 적이 없어 값이 0이 된다.
=> dp[5] = 15
다음으로 최댓값을 갱신하여 max_value = dp[5] = 15가 된다.
4일차도 1일이 걸리므로 진행가능하다.
dp[4] = p[4] + dp[t[4] + 4] = p[4] + dp[5] = 20 + 15=35이다.
- max_value는 15에서 -> 35으로 갱신
3일차도 1일이 걸리므로 진행됨.
dp[3] = p[3] + dp[t[3] + 3] = p[3] + dp[4] = 10 + 35 = 45
- max_value는 갱신 45
2일차는 5일이 진행된다. 가능하다. 2+5 = 7일차니까!
dp[2] = p[2] + dp[t[2] + 2] = p[2] + dp[7] = 20 + 0 = 20
- max_value = 45 이다. 20은 45보다 작기 때문에 갱신될 수 없고,
이로인해 dp[2] = 45로, 최댓값으로 유지한다.
1일차는 4일이 진행된다. 가능하다 -> 1+4 = 5일차니까
dp[1] = p[1] + dp[t[1] + 1] = p[1] + dp[4] = 10 + 35 = 45
- max_value = 45 로 유지되며 이 값을 출력해내면 된다.
여기서 잠깐
p[i] + dp[t[i] + i] 에서 dp[t[i] + i]는 뒤의 자리를 가리키는게 아닌가? 🤔🤔
라고 생각할 수 있는 이들에게
우리는 역순으로 계산을 하고 있기 때문에 여기서의 기준으로 이전 값이란 우리의 뒤에 값들이란 것을 잊지말자!
2-1. 시간초과가 난 코드 (_해결함)
제출했을 때는 N의 값을 신경쓰지 않아서 '퇴사'와 같이 풀었더니 시간초과가 떴다.😢
'''
[DP] 퇴사2 (골 5)
조건 : n일까지만 근무
goal: 백준이가 얻을 수 있는 최대 수익을 구하라
'''
import sys
input = sys.stdin.readline
n = int(input())
t = []
p = []
dp = [0] * (n + 1)
for _ in range(n):
ti, pi = map(int, input().rstrip().split())
t.append(ti)
p.append(pi)
#idx + t = 가능한 날의 idx
#idx 날 근무를 할지, pass 할지
'''
최대이익
t가 지나가
'''
for idx in range(n-1,-1,-1):
#퇴사날을 넘긴다(진행할 수 x)
if idx + t[idx] > n:
dp[idx] = dp[idx + 1] #(최댓값,0)을 그대로 저장
else:
#다른경우를 방문한 dp vs 그 직전 방문한 dp를 비교 후 -> 최댓값을 삽입
# 목표는 최댓값을 가지도록 해야함
dp[idx] = max(p[idx] + dp[t[idx]+idx], dp[idx+1])
#최종적으로 최댓값을 출력할 수 밖에 없음
print(dp[0])내 코드에서의 문제점은 이런게 있었다.
- N의 조건을 생각하지 않음
- 역순으로 풀다보니 불필요한 반복이 있을 수 있다.
-> 특정 조건에서 종료를 해도 좋을 것임.
결과적으로 대량의 데이터를 최적화하기 위해 '입력시간을 줄였다'
sys.stdin.readline을 이용하여 해결했다.

그러나 시간이 꽤나 걸린 것을 알 수 있었다..
좀 더 시간이 덜 걸리고 다른 방식으로 푸신 분들이 궁금했다.
✨2-1. 다른 코드
그래도 다른 방법을 더 확인하고 싶어 다른 분들의 코드를 참고했다.
import sys
input = sys.stdin.readline
n = int(input())
t, p = [0 for _ in range(n + 1)], [0 for _ in range(n + 1)]
for i in range(1, n + 1):
t[i], p[i] = map(int, input().split())
dp = [0 for _ in range(n + 1)]
for i in range(1, n + 1):
dp[i] = max(dp[i], dp[i - 1]) # 이전까지의 최댓값
fin_date = i + t[i] - 1 # 당일 포함
print("i값", i, "findate = ", fin_date)
if fin_date <= n: # 최종일 안에 일이 끝나는 경우
# i일부터는 일을 해야하므로 i일에 얻을 수 있는 최댓값이 아닌 i-1일까지 얻을 수 있는 최댓값을 구한다
dp[fin_date] = max(dp[fin_date], dp[i - 1] + p[i])
print(max(dp))시간 복잡도가 비슷하단 것을 알 수 있었다. 이를 줄이기 위해서는 계산 부분에서 불필요한 계산을 줄일 수 있도록 수정하는 것이 가장 best인 것 같다.
