
그리디 알고리즘은 최적해를 구하는 데에 사용되는 알고리즘 중 하나이다.
여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달한다.
순간마다 최고의 선택을 한다고 해서 그 선택들이 모여 만들어진 해답이 그것이 최적이라는 보장은 없다.
하지만 그리디 알고리즘을 적용할 수 있는 문제들은 매 순간 최선의 선택을 한다면 최적의 결과를 보장한다.
한 줄 요약 (두 줄인가)

이 문제를 풀면 당신도 멀티탭을 개이득보면서 사용 할 수 있을 것이다.
내가 코드를 꽂는다고 할 때 경우의 수를 생각해보자,
- 멀티탭 자리가 있을 때
: 개이득 그냥 꽂으면 된다. - 멀티탭 자리가 없을 때
: 이후에 다시 안 쓸 코드을 뽑아서 거기다 꽂으면 된다. 여기까진 뭐 쉽다.
:: 이후에 멀티탭을 다시쓴다면?
2-2번의 경우가 문제가 된다.
최대한 덜 뽑기 위해서는 어떻게 해야할까?
논리적으로 생각해보자. 다시 사용할 일이 최대한 늦게 나는 코드를 뽑는게 좋을까? 아니면 빨리 나는 코드를 뽑는게 좋을까?
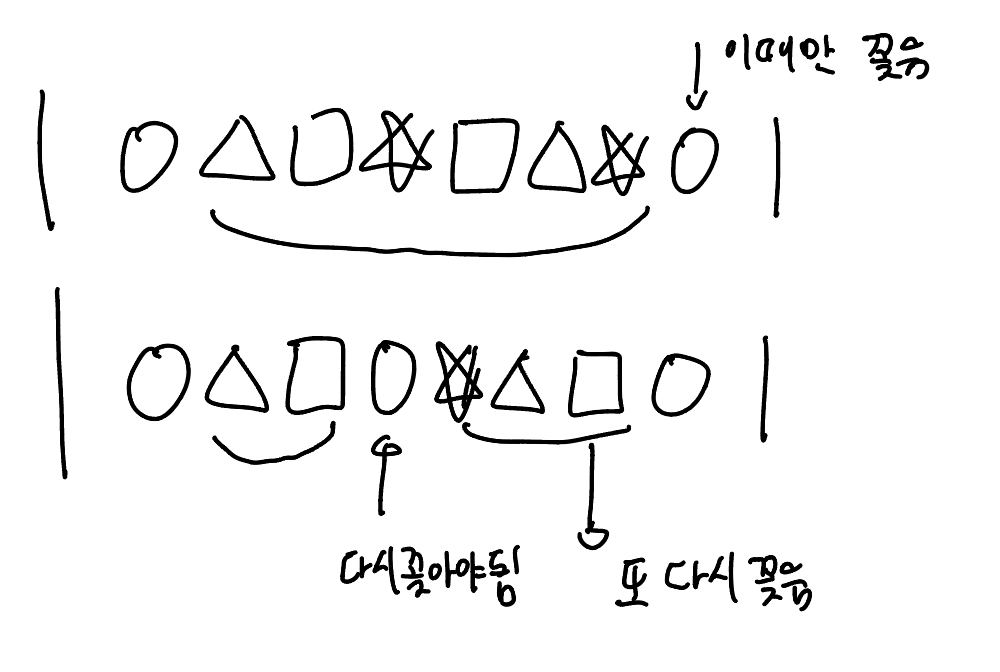
사진을 보면 똑같이 한 번만 o모양 코드를 뽑았다 꽂았지만, 나중에 꽂을 경우 코드를 뽑는 횟수가 더 줄어든다는 것을 알 수 있다.
그러면 2-2번의 경우 앞으로 사용할 목록 중에 가장 늦게 사용할 코드를 뽑으면 코드를 꽂았다 뽑을 일을 최소화 할 수 있을 것이다.
이러한 조건을 확인해 볼 때, 우리는 매 순간 이러한 조건을 모두 만족시키는 최선의 선택만을 해나간다면, 최적의 답을 구할 수 있음을 알 수 있다.
import sys
from collections import deque
input = sys.stdin.readline
n, k = map(int, input().split())
items = deque(map(int, input().split()))
tap = [0] * n
ans = 0
while items:
if items[0] in tap:
items.popleft()
elif 0 in tap:
# 콘센트의 자리가 있다면.
tap[tap.index(0)] = items.popleft()
# 콘센트에 꽂는다.
# 콘센트에 꽂았으니까 꽂을 리스트에서 제외한다.
# 콘센트에 자리가 없다면.
else:
tap_index = []
for i in tap:
if i not in items:
# 앞으로 뽑을 리스트에 없는 콘센트를 찾는다
tap_index.append(sys.maxsize)
break
else:
# 꽂혀있는 아이템들이 나중에 쓰일거라면
# 꽂혀있는 아이템의 index를 비교를 어떻게 하지
tap_index.append(items.index(i))
# 인덱스 모아놓은 곳에서 가장 큰 인덱스를 가진 멀티탭을 뽑는다.
tap[tap_index.index(max(tap_index))] = items.popleft()
ans += 1
print(ans)
