이진트리(Binary Tree)는 다음과 같이 root와 edge로 연결된 노드를 의미한다.
이진 트리는 데이터 저장 목적으로 사용되는 자료 구조로. 각 노드가 최대 두 개의 자식을 가질 수 있는 조건을 가지고 있다. 이진 트리는 정렬된 배열과 연결 리스트처럼 검색이 빠르고 삽입 또는 삭제 작업이 연결 리스트에서처럼 빠르기 때문에 해당 이점을 모두 갖고 있다.
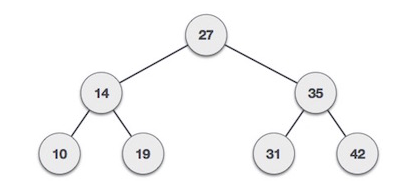
bifurcating arborescence라고도 불리는데 한국어로는 두 갈래로 갈라진 나뭇가지라는 의미를 가진다.
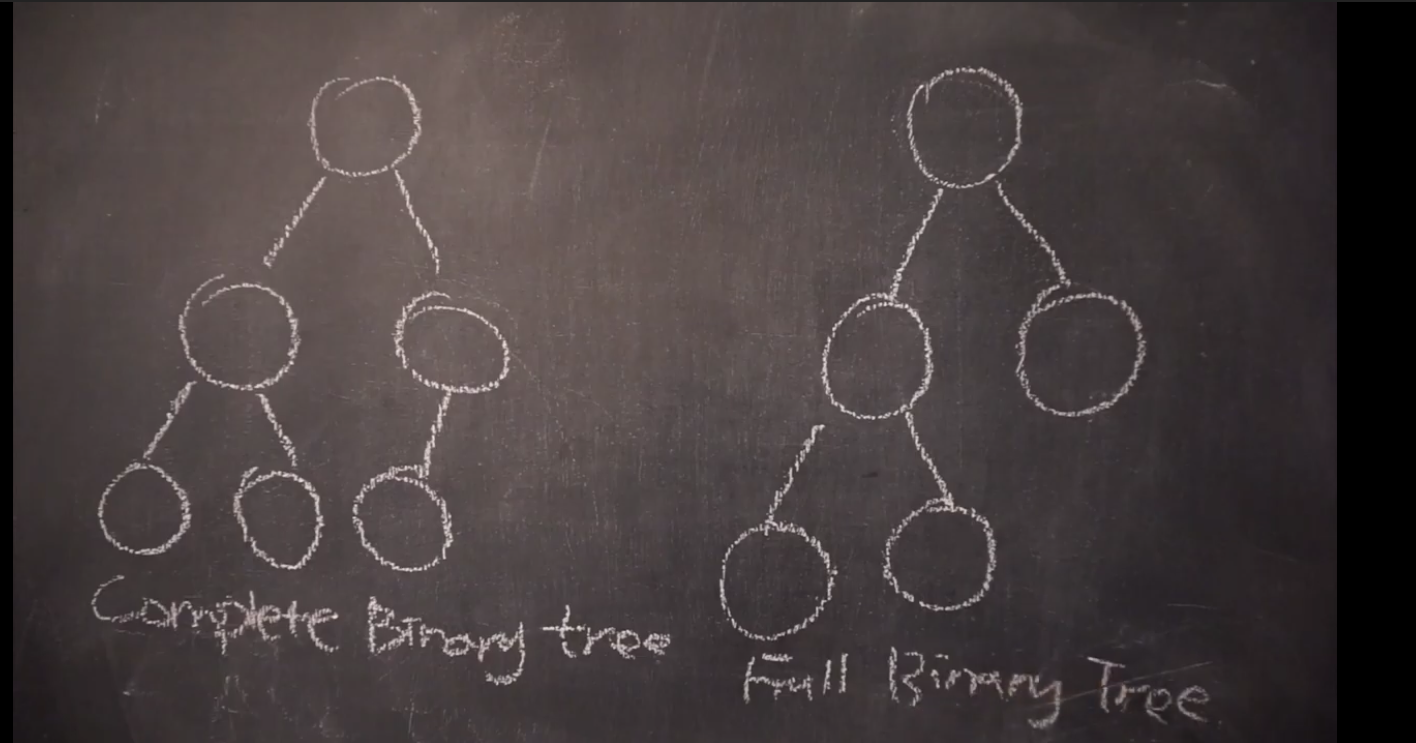
자식 노드(child-nord)의 구성에 따라 이진트리의 분류도 나뉜다.
자식노드가 왼쪽부터 위치하면 Complete Binary Tree,
자식노드가 2개 모두 있거나 혹은 아예 없는 경우 Full Binary Tree로 분류한다.
트리의 순회

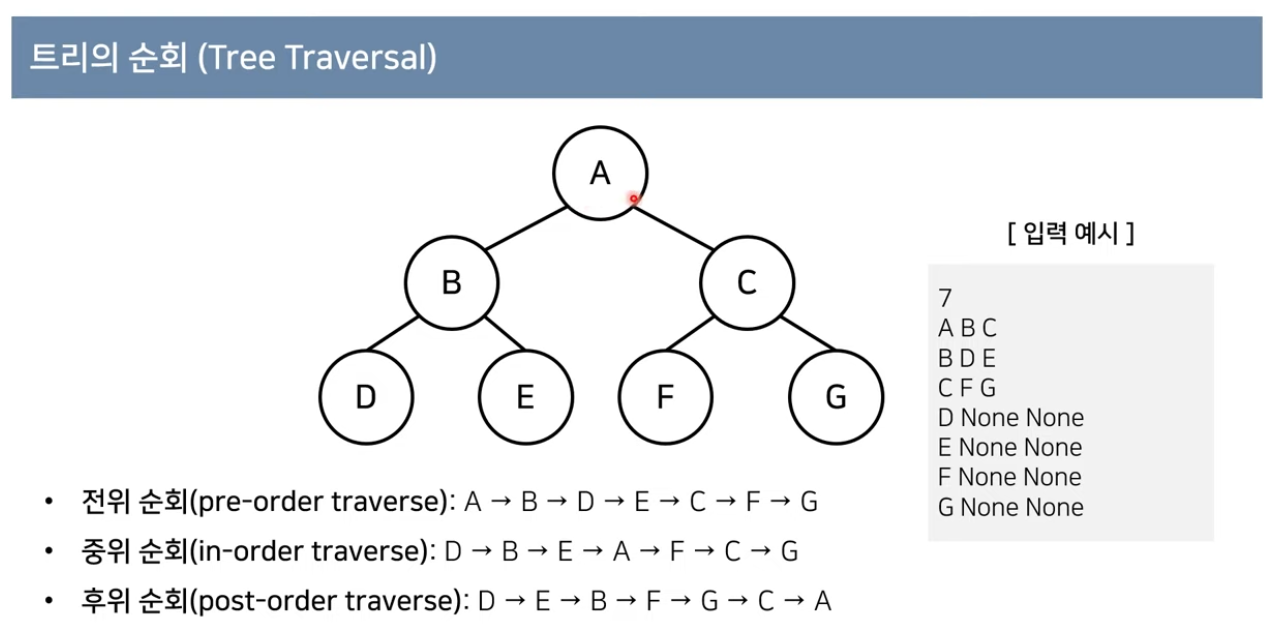
예시 - 백준 1991번

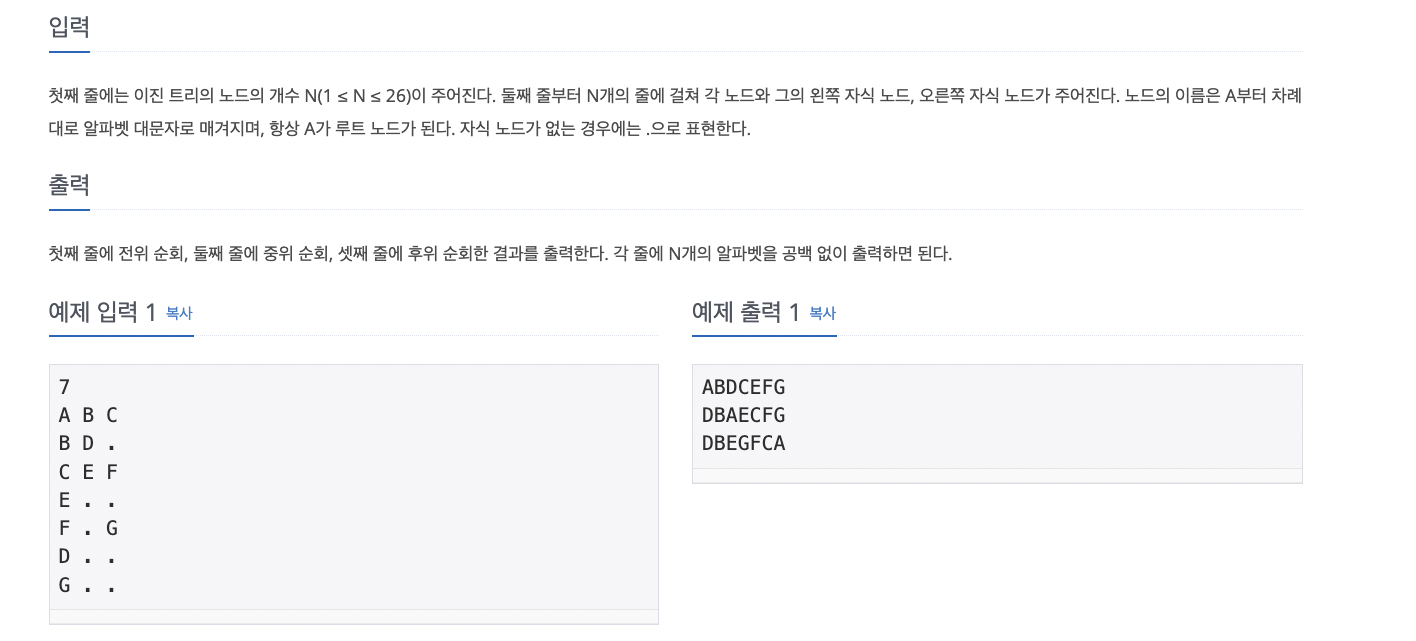
해당 문제는 이진트리의 순회과정을 코드로 구현하는 문제이다.
import sys
sys.stdin = open('input.txt', 'r')
input = sys.stdin.readline
class Node():
def __init__(self, item, left, right):
# item은 본인 (root node가 됨), left, right는 각각 child node가 됨.
self.item = item
self.left = left
self.right = right
# Node 생성 Node는 자기 자신의 값인 item과 child node의 위치인 left와 right를 가짐.
def preorder(node):
print(node.item, end='')
if node.left != '.':
preorder(tree[node.left])
if node.right != '.':
preorder(tree[node.right])
# 전위 순회 root > left child > right child 순으로 순회함.
def inorder(node):
if node.left != '.':
inorder(tree[node.left])
print(node.item, end='')
if node.right != '.':
inorder(tree[node.right])
# 중위 순회 left > root > right 순으로 순회함.
def postorder(node):
if node.left != '.':
postorder(tree[node.left])
if node.right != '.':
postorder(tree[node.right])
print(node.item, end='')
# 후위 순회는 left > right > root 순으로 순회함.
N = int(input())
tree = {}
# 노드를 엮어줄 트리 생성 딕셔너리로 받는 이유
# TypeError: list indices must be integers or slices, not str 때문.
for i in range(N):
node, left, right = map(str, input().split())
tree[node] = Node(node, left, right)
# 트리에 입력받은 노드 값 입력
# tree[A] = left, right, root node
preorder(tree['A'])
print()
inorder(tree['A'])
print()
postorder(tree['A'])해당 코드는 각각 전위, 중위, 후위 순회를 구현하였다. 재귀를 활용한 이유는 각 자식 노드들이 또다른 자식 노드들을 갖고 있을 때 다시 해당 노드들까지 탐색하도록 하기 위함이다.
출처)
https://www.youtube.com/watch?v=QN1rZYX6QaA&t=219s
https://www.youtube.com/watch?v=i5yHkP1jQmo
