Numeriacal Differention

Deleting the terms involving $\xi(x)$ gives

One difficulty with this formula is that we have no information about $D_x f^{\prime \prime}(\xi(x))$, so the truncation error cannot be estimated. When $x$ is $x_0$, however, the coefficient of $D_x f^{\prime \prime}(\xi(x)$ ) is 0 , and the formula simplifies to

For small values of $h$, the difference quotient $\left[f\left(x_0+h\right)-f\left(x_0\right)\right] / h$ can be used to approximate $f^{\prime}\left(x_0\right)$ with an error bounded by $M|h| / 2$, where $M$ is a bound on $\left|f^{\prime \prime}(x)\right|$ for $x$ between $x_0$ and $x_0+h$. This formula is known as the forward-difference formula if $h>0$ (see Figure 4.1) and the backward-difference formula if $h<0$.

Example

Use the forward-difference formula to approximate the derivative of $f(x)=\ln x$ at $x_0=1.8$ using $h=0.1, h=0.05$, and $h=0.01$, and determine bounds for the approximation errors.

Three-Point Endpoint Formula

$f^{\prime}\left(x_0\right)=\frac{1}{2 h}\left[-3 f\left(x_0\right)+4 f\left(x_0+h\right)-f\left(x_0+2 h\right)\right]+\frac{h^2}{3} f^{(3)}\left(\xi_0\right)$,
where $\xi_0$ lies between $x_0$ and $x_0+2 h$.

Three-Point Midpoint Formula

$f^{\prime}\left(x_0\right)=\frac{1}{2 h}\left[f\left(x_0+h\right)-f\left(x_0-h\right)\right]-\frac{h^2}{6} f^{(3)}\left(\xi_1\right)$

Five-Point Formulas

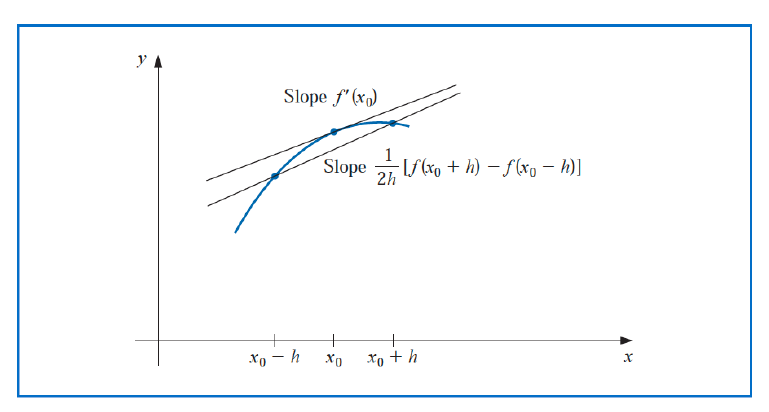
The methods presented in Eqs. (4.4) and (4.5) are called three-point formulas (even though the third point $f\left(x_0\right)$ does not appear in Eq. (4.5)). Similarly, there are five-point formulas that involve evaluating the function at two additional points. The error term for these formulas is $O\left(h^4\right)$. One common five-point formula is used to determine approximations for the derivative at the midpoint.

Five-Point Midpoint Formula

• $f^{\prime}\left(x_0\right)=\frac{1}{12 h}\left[f\left(x_0-2 h\right)-8 f\left(x_0-h\right)+8 f\left(x_0+h\right)-f\left(x_0+2 h\right)\right]+\frac{h^4}{30} f^{(5)}(\xi)$,
  where $\xi$ lies between $x_0-2 h$ and $x_0+2 h$.

Five-Point Endpoint Formula

where $\xi$ lies between $x_0$ and $x_0+4 h$.
Left-endpoint approximations are found using this formula with $h>0$ and right-endpoint approximations with $h<0$. The five-point endpoint formula is particularly useful for the clamped cubic spline interpolation of Section 3.5.

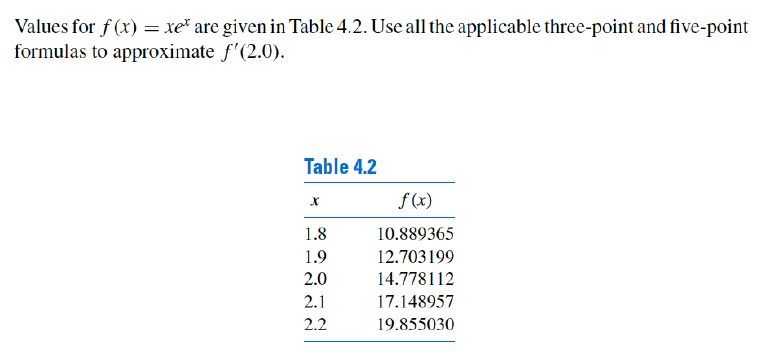
Example 2

Values for $f(x)=x e^x$ are given in Table $4.2$. Use all the applicable three-point and five-point formulas to approximate $f^{\prime}(2.0)$.

Second Derivative Midpoint Formula

for some $\xi$, where $x_0-h<\xi<x_0+h$.
If $f^{(4)}$ is continuous on $\left[x_0-h, x_0+h\right]$ it is also bounded, and the approximation is $O\left(h^2\right)$.

Example3

Round-Off Error Instability

It is particularly important to pay attention to round-off error when approximating derivatives. To illustrate the situation, let us examine the three-point midpoint formula Eq. (4.5),

more closely. Suppose that in evaluating $f\left(x_0+h\right)$ and $f\left(x_0-h\right)$ we encounter round-off errors $e\left(x_0+h\right)$ and $e\left(x_0-h\right)$. Then our computations actually use the values $\tilde{f}\left(x_0+h\right)$ and $\tilde{f}\left(x_0-h\right)$, which are related to the true values $f\left(x_0+h\right)$ and $f\left(x_0-h\right)$ by