5-1. Elementary Theory of Initial-Value Problems

Initial-Value Problems for ODEs : Elementary Theory of Initial-Value Problems

Elementary Theory of IVPs: Lipschitz Condition

We begin by presenting some definitions and results from the theory of ordinary differential equations before considering methods for approximating the solutions to initial-value problems.

우리는 초기 값 문제에 대한 솔루션을 근사화하는 방법을 고려하기 전에 일반 미분 방정식 이론의 일부 정의와 결과를 제시하는 것으로 시작한다.

Definition: Lipschitz Condition

A function $f(t, y)$ is said to satisfy a Lipschitz condition in the variable $y$ on a set $D \subset \mathbb{R}^2$ if a constant $L>0$ exists with

whenever $\left(t, y_1\right)$ and $\left(t, y_2\right)$ are in $D$. The constant $L$ is called a Lipschitz constant for $f$.

함수 $f(t, y)$는 집합 $D \subset \mathbb{R}^2$에서 변수 $y$의 립시츠 조건을 만족한다고 한다.상수 $L>0$이 있는 경우

$\left(t, y_1\right)$ 및 $\left(t, y_2\right)$가 $D$일 때마다.
상수 $L$는 $f$에 대한 립시츠 상수라고 한다.

Example

Show that $f(t, y)=t|y|$ satisfies a Lipschitz condition on the interval $D=\{(t, y) \mid 1 \leq t \leq 2$ and $-3 \leq y \leq 4\}$.

$f(t, y)=t|y|$가 $D=\{(t, y) \mid 1 \leq t \leq 2$ 및 $-3 \leq y \leq 4\}$ 구간에서 립시츠 조건을 만족함을 보여준다.

Solution

For each pair of points $\left(t, y_1\right)$ and $\left(t, y_2\right)$ in $D$ we have

Thus $f$ satisfies a Lipschitz condition on $D$ in the variable $y$ with Lipschitz constant 2. The smallest value possible for the Lipschitz constant for this problem is $L=2$, because, for example,

$D$의 각 포인트 쌍 $\left(t, y_1\right)$ 및 $\left(t, y_2\right)$에 대해 우리는 다음과 같은 것이 있다.

따라서 $f$는 Lipschitz 상수 2를 갖는 변수 $y$의 $D$에 대한 Lipschitz 조건을 만족시킨다. 예를 들어, 이 문제에 대해 립시츠 상수에 대해 가능한 가장 작은 값은 $L=2$이다.

Elementary Theory of IVPs: Convex Set

Definition: Convex Set

A set $D \subset \mathbb{R}^2$ is said to be convex if whenever $\left(t_1, y_1\right)$ and $\left(t_2, y_2\right)$ belong to $D$, then

also belongs to $D$ for every $\lambda$ in $[0,1]$.

집합 $D \subset \mathbb{R}^2$는 $\left(t_1, y_1\right)$와 $\left(t_2, y_2\right)$가 $D$에 속할 때마다 볼록하다고 한다.

또한 $[0,1]$의 모든 $\lambda$에 대해 $D$에 속한다.

Comment on the Definition

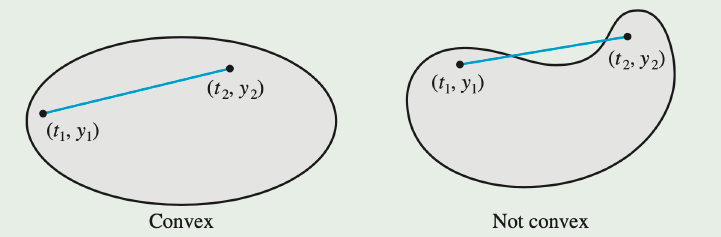
• In geometric terms, the definition states that a set is convex provided that whenever two points belong to the set, the entire straight-line segment between the points also belongs to the set.
• The sets we consider in this section are generally of the form
  $D=\{(t, y) \mid a \leq t \leq b \text { and }-\infty<y<\infty\}$
  for some constants $a$ and $b$.
• It is easy to verify that these sets are convex.

• 기하학적인 용어로, 두 점이 집합에 속할 때마다, 점 사이의 전체 직선 부분도 집합에 속한다고 가정하면, 집합은 볼록하다고 정의한다.
• 이 섹션에서 고려하는 집합은 일반적으로 다음과 같은 형식이다.
  $D=\{(t, y) \mid a \leq t \leq b \text { and }-\infty<y<\infty\}$
  일부 상수 $a$ 및 $b$의 경우.
• 이러한 집합이 볼록하다는 것을 쉽게 확인할 수 있다.

Theory of IVPs: Lipschitz Condition & Convexity

Theorem: Sufficient Conditions

Suppose $f(t, y)$ is defined on a convex set $D \subset \mathbb{R}^2$. If a constant $L>0$ exists with

then $f$ satisfies a Lipschitz condition on $D$ in the variable $y$ with Lipschitz constant $L$.

볼록 집합 $D \subset \mathbb{R}^2$에서 $f(t, y)$가 정의된다고 가정하자. 상수 $L>0$가 있는 경우

그런 다음 $f$는 Lipschitz 상수 $L$로 변수 $y$의 $D$에 대한 Lipschitz 조건을 만족시킨다.

Elementary Theory of IVPs

Theorem: Existence & Uniqueness

Suppose that $D=\{(t, y) \mid a \leq t \leq b$ and $-\infty<y<\infty\}$ and that $f(t, y)$ is continuous on $D$. If $f$ satisfies a Lipschitz condition on $D$ in the variable $y$, then the initial-value problem

has a unique solution $y(t)$ for $a \leq t \leq b$.

Note: This is a version of the fundamental existence and uniqueness theorem for first-order ordinary differential equations. The proof of the theorem, in approximately this form, can be found in Birkhoff, G. and G. Rota, Ordinary differential equations, (4th edition), John Wiley \& Sons, New York, 1989.

$D=\{(t, y) \mid a \leq t \leq b$와 $-\infty<y<\infty\}$가 $D$에 대해 연속적이라고 가정하자. $f$가 변수 $y$의 $D에 대한 립시츠 조건을 만족시킨다면, 초기 값 문제는 다음과 같다.

$a \leq t \leq b$에 대한 고유한 솔루션 $y(t)$가 있다.

참고: 이것은 1차 상미분 방정식의 기본 존재와 고유성 정리의 버전입니다. 이 정리의 증명은 버호프, G. 그리고 G. 로타, (4판), 존 와일리 &손스, 뉴욕, 1989에서 찾을 수 있다.

Example

Elementary Theory of IVPs: Well-Posed Problems

Question

How do we determine whether a particular problem has the property that small changes, or perturbations, in the statement of the problem introduce correspondingly small changes in the solution?

We first need to give a workable definition to express this concept.

특정 문제가 문제의 진술에서 작은 변화 또는 동요가 그에 상응하는 작은 변화를 가져오는 특성을 가지고 있는지 어떻게 결정하는가?

우리는 먼저 이 개념을 표현하기 위해 실행 가능한 정의를 내릴 필요가 있다.

Definition: Well-Posed Problem

The initial-value problem

is said to be a well-posed problem if the following 2 conditions are satisfied:

• A unique solution, $y(t)$, to the problem exists, and
• There exist constants $\varepsilon_0>0$ and $k>0$ such that for any $\varepsilon$, with $\varepsilon_0>\varepsilon>0$, whenever $\delta(t)$ is continuous with $|\delta(t)|<\varepsilon$ for all $t$ in $[a, b]$, and when $\left|\delta_0\right|<\varepsilon$, the initial-value problem
  $\frac{d z}{d t}=f(t, z)+\delta(t), \quad a \leq t \leq b, \quad z(a)=\alpha+\delta_0$
  has a unique solution $z(t)$ that satisfies
  $|z(t)-y(t)|<k \varepsilon \text { for all } t \text { in }[a, b] \text {. }$

초기값 문제

다음 두 조건이 충족될 경우 잘 해결된 문제라고 한다:

• 문제에 대한 고유한 솔루션 $y(t)$가 존재하며,
• $\varepsilon_0>0$ 및 $k>0$ 상수가 존재하며, $\varepsilon_0>\varepsilon>0$인 모든 $\varepsilon$에 대해 $\delta(t)|<\varepsilon$이 $[a, b]$의 모든 $t$에 대해 연속적이고 $\left|\delta_0|\right|\varepsilon$이 초기값이다.
  $\frac{d z}{d t}=f(t, z)+\delta(t), \quad a \leq t \leq b, \quad z(a)=\alpha+\delta_0$
  다음을 만족하는 고유한 솔루션 $z(t)$를 가지고 있다.
  $|z(t)-y(t)|<k \varepsilon \text { for } t \text { in }[a, b] \text {. }$