Lowest Common Ancestor (LCA)

LCA란 최소공통조상(Lowest Common Ancestor)을 찾는 알고리즘이다. 위 그림에서 2와 7의 최소공통조상은 1이다. LCA는 2와 7이 주어졌을 때 1을 찾는 알고리즘이라고 보면 된다!

구현

dfs

dfs 탐색을 통해 각 node의 depth와 부모 정보를 저장해준다.

void dfs(int n, int d){
    visit[n] = true; // visit 여부 update
    depth[n] = d; // depth 저장
    for(int i=0; i<v[n].size(); i++){
        int nextnode = v[n][i];
        if(!visit[nextnode]){ // 방문하지 않은 경우
            dp[0][nextnode] = n; // 부모(2^0 번째 조상) 정보 저장 
            dfs(nextnode, d+1); // 다음 노드 방문
        }
    }
}

setDP

DP를 이용하여 2^k번째 조상 노드 정보까지 저장해준다. 2^k번째 조상 노드 정보까지 저장하는 이유는 하나씩 일일이 탐색하지 않고, 2^k 씩 건너뛰면서 빠르게 탐색하기 위해서이다. node의 개수가 많아지는 경우 이렇게 하지 않으면 시간 내에 문제를 해결할 수 없다. 그 예가 바로 백준 11437번: LCA와 백준 11438번: LCA 2 이다. 두 문제를 다 풀어보면 왜 이런 방식을 사용하는지 이해할 수 있을 것이다!

• 백준 11437번: LCA 풀이
• 백준 11438번: LCA 2 풀이

void setDP(){
    for(int i=1; i<MAX_K; i++){
        for(int j=1; j<=N; j++){
            dp[i][j] = dp[i-1][dp[i-1][j]];
        }
    }
}

그림으로 나타내면 다음과 같이 작동하는 것이다!

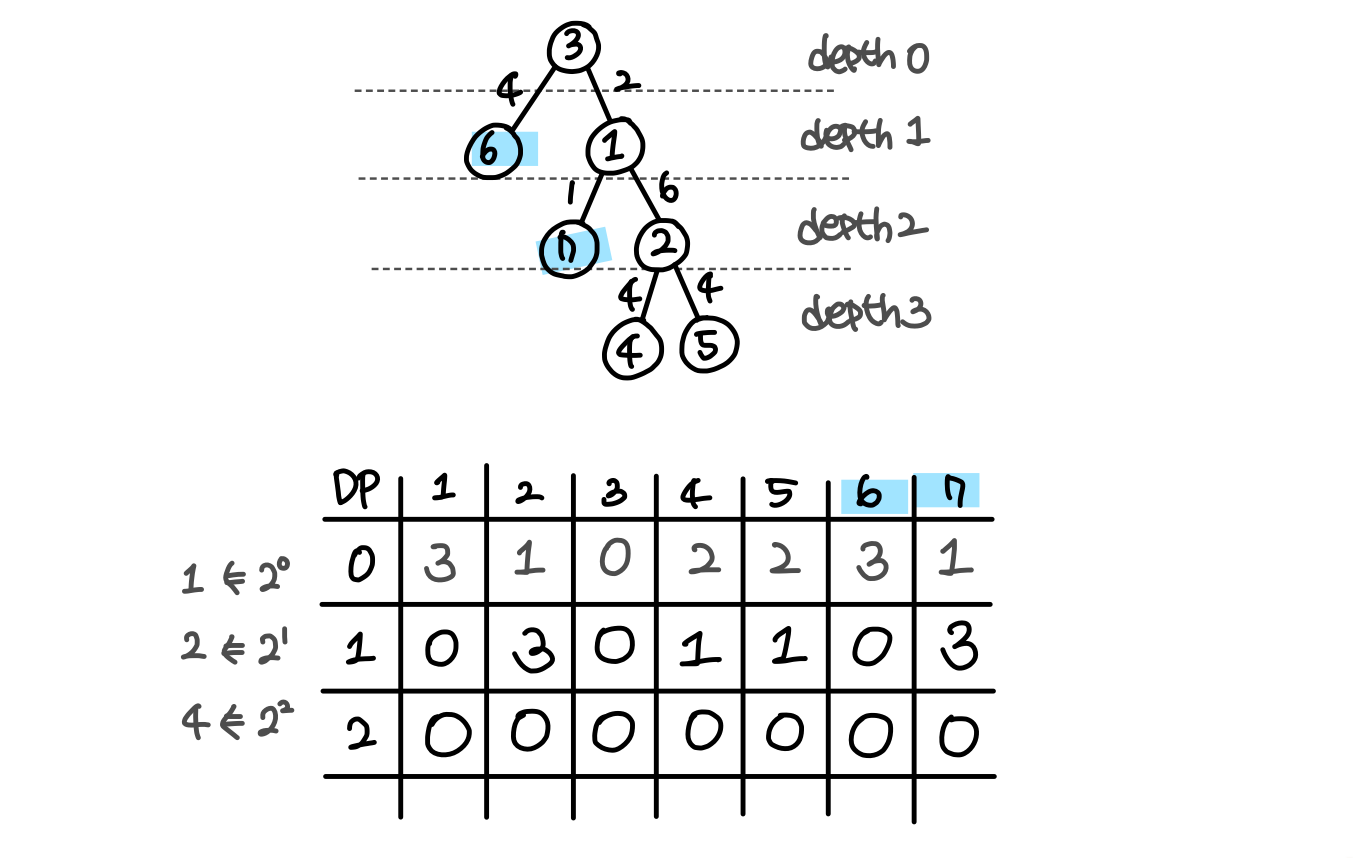
lca

저장해둔 depth와 2^k번째까지의 조상정보를 이용하여 LCA를 찾는 코드이다. 먼저 y가 더 깊음을 보장하기 위해 x가 더 깊은 경우 y와 swap을 해주었다. 이후 depth를 맞춰주고, 반복문을 돌면서 LCA를 찾아 주었다.

int lca(int x, int y){
    if(depth[y]<depth[x]) swap(x, y); // y가 더 깊음을 보장
    for(int i=MAX_K; i>=0; i--){
        if(depth[y]-depth[x] >= 1<<i) 
            y = dp[i][y]; // depth를 맞춰줌
    }
    if(x==y) return x; // x가 LCA(최소 공통 조상)인 경우
    for(int i=MAX_K; i>=0; i--){ // LCA를 찾음
        if(dp[i][x]!=dp[i][y]){ 
            x = dp[i][x];
            y = dp[i][y];
        }
    }
    return dp[0][x];
}

최종 코드

백준 11438번: LCA 2의 풀이다.

#include<iostream>
#include<cstring> // memset
#include<algorithm> // swap
#include<vector>
#define MAX_N 100001
#define MAX_K 17 // log2(MAX_N)
using namespace std;

int N, M, a, b;
int depth[MAX_N], dp[MAX_K+1][MAX_N];
bool visit[MAX_N];
vector<int> v[MAX_N];

void dfs(int n, int d){ // dfs 탐색을 통해 각 node의 depth와 부모 정보 저장
    visit[n] = true; // visit 여부 update
    depth[n] = d; // depth 저장
    for(int i=0; i<v[n].size(); i++){
        int nextnode = v[n][i];
        if(!visit[nextnode]){ // 방문하지 않은 경우
            dp[0][nextnode] = n; // 부모(2^0 번째 조상) 정보 저장 
            dfs(nextnode, d+1); // 다음 노드 방문
        }
    }
}

void setDP(){
    for(int i=1; i<MAX_K; i++){ // 2^k번째 조상 노드까지 저장
        for(int j=1; j<=N; j++){
            dp[i][j] = dp[i-1][dp[i-1][j]];
        }
    }
}

int lca(int x, int y){
    if(depth[y]<depth[x]) swap(x, y);
    for(int i=MAX_K; i>=0; i--){
        if(depth[y]-depth[x] >= 1<<i) 
            y = dp[i][y]; // depth를 맞춰줌
    }
    if(x==y) return x;
    for(int i=MAX_K; i>=0; i--){ // lca를 가질 때 까지 반복
        if(dp[i][x]!=dp[i][y]){ 
            x = dp[i][x];
            y = dp[i][y];
        }
    }
    return dp[0][x];
}

int main(){
    ios_base::sync_with_stdio(0); cin.tie(0);
    cin>>N;
    for(int i=0; i<N-1; i++){
        cin>>a>>b;
        v[a].push_back(b);
        v[b].push_back(a); // 트리는 무방향
    }
    memset(visit, false, sizeof(visit)); // false로 초기화
    dfs(1, 0); // tree의 root는 1번
    setDP(); // dp를 통해 2^k번째 조상 노드까지 저장
    cin>>M;
    for(int i=0; i<M; i++){
        cin>>a>>b;
        cout << lca(a,b) << '\n';
    }
}

관련 문제

백준 11438번: LCA 2, 백준 1761번: 정점들의 거리 등