시간 복잡도

n개의 입력 데이터에 대하여 알고리즘이 문제를 해결하는 데에 얼만큼의 시간이 걸리는지를 나타내는 것으로 점근적 표기법(asymptotic notation)을 사용

점근적 표기법(asymptotic notation) : 어떤 함수의 증가 양상을 다른 함수와의 비교로 표현하는 수론과 해석학의 방법 (= n이 충분히 큰 경우)

점근적 표기법 (asymptotic notation)

빅오 표기법 (Big-O Notation)

: 주어진 복잡도 함수 f(n)에 대하여 O(f(n))은 정수 N 이상의 모든 n에 대하여 g(n) <= c*f(n) 이 성립하는 양의 실수 c와 음이 아닌 정수 N이 존재하는 복잡도 함수 g(n)의 집합 (asymptotic upper bound)
g(n) ∈ O(f(n)) 이면, "g(n)은 f(n)의 Big-O 이다"라고 함

오메가 표기법 (Big-Ω Notation)

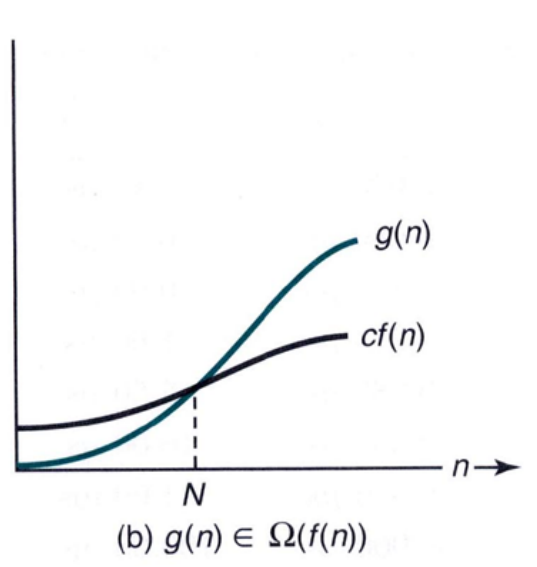: 주어진 복잡도 함수 f(n)에 대하여 Ω(f(n))은 정수 N 이상의 모든 n에 대하여 g(n) >= c*f(n) 이 성립하는 양의 실수 c와 음이 아닌 정수 N이 존재하는 복잡도 함수 g(n)의 집합 (asymptotic lower bound)
g(n) ∈ Ω(f(n)) 이면, "g(n)은 f(n)의 Ω이다"라고 함

세타 표기법 (Big-θ Notation)

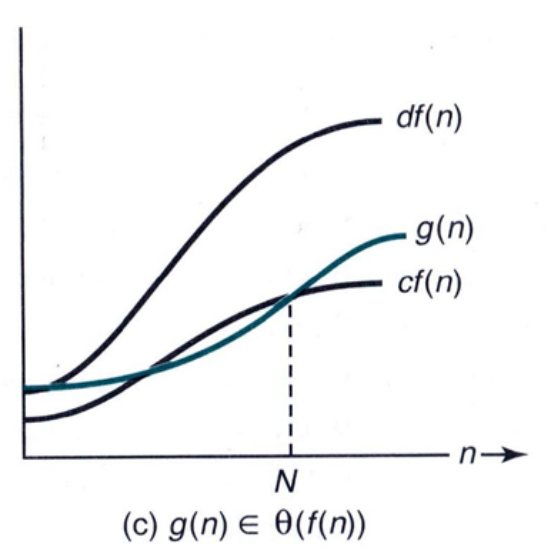: 주어진 복잡도 함수 f(n)에 대하여 θ(f(n))은 정수 N 이상의 모든 n에 대하여
c*f(n) <= g(n) <= d*f(n) 이 성립하는 양의 실수 c, d와 음이 아닌 정수 N이 존재하는 복잡도 함수 g(n)의 집합 (asymptotic tight bound)
g(n) ∈ θ(f(n)) 이면, "g(n)은 f(n)의 order(차수) 이다"라고 함