Segment Tree

세그먼트 트리: 주어진 데이터의 구간 합과 데이터 업데이트를 빠르게 수행하기 위한 자료구조. 이때 ‘구간 합’ 이라는 것은 합 배열을 뜻한다.

• 합 배열
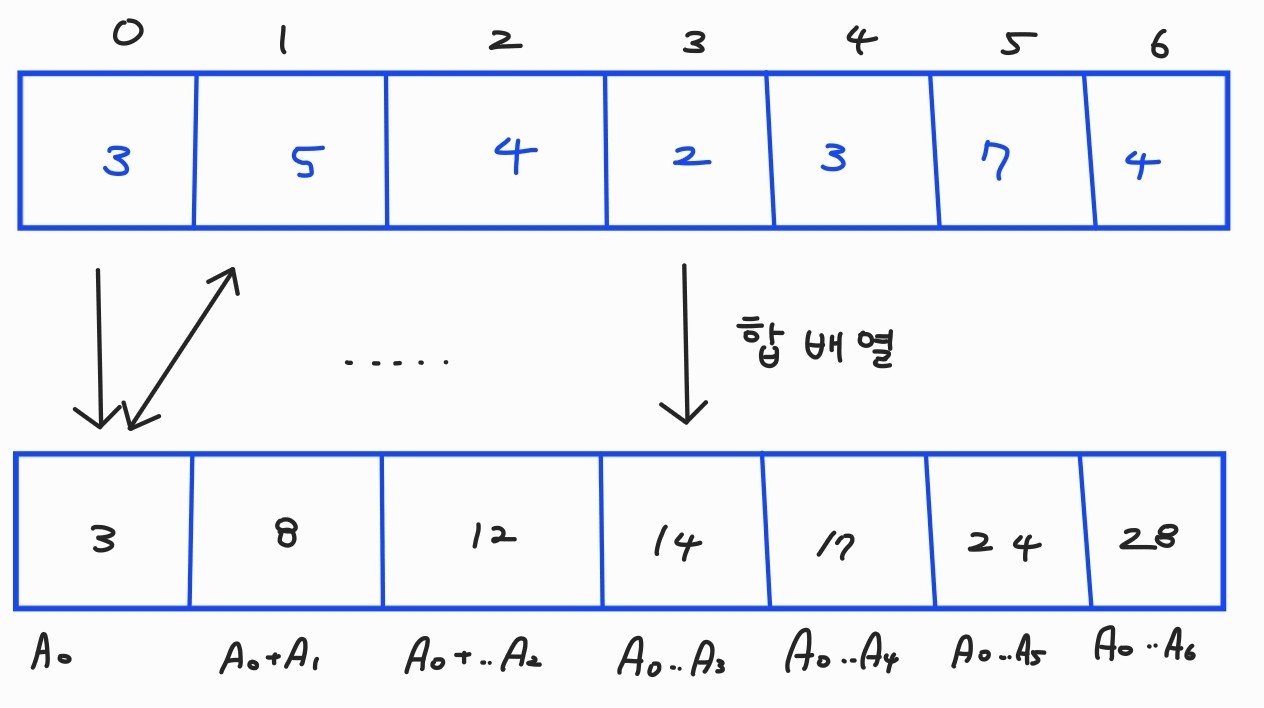
  • 다음은 합 배열을 구하는 과정이다
    

• 사진을보면 합 배열의 현재 인덱스 값을 그전의 인덱스 값을 모두 더한 것과 같다.

  

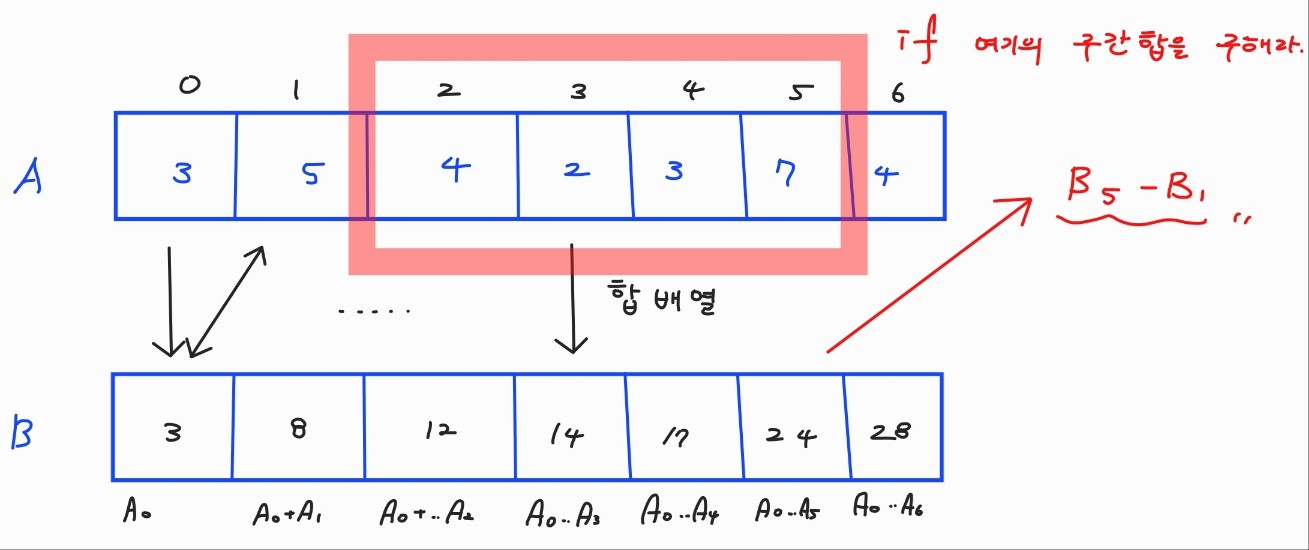
  • 이것을 활용한다면 위의 사진처럼 2~5 인덱스의 구간 합을 구하려면 합배열의 인덱스 5에서 1을 빼주면 된다.

• 왜 세그먼트 트리를 사용해야 될까?

  • 데이터의 업데이트의 문제가 발생! 합 배열의 데이터 업데이트가 굉장히 느리다
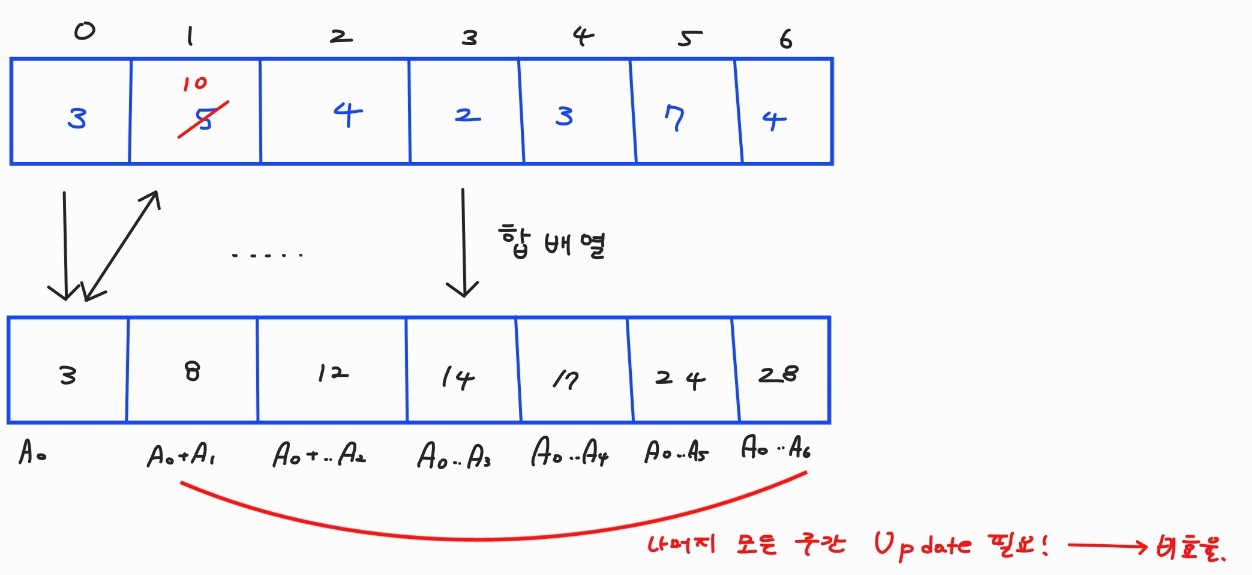
  • 따라서 데이터 업데이트가 훨씬 빠른 Segment Tree를 사용하게 된다.

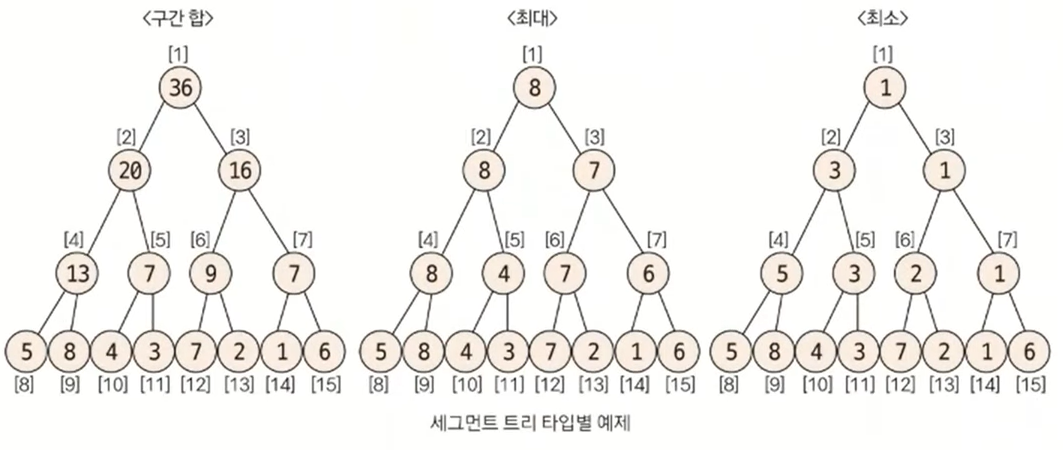
• 세그먼트 트리의 종류

  • 구간 합, 구간 곱, 구간의 최대 최소로 나뉜다.

• 세그먼트 트리 구현하기

  1. 트리 초기화 하기

     1. leaf 노드의 개수가 데이터의 개수(N) 이상이 되도록 트리 배열을 만든다.

     2. ex) Sample data → { 5, 8, 4, 3, 7, 2, 1, 6 }

        1. 트리의 크기를 구하는 방법
           1. 2^k≥N 을 만족하는 k의 최솟값을 구한 후 2^k*2 를 트리의 배열의 크기로 정의하면 된다
           2. N=8이므로 2^3≥8 이므로 배열의 크기는 2^3*2=16 으로 정의한다

     3. 트리의 leaf 노드에 원본 data가 들어간다. 이때 leaf 노드의 시작 위치를 찾아야 하는데, 구하는 방식은 2^k를 시작 인덱스로 취하면 된다. Sample data에서 k=3이므로 start index=8이 된다.

        

        

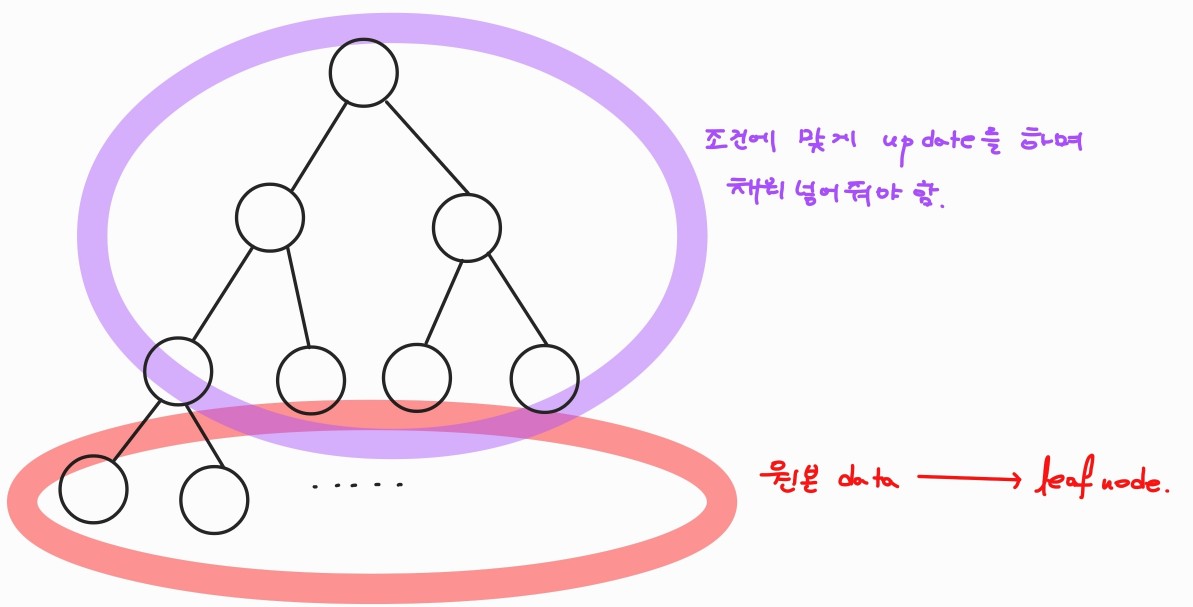
  2. 세그먼트 트리의 조건에 맞게 트리를 구성한다

     1. 구간 합

        

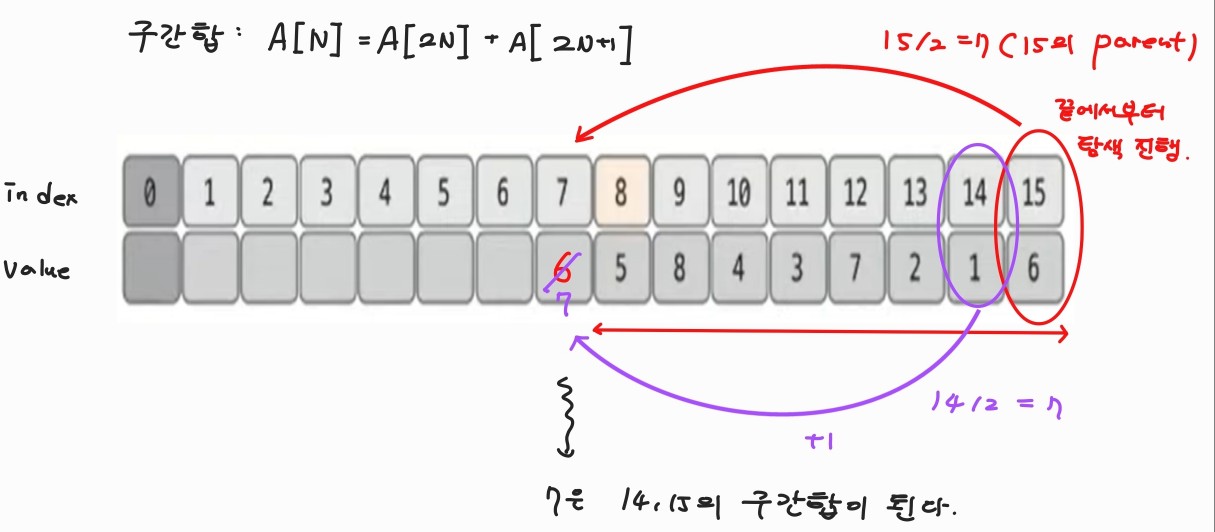
        1. 끝에서부터 탐색을 해주고, 구간 양쪽 자식의 합을 자신의 부모에 update하는 방식으로 root까지 진행한다.

           

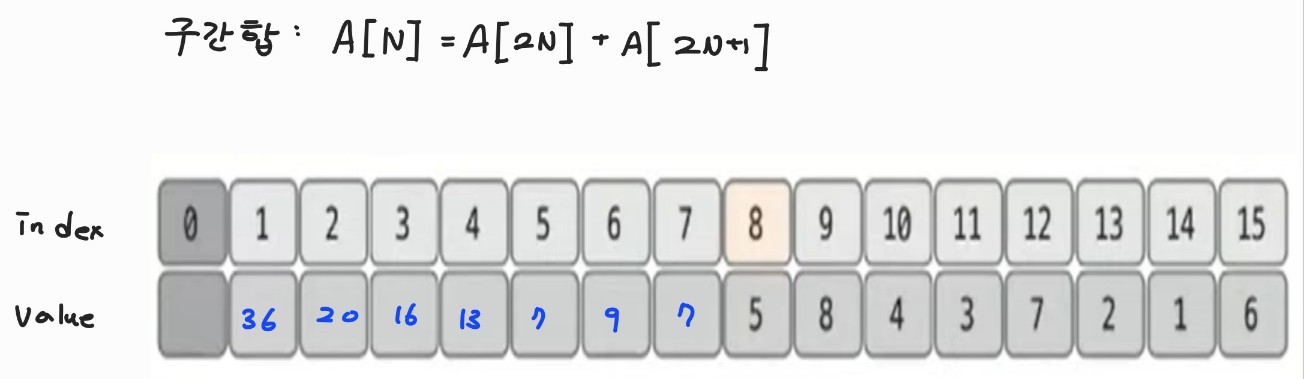
     2. 최대

        

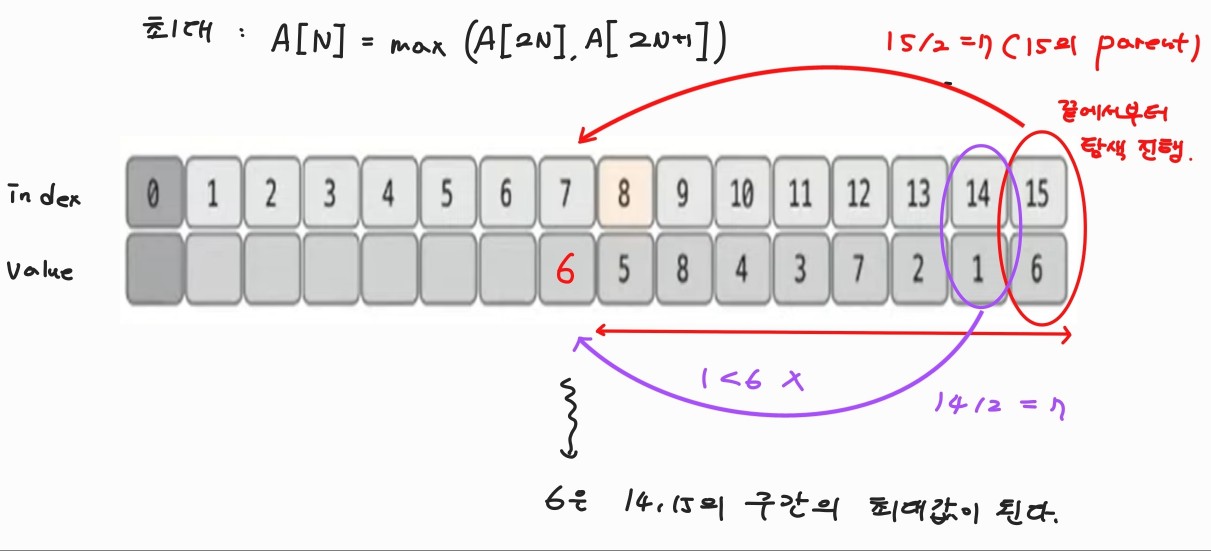
        1. 끝에서부터 탐색을 해주고, 구간 양쪽 자식중 큰 값을 자신의 부모에 update하는 방식으로 root까지 진행한다.

     3. 최소

        

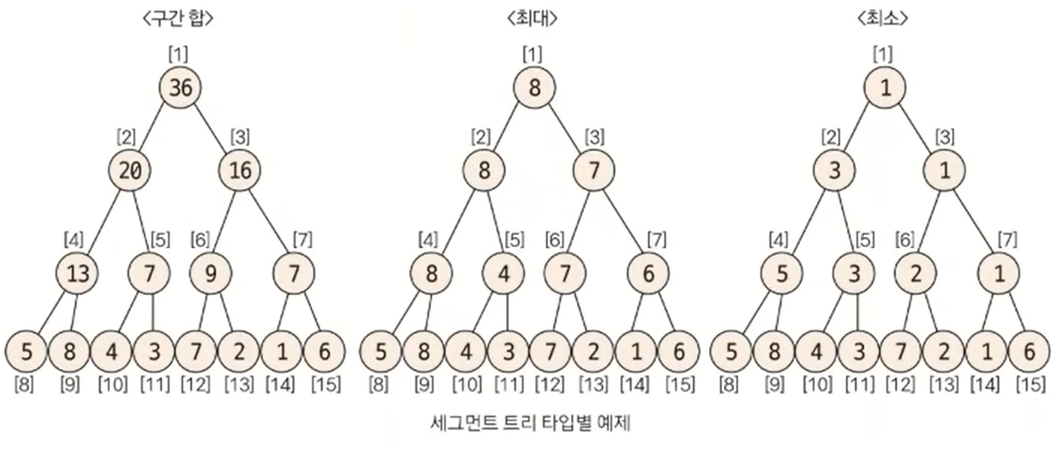
        1. 끝에서부터 탐색을 해주고, 구간 양쪽 자식 중 작은 값을 자신의 부모에 update하는 방식으로 root까지 진행한다.

  3. 주어진 쿼리 인덱스를 세그먼트 트리 인덱스로 변경하는 방법

     1. 세그먼트 트리 index = 주어진 질의 index + 2^k -1
     2. ex) 주어진 쿼리가 1~3이다
        1. 1+2^3-1 = 8
        2. 3+2^3-1 = 11
        3. 따라서 8~11이 된다.

  4. 쿼리값을 구하는 과정

     1. start_index % 2 == 1일 때 해당 노드를 선택한다.
     2. end_index % 2 == 0 일 때 해당 노드를 선택한다.
     3. start_index depth 변경 :( start_index + 1) / 2 연산을 실행한다.
     4. end_index depth 변경 : ( end_index - 1 ) / 2 연산을 실행한다.
     5. a, b에서 해당 노드를 선택했다는 것은 ****해당 노드의 부모가 나타내는 범위가 질의 범위를 넘어가기 때문에 해당 노드를 질의 값에 영향을 미치는 독립 노드로 선택하고,**** 해당 노드의 부모 노드는 대상 범위에서 **제외한다는 뜻**이다. 부모 노드를 대상 범위에서 제거하는 방법은 c, d 에서 질의 범위에 해당하는 부모 노드로 이동하기 위해 인덱스 연산을 index / 2 가 아닌 (index+1)/2, (index-1)/2로 수행하는 것이다.
     6. 질의에 해당하는 노드를 선택하는 방법은 구간 합, 최대 최소 값 구하기 모두 동일하며 선택된 노드들에 관해 마지막에 연산하는 방식만 다르다.