Context-Free Grammars(2)

Parse Trees and Derivations

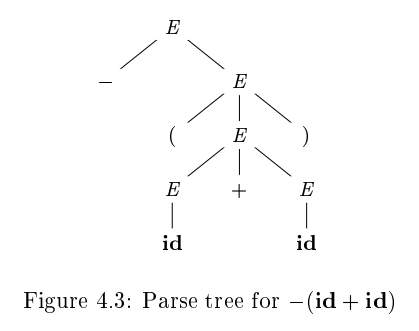
• 대충 요런 느낌. leaf node를 왼쪽부터 순서대로 읽어가면 sentential이 나온다. 이를 $yield$ or $frontier$ of the tree라고 부른다.

• derivation과 parse tree 사이의 관계

  • consider any derivation $\alpha_1\Rightarrow\alpha_2\Rightarrow\cdots\Rightarrow\alpha_n$, where $\alpha_1$ is a single nonterminal $A$.
  • 결국 이 derivation은 inductively하게 parse tree를 구성하면 만들 수 있다.

• BASIS : $\alpha_1 = A$의 tree는 $A$라고 쓰인 single node이다.

• INDUCTION
  

• 위 방법은 derivation들과 parse tree간의 다대일 관계를 만들게 된다.

• leftmost 또는 rightmost derivations은 parse tree와 일대일 대응 관계를 가지고 있다.
  -> 나름 쉽게 증명가능.

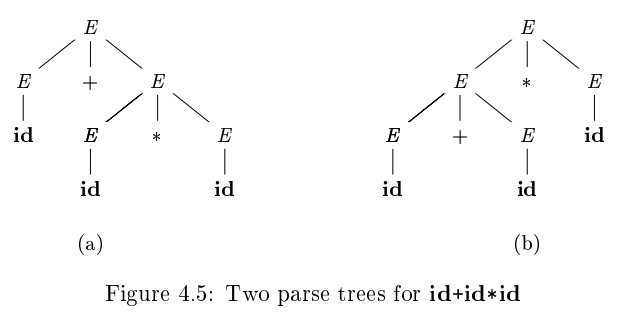
Ambiguity

• 둘 이상의 parse tree를 만드는 sentence가 존재하면 그 grammar를 $ambiguous$하다고 말한다.
• 다른 말로, 둘 이상의 leftmost derivation이나 rightmost derivation을 통해서 같은 sentence를 만들 수 있는 경우 grammar를 ambiguous하다고 한다. (위 문장과 동치)
• ex)
  
  

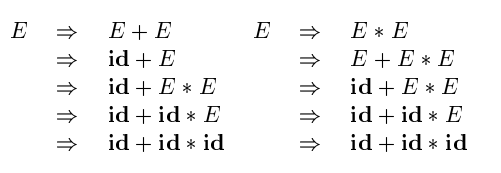
Verifying the Language Generated by a Grammar

• grammar $G$가 language $L$을 generate한다는 것을 증명하는 방법

  • $G$에 의해 만들어지는 모든 string이 $L$의 원소임을 보인다.
  • 모든 $L$의 원소가 $G$에 의해 만들어질 수 있다.

• Example 4.12) Consider the following grammar:

  $S\rightarrow(\,S\,)\,S\,|\,\epsilon$

• $(\Rightarrow)$ : every sentence derivable from $S$ is balanced.

  • induction 사용 : "n번 derive를 통해 나온 sentence는 balanced이다."
    • BASIS : The basis is $n=1$. -> 1번 derive를 통해 나온 sentence는 $\epsilon$밖에 없고, 이는 당연히 balanced이다.
    • INDUCTION : assume that all derivations of fewer than $n$ steps produce balanced sentences. 그리고 정확히 n step을 거친 leftmost derivation을 고려해 보자. (어떤 derivation이든 간에 leftmost derivation으로 유도가 가능하다.) 그러한 derivation은 다음과 같은 형태이다 :
      $S\underset{lm}\Rightarrow\,(S)S\overset{*}{\underset{lm}\Rightarrow}\,(x)S\overset{*}{\underset{lm}\Rightarrow}\,(x)y$
      $x$와 $y$의 derivation은 $n$ step보다 더 적다. 그러므로 inductive hypothesis에 의해서 $x$, $y$는 balanced이다. 그러므로 string $(x)y$ 또한 balanced이다.

• $(\Leftarrow)$ : every balanced string is derivable from $S$.
  use induction on the length of a string.

  • BASIS : If the string is of length 0, it must be $\epsilon$, which is balanced.
  • INDUCTION : Note that every balanced string has even length.
    induction hypothesis : 길이가 $2n$보다 작은 모든 balanced string이 $S$로부터 derivable하다고 가정하자.
    길이 $2n\,,n\geq 1$인 balanced string $w$를 고려하자.
    $w$는 당연히 (로 시작할 것이다.
    $(x)$를 같은 수의 (와 )를 갖고 있는 shortest nonempty prefix of $w$ 라고 하자.
    그러면 $w=(x)y$로 쓸 수 있고, $x$와 $y$는 각각 balanced인 길이 $2n$보다 작은 string이므로 induction hypothesis에 의해 각각은 $S$로 부터 derivable하다.
    결국
    $S\Rightarrow\,(S)S\overset{*}\Rightarrow\,(x)S\overset{*}\Rightarrow\,(x)y$
    가 되어 $S$로 부터 derivable하다.

Context-Free Grammars Versus Regular Expressions

• 모든 regular expression은 grammar로 표현이 가능하지만, 반대는 불가능하다.
• 즉, 모든 regular language는 context-free language이지만, 반대는 아니다.
• 예를 들어, regular expression (a$|$b)$^*$abb와 grammar
  $A_0\rightarrow aA_0|bA_0|aA_1 \\ A_1\rightarrow bA_2 \\ A_2\rightarrow bA_3 \\ A_3\rightarrow\epsilon$

  는 $abb$로 끝나는 같은 language를 표현한다.

• NFA가 의미하는 것과 동일한 language를 표현하는 grammar를 만드는 방법이 존재한다.
  1. NFA의 각 state $i$에 대해 nonterminal $A_i$를 만든다.
  2. state $i$가 input $a$에 대해 state $j$로의 transition이 존재하면, production $A_i\rightarrow aA_j$를 추가한다. 만약 state $i$가 input $\epsilon$에 대해 state $j$로 한다면, production $A_i\rightarrow A_j$를 추가한다.
  3. 만약 $i$가 accepting state라면, $A_i\rightarrow\epsilon$을 추가한다.
  4. 만약 $i$가 start state라면, $A_i$를 grammar의 start symbol로 정한다.
• 반대로, language $L=\{a^nb^n\,|\,n\geq1\}$는 grammar로는 표현이 가능하지만 regular expression으로는 표현이 불가능하다.
  • $L$이 grammar로 표현이 가능한 이유
    $S\rightarrow aFb \\ F\rightarrow S|\epsilon$
  • 귀류법으로 증명 : $L$이 regular expression으로 표현이 가능하다고 가정. 그러면 이를 $k$개의 state를 가진 DFA $D$가 표현가능하다고 할 수 있다.
    
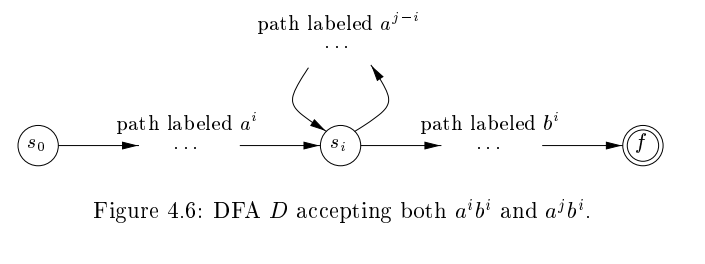
    • 위 사진을 보면 더 이해가 잘 된다.
    • k보다 더 큰 $a^nb^n$을 생각해 보자. 그러면 이 녀석은 a만 해도 n번의 이동을 할 텐데, 애초에 state 수가 k보다 더 크므로 언젠간 같은 state를 지나게 될 것이고, 그 state를 처음으로 지났을 때 $i$번 움직인 것이라고 하고, 다시 지났을 때를 $j$번 움직인 것이라고 하자. 그리고 그 state를 $s_i$라고 하자.
    • $a^ib^i$ 또한 $L$에 포함되므로 $s_i$ state에서 final state까지 $b^i$를 통해서 가는 어떤 경로가 존재할 것이다.
    • 그렇다면 결국 $a^j$만큼 움직인 후 $s_i$ state에서 final state로 $b^i$만큼 움직여서 갈 수 있으므로 $a^jb^i$ 또한 $L$의 원소가 되는데, 이는 $L$의 정의에 모순이 된다.
    • 그러므로 $L$은 regular expression으로 표현이 불가능하다.
• 정리
  • "finite automata cannot count" : b를 보기 전에 a의 숫자를 count해야 하는 경우 동작 못함.
  • "grammar can count two items but not three"