Top-Down Parsing(1)

Recursive-Descent Parsing

• left-recursive grammar는 recursive-descent parser로 하여금 무한루프를 돌게 만들 수 있다.

FIRST and FOLLOW

• $Def.$
  • $FIRST(\alpha)$ : $\alpha$는 grammar symbol들의 string이라고 할 때, $\alpha$로 부터 derive된 strings 중 begin terminal들의 집합.
  • $FOLLOW(A)$ : $A$를 nonterminal이라고 할 때, the set of terminals $a$ such that there exists a derivation of the form $S\overset{*}\Rightarrow\alpha Aa\beta$, for some $\alpha$ and $\beta$
    
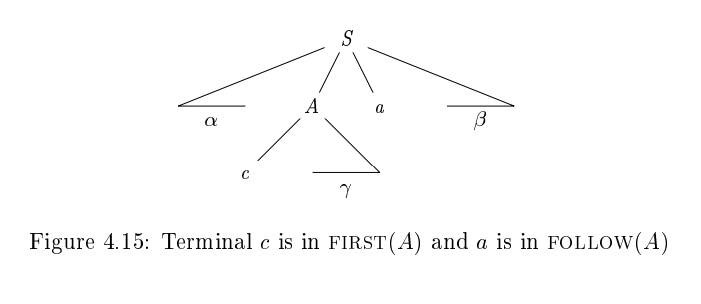
• 참고로 $A$와 $a$ 사이에 symbol이 있었을 수도 있었겠지만, $\epsilon$으로 사라졌을 것이고, 만약 $A$가 제일 오른쪽에 위치해 있었다면 ${\$}$(endmarker symbol) 또한 $FOLLOW(A)$의 원소가 된다.
• 각 grammar symbol X에 대한 FIRST(X) 계산하는 방법 : 아래 방법을 어떤 terminal이나 $\epsilon$이 FIRST set에 포함되지 않을 때 까지 적용시킨다.
  1. If X is a terminal, then FIRST(X) = {X}
  2. If X is a nonterminal and $X\rightarrow Y_1Y_2\cdots Y_k$ is a production for some $k\geq 1$일 때,
     $a\in FIRST(X)$ 라는 것은 FIRST($Y_1$), ..., FIRST($Y_{i-1}$)까지 모두 $\epsilon$을 원소로 포함하고 있고, $a\in FIRST(Y_i)$인 i가 존재한다는 뜻이다.
     만약 모든 j = 1, 2, ..., k에 대해서 $\epsilon\in FIRST(Y_j)$라면 $\epsilon\in FIRST(X)$이다.
  3. If $X\rightarrow\epsilon$ is a production, then add $\epsilon$ to FIRST(X).

-> 어떠한 string $X_1X_2\cdots X_n$에 대해서 FIRST를 구할 수 있다.

• FOLLOW(A) 구하는 방법 : FOLLOW set에 어떤 원소도 들어가지 않을 때 까지 아래를 반복.
  1. start symbol $S$에 대해 $\$$를 FOLLOW(S)에 넣는다. 그리고 $\$$는 input의 마지막에 들어가는 marker이다.
  2. $A\rightarrow\alpha B\beta$가 존재하면, $\epsilon$을 제외한 모든 FIRST($\beta$)의 원소가 FOLLOW(B)의 원소이다.
  3. $A\rightarrow\alpha B$나 $A\rightarrow\alpha B\beta$, where $\epsilon\in FIRST(\beta)$가 존재하면, FOLLOW(A)의 모든 원소는 FOLLOW(B)의 원소이다.

LL(1) Grammars

• recursive-descent parser인데 backtracking을 필요로 하지 않는 Predictive parser는 LL(1)이라고 불리는 grammar들의 class로 만들어질 수 있다.

• LL(1) : scanning input from left to right, leftmost, 뒤의 1개의 input symbol로 판별.
  
  

• A grammar $G$ is LL(1) if and only if whenever $A\rightarrow\alpha\,|\,\beta$ are two distinct productions of $G$, the following conditions hold:
  

  • 1, 2번 : FIRST($\alpha$)와 FIRST($\beta$)는 disjoint sets와 동치.
  • 3번 : 만약 $\epsilon$이 FIRST($\beta$)안에 있다면, FIRST($\alpha$)와 FOLLOW(A)는 disjoint set이라는 뜻. 만약 $\epsilon$이 FIRST($\alpha$)안에 있다면 FIRST($\beta$)와 FOLLOW(A)는 disjoint set이라는 뜻.

• Predictive parser는 LL(1) grammar에 대해 만들어질 수 있는데, 그 이유는 아래와 같다.
  
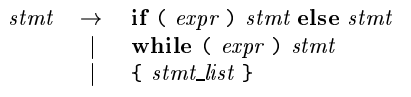
  하나의 symbol만 체크해서 다음 production이 무엇인지를 선택해야 하는데, 위의 예시의 경우 if / whlie / { 인지에 따라 바로 결정이 되는 LL(1)에 해당하기 때문에 굉장히 편리하다.

• FIRST와 FOLLOW로부터 2차원 배열인 predictive parsing table M\[A,a\]를 만들 수 있다. (A : nonterminal, a : terminal이거나 symbol $\$$)

• 알고리즘의 아이디어 :
  만약 다음 input symbol a가 FIRST($\alpha$)의 원소라면 $A\rightarrow\alpha$가 선택된다.
  만약 $\alpha\overset{*}\Rightarrow\epsilon$이라면, 현재 input symbol이 FOLLOW(A)에 있거나 $\$$에 도달했고 FOLLOW(A)에 있다면 $A\rightarrow\alpha$를 선택한다.

• Algorighm 4.31 : Construction of a predictive parsing table

  • INPUT : Grammar $G$
  • OUTPUT : Parsing table $M$
  • METHOD : For each production $A\rightarrow\alpha$ of the grammar, do the following:
    1. FIRST($\alpha$)의 각 terminal $a$에 대해 M\[A,a\]에 $A\rightarrow\alpha$를 추가한다.
    2. $\epsilon$이 FIRST($\alpha$)안에 있다면, FOLLOW(A)의 각 terminal $b$에 대해 $A\rightarrow\alpha$를 M\[A,b\]에 추가한다.
       만약 $\epsilon$이 FIRST($\alpha$)에 있고 $\$$가 FOLLOW(A)에 있다면, $A\rightarrow\alpha$를 M\[A,\$\]에 추가한다.
    • 만약 위 방법이 끝나고 나서 M\[A,a\]에 아무런 production도 없다면, M\[A,a\]를 error 상태로 둔다.

• LL(1) grammar의 경우, 각 parsing-table entry에는 unique한 production 혹은 error만 존재한다.

• 다른 grammar의 경우, 한 entry에 여러 production이 존재할 수도 있다.