1. 나머지 연산(Modular Arithmetic)
컴퓨터의 정수는 저장할 수 있는 범위가 저장되어있기 때문에, 답을 M으로 나눈 나머지를 출력하라는 문제가 등장한다.
- (A + B) mod M = ((A mod M) + (B mod M)) mod M
- (A B) mod M = ((A mod M) (B mod M)) mod M
- 나누기의 경우 성립하지 않는다.(Modular Inverse를 구해야 함.)
(6 / 3) % 3 = 2 % 3 = 2 ((6 % 3) / (3 % 3)) % 3 = (0/0) % 3 = 0- 뺄셈의 경우에는 먼저 mod 연산을 한 결과가 음수로 나올 수 있기 때문에 다음과 같이 해야한다.
(A - B) mod M = ((A mod M) - (B mod M) + M) mod M
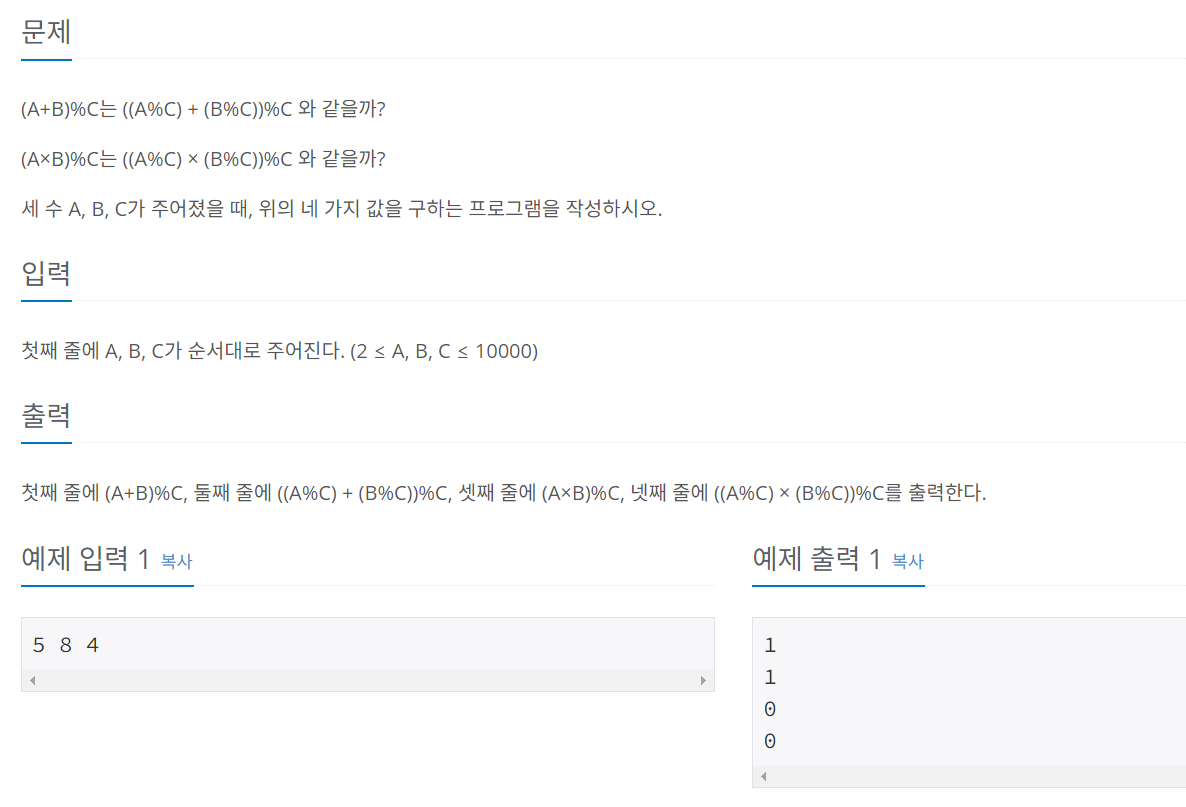
연습문제(1) : 백준 10430번
간단한 구현문제이다. 해당 조건에 따라 코딩하여 결과를 보면 된다.
실제로 더하기, 곱하기의 경우 mod 연산의 분배법칙이 적용되는 것을 확인할 수 있다.
문제에서 "정답을 ~~로 나눈 나머지를 출력하라" 라는 말이 있는 이유는 정답이 int나 long long과 같은 자료형의 범위를 넘어가기 때문이다.
그럼 음수가 나오는 경우는 어떨까?
(6 - 5) % 3 = 1 % 3 = 1 이다.
(6 % 3 - 5 % 3) % 3 = (0 -2) % 3 = -2 % 3 = ????
음수의 경우 결과의 부호가 프로그래밍 언어마다 다르다.
(참고 : https://en.wikipedia.org/wiki/Modulo)
(6 % 3 - 5 % 3) % 3 = ????
- C11, C++14 : -2
- Java : -2
- Python3 : 1
왜 이렇게 되는지, 해당 document를 읽어도 이해가 되지 않아 더 찾아보았다.
결론은, 각 case에 따른 해석의 차이라고 할 수 있다. C, C++, Java의 경우 첫번째 방식을 따르고, Python의 경우 후자의 방식을 따른다고 볼 수 있다. 크게 혼동할 것은 없고, 프로그래밍 언어가 어떤 방식을 따르는지에 따라 결과가 달라질 수 있다는 것을 유념하자.
2. 최대공약수(Greatest Common Divisor)
- 최대공약수는 줄여서 GCD라고 쓴다.
- 두 수 A와 B의 최대공약수 G는 A와 B의 공통된 약수 중에서 가장 큰 정수이다.
- 최대공약수를 구하는 가장 쉬운 방법은 2부터 min(A, B)까지 모든 정수로 나누어보는 방법이다.
- 최대공약수가 1인 두 수를 서로소(Coprime)라고 한다.
#include <iostream>
using namespace std;
int main(){
int A,B;
cin >> A >> B;
int G = 1;
for(int i = 2; i <= min(A, B); i++){
if((A % i == 0) && (B % i == 0)){
G = i;
}
}
cout << G << endl;
return 0;
}위는 내가 직접 GCD를 구해보았다. 민망하지만, if문 안에 '%'가 아닌 '/'를 사용하여 계속해서 결과가 1이 나와 5분정도 당황했었다. but, 중요한것은 이 방법보다 더 빠른 방법이 있다는 것이다.
유클리드 호제법(Euclidean algorithm)
- a를 b로 나눈 나머지를 r이라고 했을 때,
- GCD(a,b) = GCD(b,r)과 같다.
- r이 0이면, 그 때 b가 최대 공약수이다!
- GCD(24,16) = GCD(16,8) = GCD(8,0) = 8
#include <iostream>
using namespace std;
int GCD(int a, int b){
while(b != 0){
int r = a % b;
a = b;
b = r;
}
return a;
}
int main(){
int A,B;
cin >> A >> B;
cout << GCD(A, B);
return 0;
}위는 유클리드 호제법을 함수로 구현한 것이다. 그렇게 어렵지 않으니 코드를 보지말고 해당 조건들을 바탕으로 코딩해보는 것을 추천한다. 또, 해당 코드를 재귀함수로 구현할 수 있는데,
int GCD(int a, int b){
if (b == 0){
return a;
}
else {
return GCD(b, a % b);
}
}이렇게 구현할 수 있다.
하지만, 갑자기 재귀로 짜보려니 생각보다 힘들었다..
오늘의 총평
모든 개념과 예시들이 나에게 '1+1은 왜 2일까?'라는 질문을 하는 것과 같았다.
사고력이 많이 부족한 것인지, 펜을 드려는 용기가 부족한 것인지..
확실한 것은 전공자라면 답이 틀렸던, 맞았던 대답은 할 수 있어야한다. 하지만 난 그러지 못했다.
오늘은 유클리드 호제법을 이해한 후 마무리 하려 한다.