블로그에 포스팅하는 내용들은 강의 전체 내용이 아닌 내 기준, 나한테 필요한 내용들 기억하고 싶은 내용들 위주입니다
해당 내용의 출처는 LG Aimers(https://www.lgaimers.ai)에 있습니다
Part 1. 순환 신경망 기반의 시계열 데이터 회귀
Non-Sequential Data : 시간 정보를 포함하지 않고 생성되는 데이터
- N by D 행렬로 표현 (N : 관측치 수, D : 변수 수)
- 테이블, 행렬 형태
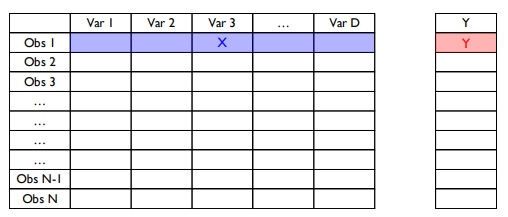
x : 첫 번째 관측치의 하나의 vector
y : 그에 대응하는 하나의 scalar
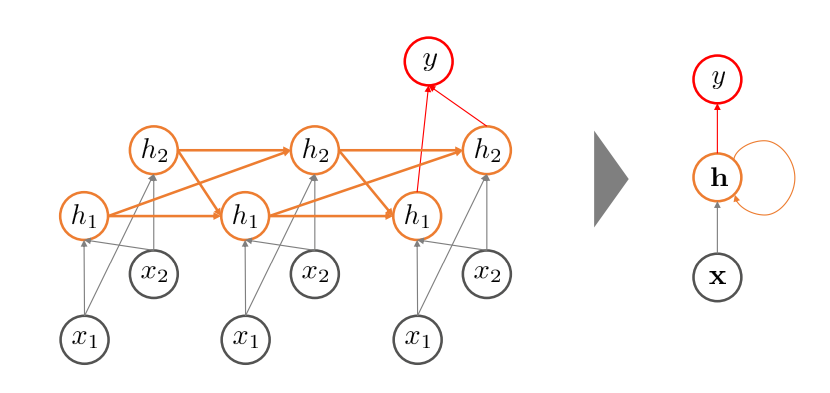
Non-Sequential한 인공 신경망 구조
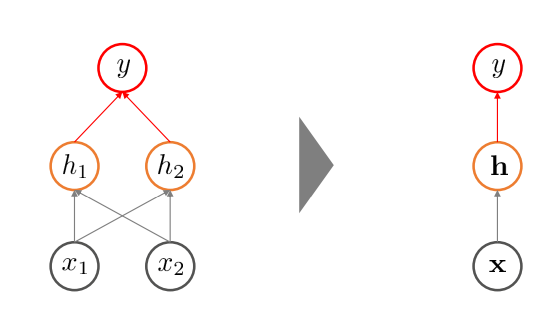
회색 : 설명 변수
주황 : hidden node
빨강 : output
- 왼쪽 그림을 vector 형식으로 표현하면 오른쪽 그림
- 순서가 없는 인공신경망의 경우, x->h->y 방향 화살표만 존재함
Sequential Data :시간 정보를 포함하여 순차적으로 생성되는 데이터
- (N) by T by D Tensor/Array (T는 측정 시점 수)로 표현
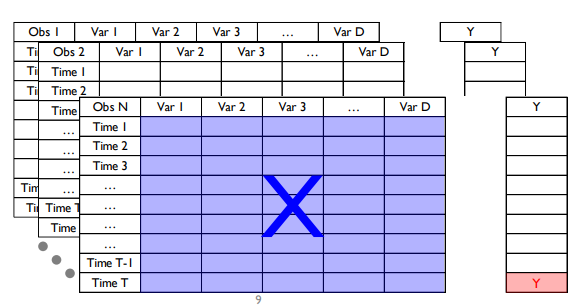
관측치 하나에 대해서 하나의 행렬이 나오게 됌
- 행 : Time 1 ~ Time T
- 열 : 변수 1 ~ 변수 D
즉 T by D 차원
하나의 무언가에(N개) 대해서 시점별로 수집되는 Data
이 행렬을 설명 변수 X 라고 두고, 그에 대응하는 critical dimension y를 예측하게 됌
N개의 관측치들에 대해서 각각의 관측치들은 T 차원의 시점 벡터를 갖으며 D 차원의 변수 크기를 갖게 됌
Sequential한 인공신경망 구조
순차적으로 설명 변수가 투입됌
이전 시점의 hidden node의 정보가 다음 시점의 hidden node 정보로 연결됌 = 과거의 정보가 누적되어 전달됌
h->h 구조가 존재함 => 순환 신경망
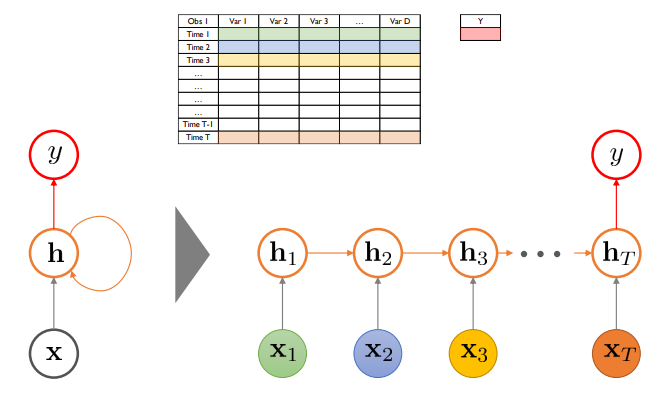
이러한 구조를 Vanilla RNN이라 함
RNN Basics
Foward Path
기본 RNN(Vanilla RNN) 구조

가장 중요한 부분 -> ht
t 시점에서의 hidden node의 값(ht)은 두 방향에서 정보를 전달받음
- t-1 시점의 hidden node에 저장된 정보
- t 시점에서 새롭게 제공되는 input
위에서 색으로 표시된 W 수식 : 학습되는 대상 즉 모델의 파라미터 (모델 학습을 통해 최적으로 찾아가야하는 값)
Gradient Vanishing / Exploding Problem
활성화 함수 f : 줄여서 Tanh(hyperbolic tangent)
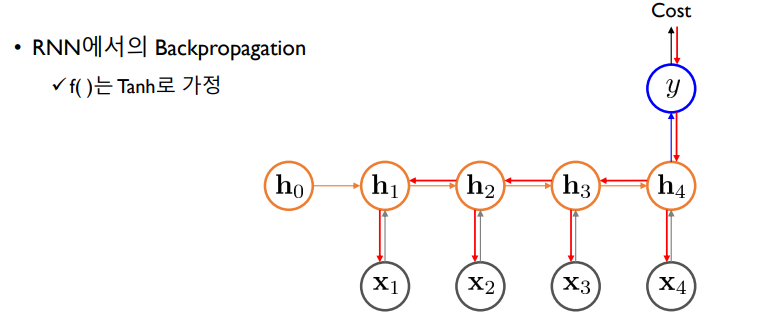
back propagation : 실제로 얼마만큼 틀렸는지를 계산한 후에(Cost) 역방향으로 어떻게 해야 입력과 출력 쌍을 잘 맞출 수 있는지 가중치 행렬을 구하는 것
즉 입력층과 hidden층 사이의 정보인 Wxh를 최적화하는 것
Wxh는 빨간 화살표 연산에 모두 해당함
따라서 back propagation을 하려면 Wxh 부분을 모두 편미분을 통해 해당하는 gradient가 무엇인지 찾아야함
이 gradient를 찾는 방식은 역방향으로 cost를 y에 대해 미분 -> y를 h4에 대해 미분 -> h4를 Wxh에 대해 미분 => Cost부터 x4까지 화살표에 의해 나오는 정보가 전달 ~
(수식 생략)
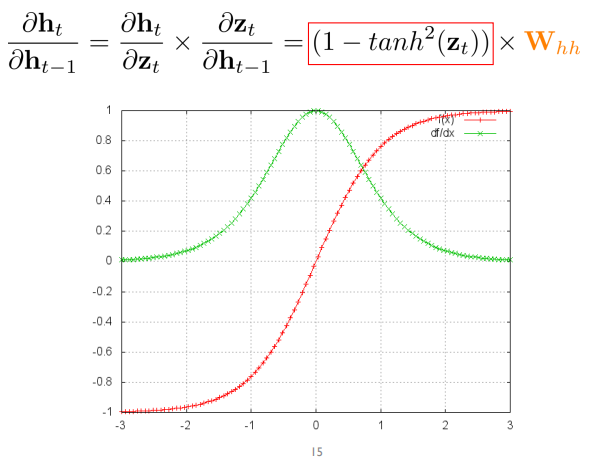
빨간색 그래프가 tanh(x)
초록색 그래프가 1-tanh^2(x)
즉 특정 값을 벗어나게 되면 gradient가 0이 됌 -> 정보가 길어질 수록 gradient가 하나라도 0이 된다면 곱셈 연산이므로 누적된 정보가 0이 되어버림 => gradient vanishing / exploding problem
해결 방법
- LSTM(Long Short Term Memory)
- GRU(Gated Recurrent Units)
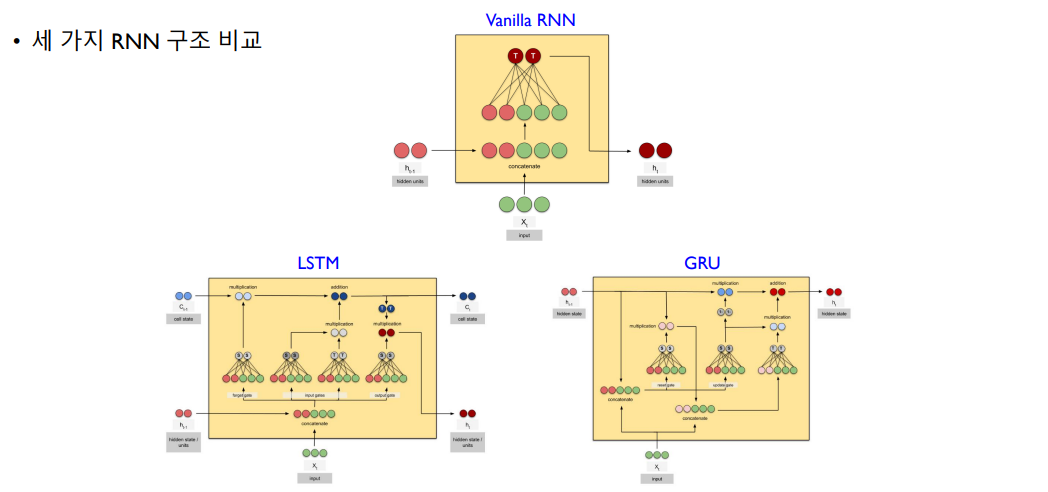
RNN Hidden Unit
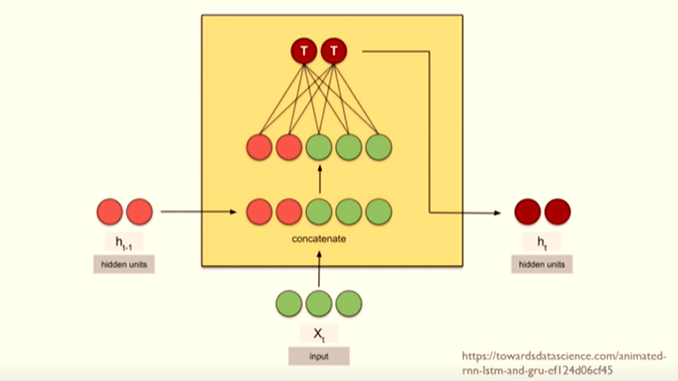
LSTM
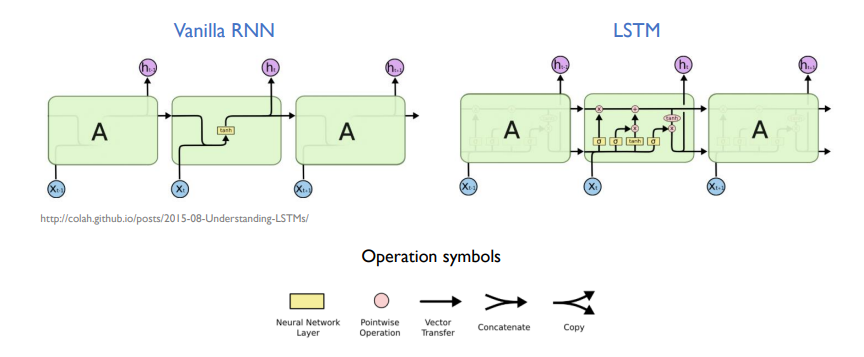
long term dependency 즉 장기의존성 학습이 가능함
Vanilla RNN
- input이 주어지고 이전 시점의 hidden state가 주어짐
- 초록색(input)과 빨간색(이전 시점 hidden state)을 concatenation
- concatenation 한 것이 neural network 연산 후에 output
- 다음 state로 내보냄
LSTM은 주기억장치와 보조기억장치가 같이 있어서, 보조기억장치를 통해 과거의 정보를 보존하고 선택적으로 반영
Cell state
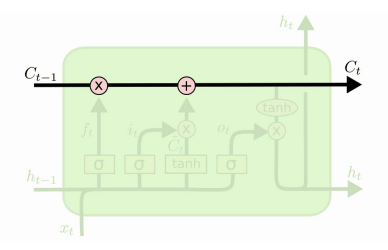
Step 1
Cell state 즉 보조기억장치에서 저장된 정보 중, 얼마만큼을 망각할지 결정 => forget gate
즉 과거의 정보가 현재 시점에서 얼마나 유용한가
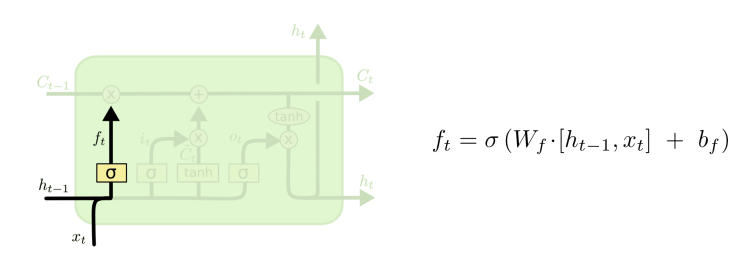
이전 단계 ht-1와 현 단계 입력 xt로부터 0,1 값을 출력함
- 0 : 지금까지 cell state에 저장된 모든 정보 무시
- 1 : 지금까지 cell state에 저장된 모든 정보 보존
Step 2
새로운 정보를 얼마만큼 cell state에 저장할지 결정 => Input gate
현재 시점에서 어떤 값을 update할지 결정
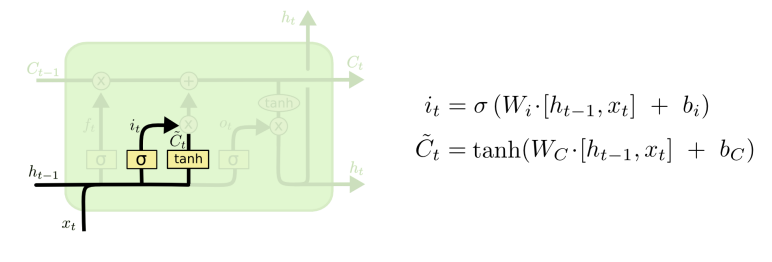
이전 단계 ht-1와 현 단계 입력 xt를 concat한 이후 W 가중치를 곱함
값이 클 수록 현재 시점에서의 정보를 최대한 많이 반영함
새로운 cell state에 저장될 정보의 후보를 결정함 => Tanh layer
Step 3
예전의 cell state를 새로운 cell state로 update함
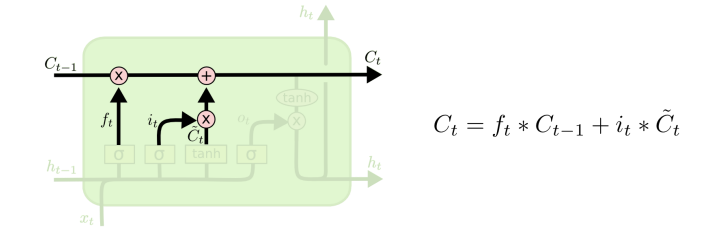
Ct-1 이전 시점의 정보를, ft 앞선 forget gate에서 학습한 값을 통해 얼마만큼 반영할 것인가
C^t 새로운 cell state 후보를, it 현재 시점에서 얼마만큼 반영해 줄 것인가
=> 이를 통해 새로운 Ct를 만들어냄
과거 정보를 얼마만큼 보존하고, 현재 정보를 얼만큼 반영할지 학습을 통해 adaptive하게 결정하겠다 !
Step 4
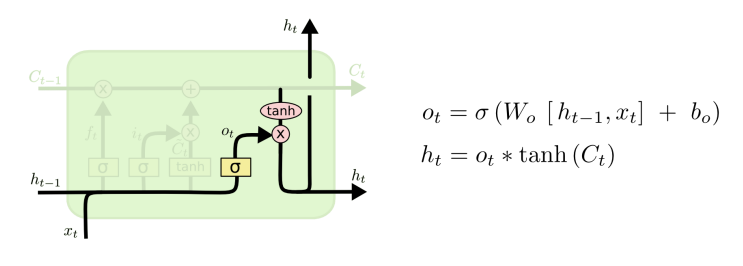
이전 단계 ht-1와 현 단계 입력 xt를 통해 => output gate(주기억)
output gate 값을 통해 현재 cell state 값을 update하고 최종적으로 ht를 산출함
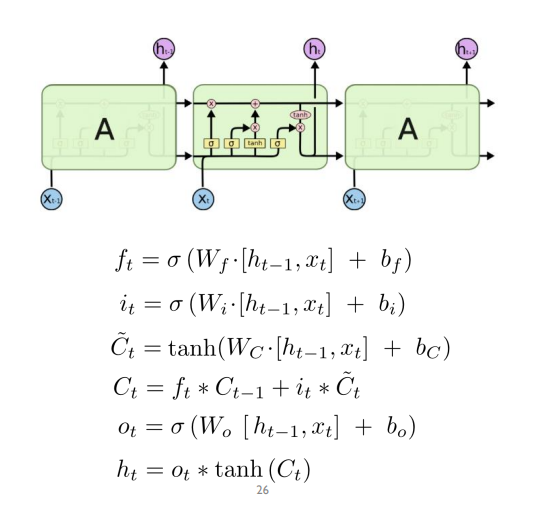
4가지의 가중치 행렬을 학습시켜야함
모든 상황의 입력은 ht-1과 xt를 concat해서 사용함
GRU
LSTM을 단순화 시킴
성능 차이가 크지 않음
forget gate와 input gate를 update gate로 결합함
reset gate를 통해 망각과 업데이트 정도를 결정
즉 update gate와 reset gate 2개를 사용하는 것
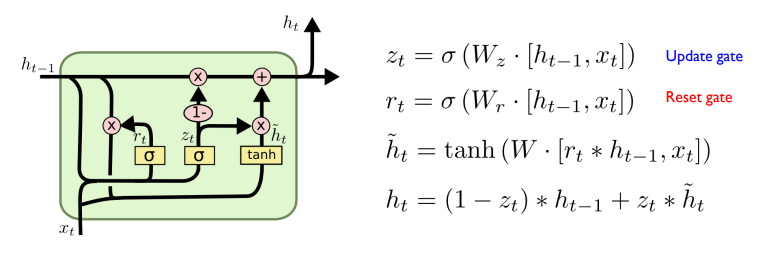
RNN Variations
Bidirectional RNN
데이터 정보 처리를 시간의 역방향으로 처리를 했을 때 성능이 좋아짐
따라서, 시간의 순방향과 역방향으로 정보를 처리하자
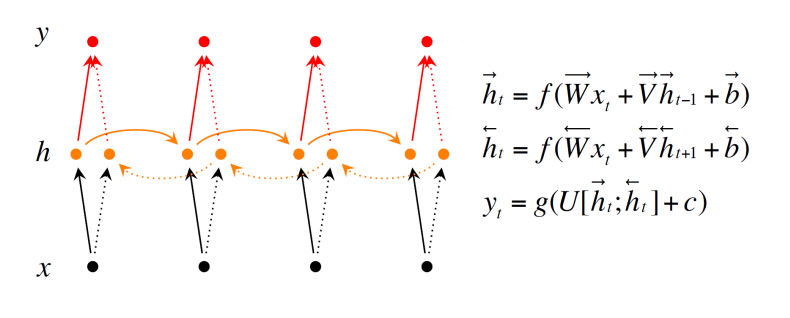
실선 : 순방향
점선 : 역방향
output : 순방향의 hidden vector와 역방향의 hidden vector를 concat해서 사용
Deep Bidirectional RNN
hidden layer를 여러 층으로 쌓음
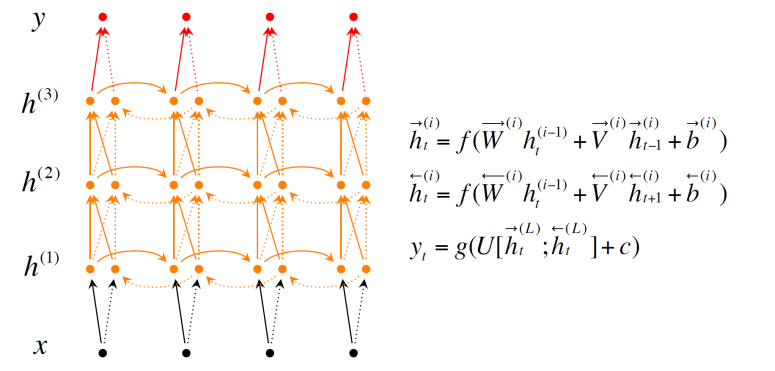
단 RNN은 층을 깊게 쌓는다고 성능을 보장하진 않음
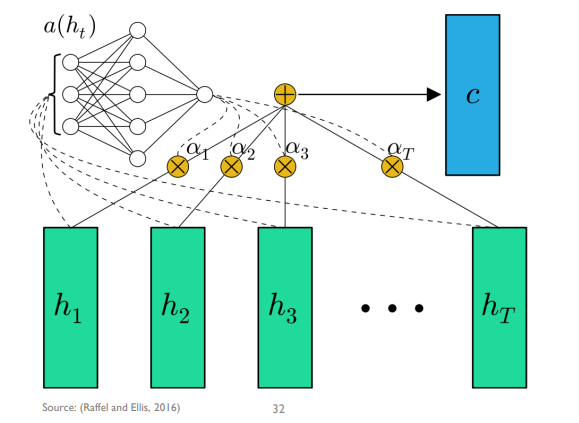
Attention
어느 시점의 정보가 RNN의 최종 출력 값이 영향을 미치는지 알려줄 수 있는 매커니즘
- Bahadanau attention
attention 모델을 위해 model 학습이 한번 더 필요 - Luong attention
별도 학습이 필요하지 않음
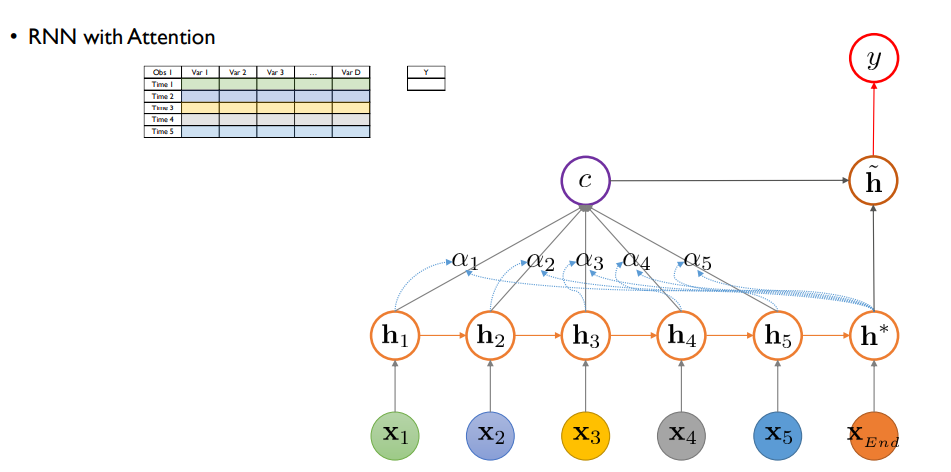
STEP 1.
각 시점별로 hidden state로 정보가 전달됌
attention 구조가 없었다면 h* 에서 바로 y를 예측하게 되지만
STEP 2.
attention이 있다면 가장 마지막 hidden state h* 와 각 hidden state 사이 유사도/기여도(알파)를 산출함

알파 : i번째 hidden state vector가 context vector 생성에 기여하는 비중, 해당하는 시점이 얼마나 최종 의사결정에 영향을 많이 미쳤는지의 기여도
기여도 : h* 제일 마지막 hidden state vector와 i번째 hidden state vector 사이의 함수 관계임. 이 함수가 알파가 0~1 사이 값으로 만들기 위한 softmax function에다가 안에 있는 score라는 함수를 적용하게 됌. score 함수는 두 hidden vector 사이의 단순 내적 사용해도 효과 있음. 즉 두 hidden vector가 유사할 수록 큰 값을 줌.
STEP 3.
알파들과 hidden state들의 선형 결합을 통해 c 라는 context vector를 만듬

기존 rnn, lstm, gru에선 중간 시점 hidden state 정보는 사용하지 않음. 가장 마지막 hidden state만 사용
attention을 활용하면 중간 시점의 hidden state 정보를 최종 의사결정에 활용하는 것
STEP 4.
context vector와 마지막 시점의 hidden state를 결합해서 새 hidden state vector를 만듬

concat한 vector에 W 가중치를 곱하고 비선형 활성화를 통해 만듬
STEP 5.
새 hidden state vector를 통해 y를 예측

attention 구조 장점
1. 성능이 훨씬 향상
2. 알파 값이 결국 0~1 사이 값이며 모든 알파 값을 합치면 1이 됌 => 즉 예측에서 몇 번째 시점이 가장 중요한 역할을 했는지를 알 수 있음
Summary