Threshold

먕먕·2022년 5월 20일

file:///C:/Users/Lee/Desktop/Recurrent_neural_networks_for_remaining_useful_life_estimation.pdf

1. Introduction

주된 알고리즘은 custom recurrent neural network architecture이다.
데이터를 필터링해 노이즈를 최소화하는 동시에 RUL을 추정할 수 있다.

2. Data Overview

training set은 218개의 다른 unit을 포함하며, failure까지 다 다른 길이의 cycled을 run한다. 최소는 127 cycle, 최대 356 cycle이다.
데이터의 특성들을 고려했을때 성능 저하와 관련이 있을 수 있는 데이터 추세를 발견하는 것은 쉽지 않음을 알 수 있다.
이러한 속성(직접적으로 이해하는 것이 어려운)은 머신러닝을 이 문제에 훌륭한 후보자로 만든다.

3. Classifier training

Multi-Layer Perceptron(MLP) Neural Network가 잘 작동할 수 있을까? 이러한 분류 작업을 성취하기 위해 MLP가 얼마나 커야할까? 훈련은 얼마나 길게 지속해야할까?
--> difficult/hard to solve
따라서 고급 데이터 전처리 기술이 필요하다.
데이터를 두 개의 세트로 나눈다고 가정하자. 하나는 healthy unit 나머지 하나는 degraded unit.
MLP는 degraded와 healthy unit을 구분하기 위해 학습하도록 사용된다. 이때 Extended Kalman Filter Training 방법을 사용하는데 이는 복잡한 모델을 학습할 수 있도록 도와준다. 분류 학습은 이 분류 작업이 MLP에 의해 쉽게 해결됨을 보여준다. 3층 구조 network는 빠르게 학습하며 compact하고 정확한 모델을 보여준다.
~한 환경에서 99.1%의 정확도를 보여줬다.
즉 raw input도 EKF와 MLP 네트워크가 healthy/degraded unit을 구분하는데 충분한 정보를 준다.

4. Approach for RUL learning

classifier 결과는 유용하고 흥미로웠지만 이 분류기는 RUL을 제공하지는 않는다. 따라서 RUL 추정을 위해 continuous variable representing the number of cycles remaining until failure(우리 코드에선 RUL - current cycle)가 필요하다
인공 시그널은 sequence가 끝나기까지 남은 cycle로 set된다. 기계 작동의 끝은 failure 전의 마지막 cycle이란 것을 고려한다면 sequence의 끝 전에 남은 샘플의 갯수가 정확한 RUL 값일 것이다.

5. MLP Function Estimator

MLP function estimator를 종료까지 남은 사이클 수로 학습시킨다. 그 전에 2개의 hidden layer을 가진 MLP를 EKF 훈련 알고리즘으로 훈련시킨다.

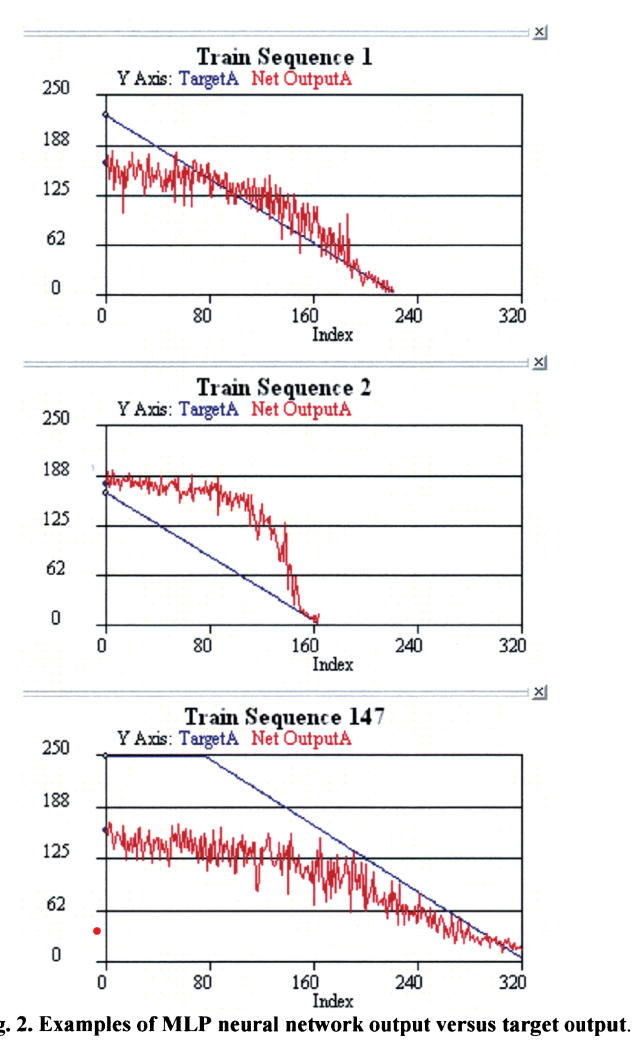
결과가 좀 흥미롭다. 우선 MLP network는 number of remaining cycles를 대략적으로 학습하는 것이 가능하다는 것을 알 수 있다. 그리고 output 곡선이 비교적 평탄하게 시작한 이후 end of run 근처에서 0까지 감소한다.
각 그림은 일관된 특징이 있다. sequence의 약 1/3까지는 MLP 결과가 상당히 평평하고 마지막 1/3은 MLP 결과가 선형적으로 0까지 감소한다. 가운데 1/3 부분에서는 꺾이는 무릎 부분이 나타나는데 여기가 failure first develop 하는 부분이다.
MLP 결과에는 센서 노이즈로 인한 노이즈도 많다. 정확도를 위해 이것은 제거되어야 한다.
후반부의 곡선 기울기는 다 다르다.
데이터에 대한 최종 관측의 초기 결과는 sequence마다 조금씩 다르다
MLP는 초기 제조 용인(?)과 초기 마모를 찾아낸 것으로 보인다.
훈련된 network 결과의 특징 분석은 target output에 변화를 유발했는데, 최대 target 결과값이 모든 sequence에서 상수 값으로 제한되었다는 것이다. 성능 저하는 unit이 어느 기간 정도 작동하고 초기 고장이 발생해야 알아차릴 수 있기에 기계의 성능이 저하되기 전에 RUL을 추정하는 것은 비합리적일 수도 있다.
기계가 새로운 상태이고 매우 건강한 상태일 때 얼마나 오래 지속될지 어떻게 예상할 수 있는가? 장치가 일정 시간 동안 작동한 후에야 저하가 나타나고 RUL의 상대적인 표시를 제공한다. 이러한 이유로 시스템이 새로운 경우 RUL을 상수 값으로 추정하는 것이 타당해 보인다.
초기 상수 RUL 값을 선택하기 위해 다음과 같은 추정이 사용되었다

최소 run length는 127이다.

평균 run length는 209이다. 곡선의 꺾이는 부분은 105번 근처에서 발생해야 한다.

MLP 결과는 140과 180 사이에서 평균 steady(고정적인) 상태 출력을 보여준다.

negative RUL 추정 오류는 positive 오류보다 적게 페널티를 받는다.

이 추정들에 근거하여 초기 RUL은 120~130 cycle로 정했다. 최대 RUL이 다른 경우들에 대해 추가적 실험이 있었고(웹사이트에 올렸다고 함;;), 어떠한 limit이 가장 잘 작동했는지 평가했다. 최종 결과는 130이다.

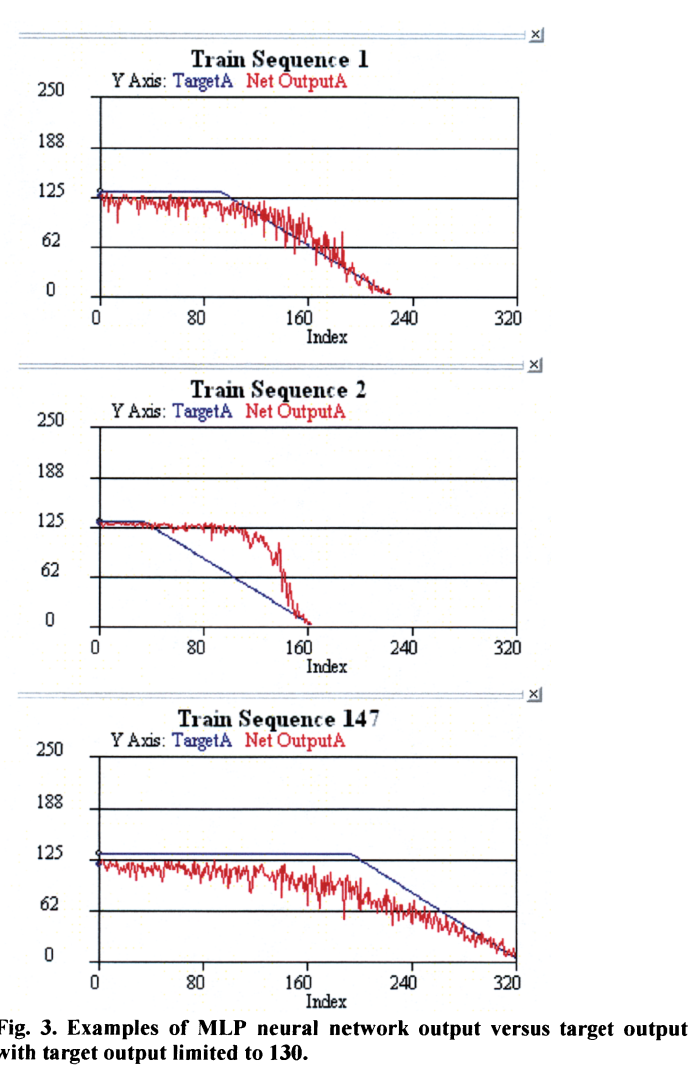
RUL limit 130을 사용한 결과에서 몇 관측이 있었다.

output에 노이즈가 좀 감소한 느낌이다.

This is much less than the prior initial steady state output as one would expect since the initial values of the training output are now much smaller.

곡선의 꺾이는 부분이 크게 변하지 않았고 기울기도 전과 유사하다

이 결과들은 기계가 failure에 가까워질때 MLP가 상당히 정확하게 RUL을 예측한다는 것을 알려준다. 초기, 중반부에서 RUL을 예측하는 것은 더 어렵고 성능도 좋지 않다.

MLP neural network가 이 문제에 적합하지 않은 이유는 다음과 같다.

데이터 셋은 temporal sequence이며 input/output 매핑에 시간 종속성이 있따. MLP는 현재 상태만 고려하는 정적 매핑을 한다.

input 데이터는 노이즈가 많다. noise가 많은 input 데이터는 결과에 상당한 노이즈를 발생시킨다.

time domain filtering을 모델링 과정에 통합시키는 것이 개선된 솔루션에 대한 다음 단계이다.

6. Filtering Approach (Recurrent Neural Network)

데이터 필터링은 양이 많고 노이즈가 많으며 시간적 특징을 가진 데이터에서 정확한 RUL을 추출하기 위해 중요해 보인다. 선형/비선형 시간 domain 필터를 MLP 결과에 적용시킬 수도 있지만, 이런 필터의 해석적 도출은 쉽지 않다. 따라서 모델에 필터링을 통합한 신경망 훈련이 더 나은 방법일 것이다. 신경망 훈련 알고리즘은 원하는 결과 신호와 일치하도록 자동으로 최적에 가까운 필터를 도출한다.
시간 domain 모델링이나 필터링에 자주 사용되는 직접적인 접근법은 신경망을 각 입력 파라미터들의 multiple time delayed examples로 표현하는 것이다. 이것은 표준 정적 신경망과 정적 파생 계산이 사용되기 때문에 구현하기 직관적이고 쉽지만 문제가 많다. input으로 얼마나 많은 예가 필요한지 모르고 시간을 얼마나 거슬러 올라가야하는지 알기 어렵다. 한정된 수의 과거 상태만 고려될 수 있다. 많은 시도와 오류 수정이 필요하다. 또 다른 문제는, network가 2,3배 많은 input을 갖고 있다는 것이다. 더 커지고 weights들은 더 많은 계산을 요구한다. 또한 weight가 많아져 overfitting 위험성이 커진다. overfitting을 해결하기 위해 SVM(support vector machine)과 같은 복잡한 모델링 접근이 필요하다. 그러나 SVM은 10~100배 큰 모델이다.
비선형 시간 동적 시스템을 다루기 위한 더 나은 방법은 RNN을 사용하는 것이다. RNN은 내부 메모리와 피드백을 활용하고 복잡한 비선형 동적 매핑을 통해 학습한다. 또한 이전 입력과 hidden state의 임의의 수를 설명할 수 있으며 hidden layer를 강력하게 학습한다.
advanced proprietary recurrent neural network 구조와 학습 알고리즘은 항공기 비행 역학, 터빈 엔진 역학 및 기타 복잡한 비선형 동적 시스템 모델링과 같은 문제를 위해 개발되었다.
RNN에서 어려운 것은 네트워크 가중치의 gradient를 계산하는 것이다. gradient는 출력 오류 함수로 계산되어야 할 뿐 아니라 시간적 변동을 고려하여 시간적 역순으로 계산되어야 한다. 우리 RNN은 graident를 계산하기 위해서 bruncated back propagation through time(BPTT)을 사용한다.
RNN도 EKF를 사용해서 네트워크 가중치를 업테이트 한다. EKF는 훈련 반복 횟수를 최소화하고 매 훈련 반복에 모든 훈련 데이터를 사용할 필요가 없기 때문에 recurrent network에 효과적이다. RNN의 마지막 특징은 신경망 모델을 최적화해 수행하는 반복적 과정을 자동화하기 위해 진화 알고리즘을 통합한다는 것이다. 이것은 인간의 노력의 양을 매우 줄여주고 정확한 모델을 생산한다. 진화 알고리즘은 다수의 솔루션을 유지하고 조정하여 솔루션을 개선한다. 우린 RNN의 구조, 각 layer의 hidden node, 몇개의 다른 variable, EKF 훈련을 위한 두개의 상수 (R,Q)를 구현한다. 또한 traing data set과 독립적인 validation data set을 사용한다.
train data에 촘촘하게 맞추는 것이 최선의 솔루션은 아니다. overfitting 위험이 있고 다른 데이터에 잘 일반화하지 못하기 때문이다. 따라서 Differential Evolution(DE)는 training accuracy가 아닌 validation data set으로만 순위를 매긴다. 훈련 데이터와 무관하게 높은 정확도를 생성하는 network가 더 나은 모델이 될 것이며 overfitting 가능성도 적다.

7. Differential Evolution

DE는 실제 가치 다중 모델 함수를 최적화하는 효율적인 방법이며 개념적으로 단순하고 사용하기 쉬운 것으로 나타났다.
DE는 솔루션이 실제 값 매개 변수의 벡터로 코딩되는 병렬 방향 검색 방법이다.
처음에는 모집단이 전체 검색 공간을 차지하며 벡터 간의 차이가 클 것이다.
따라서 진화 과정 초기에 알고리즘은 검색 과정에서 더 큰 단계를 변경하고 전체 공간을 적극적으로 검색할 것이다.
모집단이 수렴함에 따라 차이 벡터는 작아지고 알고리듬은 검색 공간의 최소값으로 수렴하기 위해 자동으로 더 작은 단계 변화를 활용한다.
훈련 과정은 수백 개의 네트워크를 훈련시키고 좋은 해결책으로 수렴할 것이다.
이를 통해 엔지니어가 솔루션을 찾기 위해 거쳐야 하는 일반적인 시행착오 실험 프로세스가 제거되고 시스템 모델링에 소요되는 시간과 비용이 절감된다.

8.Recurrent Neural Network Output

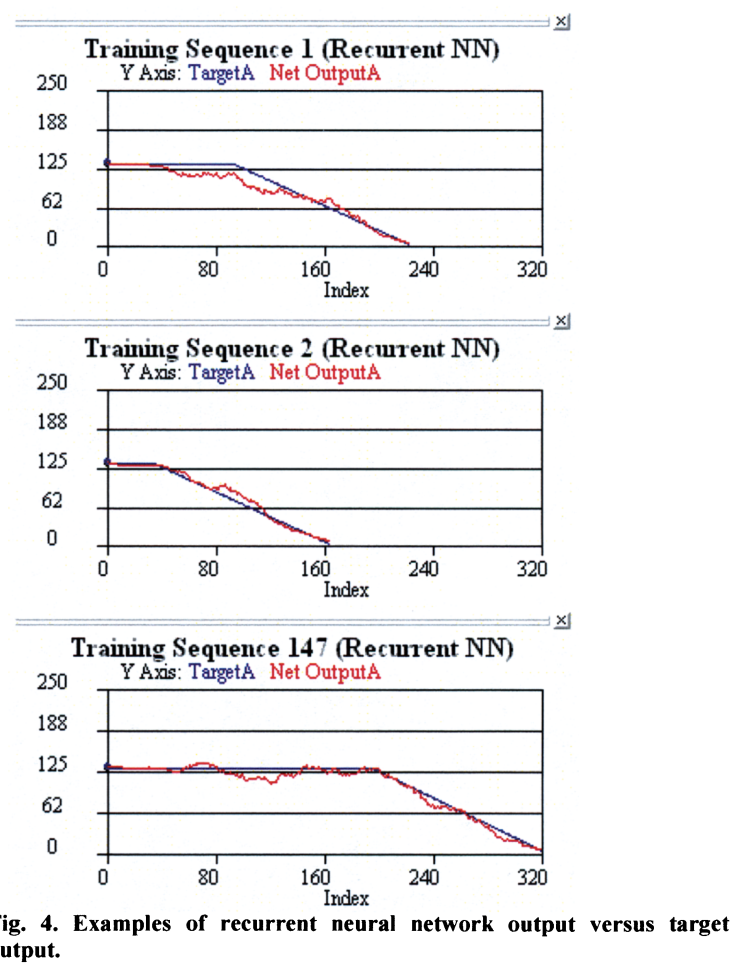
반복 신경망은 정적 MLP보다 훨씬 정확하게 원하는 훈련 데이터와 일치했다.
반복 신경망은 MLP가 제공할 수 없는 시간 영역 필터링을 제공할 수 있기 때문에 네트워크의 출력은 MLP 네트워크보다 소음이 훨씬 적다. 또한 각 시퀀스가 끝날 무렵에 반복되는 신경망 출력이 훨씬 더 선형적이고 일관적이라는 점도 흥미롭다. 각 시퀀스에 대해 반복 신경망 출력은 0에 가까워짐에 따라 선형적으로 감소하며 각 시퀀스에 대해 붕괴 속도는 일정하다.
반복 신경망은 시스템이 언제 고장나기 시작하는지 감지할 수 있고 과거 상태 정보의 피드백을 제공함으로써 고장에 대한 일관된 응답을 학습할 수 있다.
네트워크가 정확히 어떻게 이것을 할 수 있는지는 물론 알려져 있지 않지만, 그것이 기계 학습 접근법의 이점이다. 인간 개발자는 문제의 모든 기본 물리학을 이해할 필요가 없기 때문에 훨씬 더 빨리 해결책을 개발할 수 있다.