재귀 (Recursion)
재귀 호출
- 재귀 호출 (Recursive call)
: 호출되는 메소드가 호출하는 메소드와 동일한 메소드 호출
- 재귀의 종류
- Direct recursion
: 메소드가 자신을 직접 호출하는 재귀 - Indirect recursion
: 두 개 이상의 메서드 호출 체인이, 체인을 시작한 메서드로 반환되는 재귀
- Direct recursion
- 관련 용어
- Base case
- 해가 비재귀적으로 서술될 수 있는 특수한 경우
(답이 알려진 경우) - 하나의 재귀에 복수의 base case가 존재할 수 있다.
- 해가 비재귀적으로 서술될 수 있는 특수한 경우
- General (recursive) case
- 해결책이 자신의 더 작은 버전으로 표현되는 일반적인 경우
- 문제가 해결될 때까지 계속 반복됨 (무한루프 주의)
- Base case
- 재귀적 알고리즘
: 해결책이 자기 자신의 더 작은 인스턴스인 general case와, base case로 표현되는 알고리즘✏️ 재귀적 알고리즘의 조건
- 각각 적어도 하나 이상의 base case와 general case를 가져야 한다.
- 재귀 함수가 연속적으로 호출될수록 답이 알려진 상황(base case)에 가까워져야 한다.
→ base case에 도달할 경우 재귀 종료if (some condition for which answer is known) solution statement // base case else recursive function call // general case
재귀(recursion)과 반복(iteration)의 비교
✏️ 프로그래밍 언어가 자체적으로 지원하지 않는 경우를 제외하고, 모든 재귀와 반복은 서로 대체 가능하다.
단, 효율성에 차이가 있으며 꼬리 재귀가 아닌 경우 반복으로 치환하기 위해서는 stack 등의 특수한 구조를 사용해야 한다.
- 재귀
- if문 이용 (branching structure)
- 재귀를 사용하기에 좋은 경우
- shallow depth
: 재귀 호출의 깊이가 문제의 크기에 비해 상대적으로 얕을 때 - effeciency
: 재귀 버전과 비재귀 버전이 거의 동일한 양의 작업을 수행할 때 - clarity
: 재귀 버전의 솔루션이 비재귀 버전보다 짧고 간단할 때
(예: 포인터 변수가 사용될 때)
- shallow depth
- 재귀를 사용하기에 좋지 않은 예시
- 중복 계산을 여러번 수행할 때
- 문제의 크기가 상수만큼씩 줄어들을 때
(예: combination)
- 반복
- 루트 이용 (looping structure)
- 재귀의 장단점
- 장점
- 재귀로 구현한 코드는 일반적으로 더 짧고 이해하기 쉽다.
- 단점
- 일반적으로 반복보다 시간 및 공간 측면에서 비효율적
(→ 재귀를 사용할 땐 주의해야 한다.)
- 일반적으로 반복보다 시간 및 공간 측면에서 비효율적
- 장점
재귀의 제거
✏️ Tail Recursion
- 함수에 포함된 단일 재귀 호출이 함수에서 실행되는 마지막 명령문인 경우
- 상대적으로 쉽게 재귀를 제거하고 반복으로 대체될 수 있다.
-
Tail Recursion인 경우
-
재귀가 호출될 때 활성화 레코드가 런타임 스택에 배치되고 함수의 매개변수와 지역 변수를 보유하게 되는데,
tail recursion인 경우 재귀 호출이 함수의 마지막 명령문이기 때문에 함수는 이러한 값들을 사용하지 않고 종료된다. -
따라서 재귀 호출의 매개변수 목록에서 "더 작은 호출자" 변수를 변경한 다음 함수의 시작 부분으로 다시 "점프"해야 한다.
즉, 루프가 필요하다! -
base cases
: become the terminating conditions of the loop -
general case
: each subsequent execution of the loop body processes a smaller version of the problem
- 예:
ValueInList- 재귀를 이용한 코드
//pre : list is implemented by static array bool ValueInList(ListType list, int value, int startIndex) { if (list.info[startIndex] == value) // base case 1 : 찾은 경우 return true; else if (startIndex == list.length - 1) // base case 2 : 찾지 못한 경우 return false; else // general case return ValueInList(list, value, startInex + 1); // 순차 검색 }- 재귀를 제거해 반복으로 치환한 코드
bool ValueInList(ListType list, int value, int startIndex) { bool found = false; while (!found && startIndex < list.length) // includes both base caes { if (value == list.info[startIndex]) found = true; else startIndex++; // related to the general case } return found; }
-
-
Tail Recursion이 아닌 경우
-
일반적으로 재귀 함수의 호출이 반환되기 전에 추가 작업을 수행한다.
→ 함수의 호출이 반환될 때까지 해당 호출의 상태를 유지하기 위해 스택에 정보를 저장하고, 호출이 완료된 후 이전의 상태로 복구해야 한다.
→ 시스템에 의해 자동으로 수행되는 stacking을 프로그래머가 수동으로 수행하는 stacking으로 대체해야 한다.
-
예:
RevPrint- 재귀를 이용한 코드
void RevPrint(NodeType* listPtr) { if (listPtr != NULL) // general case { RevPrint(listPtr->next); cout << listPtr->info << endl; } } // base case : if the list is empty, do nothing-
재귀를 제거해 반복으로 치환한 코드
#include "Stack.h" // 재귀의 활성화 레코드(스택)의 원리, 직접 구현 // The Stack allows to store pointers and retrieves them in reverse order void ListType::RevPrint() // member function { StackType<NodeType>* stack; NodeType* listPtr; listPtr = listData; while (listPtr != NULL) // 스택 순차적으로 방문하면서 스택에 포인터 push { stack.Push(listPtr); listPtr = listPtr->next; } while (!stack.IsEmpty()) // 스택의 원소 top부터 출력 -> 자동으로 역순 출력 { listPtr = stack.Top(); stack.Pop(); cout << listPtr->info; } }
-
재귀를 이용한 예제 코드
Factorial
- 코드
int Factorial(int number) { if (number == 0) // base case return 1; else // general case return number * Factorial(number-1); }
Combination
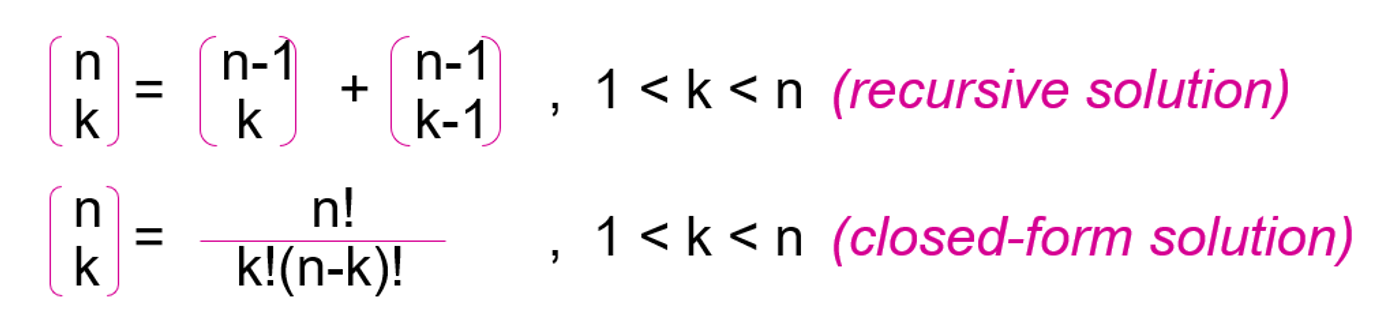
조합은 재귀 함수로 구현할 경우 굉장히 비효율적인 문제이다.
(중복된 연산을 여러 번 수행하기 때문에)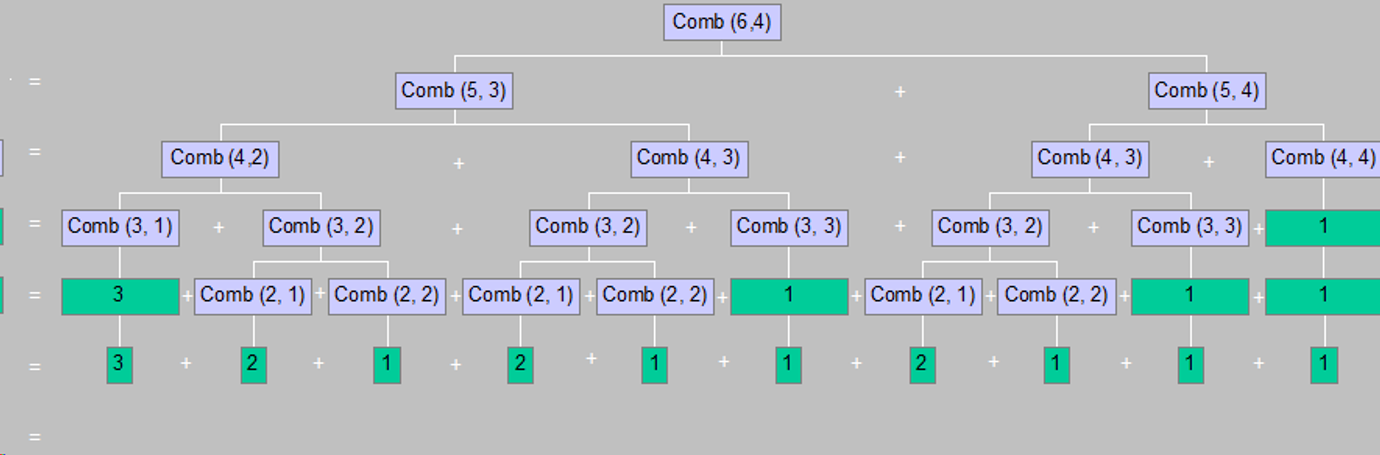
- 코드
- base case
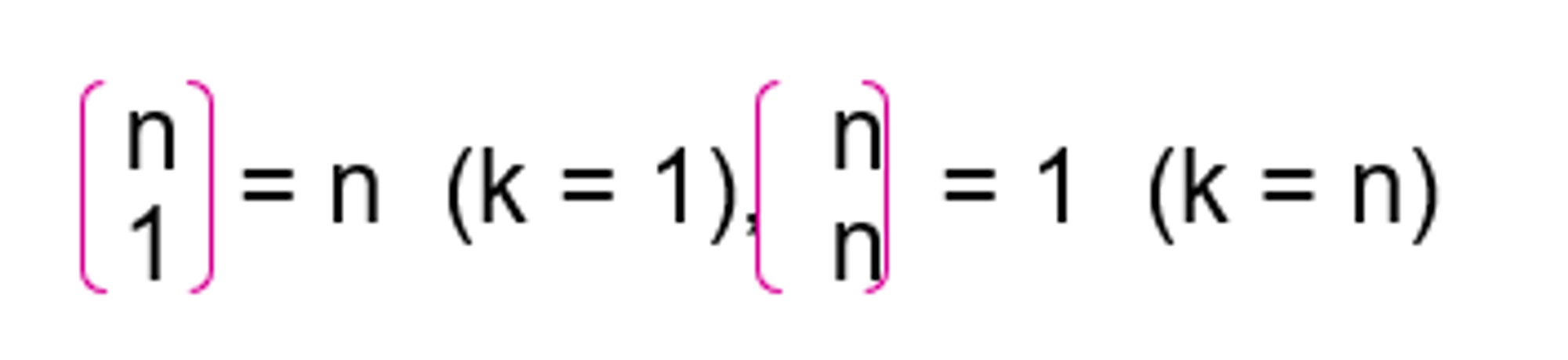
- general case
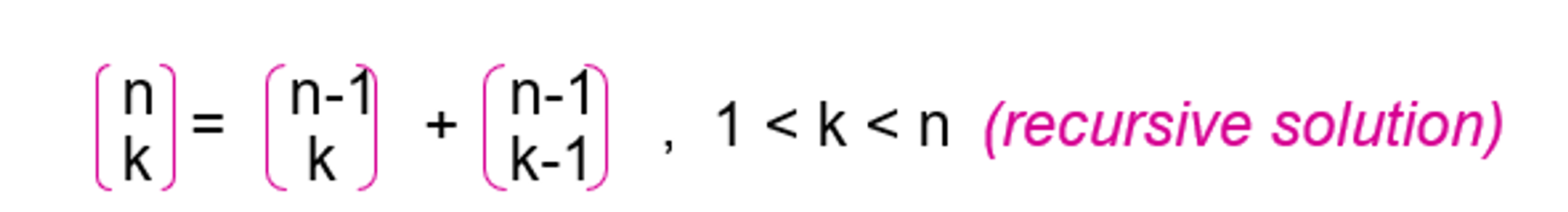
- base case
int Combinations(int n, int k)
{
if (k == 1) // base case 1
return n;
else if (n == k) // base case 2
return 1;
else // general case
return Combinations(n-1, k) + Combinations(n-1, k-1);
}Power (제곱)
- 코드
// pre: n >= 0 and x and n are not zero
int Power(int x, int n)
{
if (n == 0) // base case
return 1;
else // general case
return x * Power(x, n-1);
}List
- 구체적인 리스트의 구현 형태는 각 연산(함수)에 따라 다르다.
✏️ 동적 배열로 구현된 리스트의 코드
const int MAX_ITEMS = 100; // 최대 아이템 수 struct ListType { int length; int* info; // int 배열에 대한 포인터 } ListType list; // 생성자에서 리스트의 size 받아서 동적 할당하기 list.info = new int[size]; // 소멸자에서 동적 할당 해제하기 delete[] list.info;
- ValueInList
- 리스트 내의 아이템을 검색하는 함수
- list[startIndex] ~ list[length-1] 사이에서 검색
- 순차 검색 이용

- 코드
: 리스트가 정적 배열로 구현된 형태struct ListType { int length int info[MAX_ITEMS]; ListType list; }bool ValueInList(ListType list, int value, int startIndex) { if (list.info[startIndex] == value) // base case 1 : 찾은 경우 return true; else if (startIndex == list.length - 1) // base case 2 : 찾지 못한 경우 return false; else // general case return ValueInList(list, value, startInex + 1); // 순차 검색 }✏️ iteration으로 구현한
ValueInListbool ValueInList(ListType list, int value, int startIndex) { bool found = false; while (!found && startIndex < list.length) { if (value == list.info[startIndex]) found = true; else startIndex++; } return found; }
- 리스트 내의 아이템을 검색하는 함수
- RevPrint
- 연결 리스트의 요소들을 역순으로 출력하는 함수
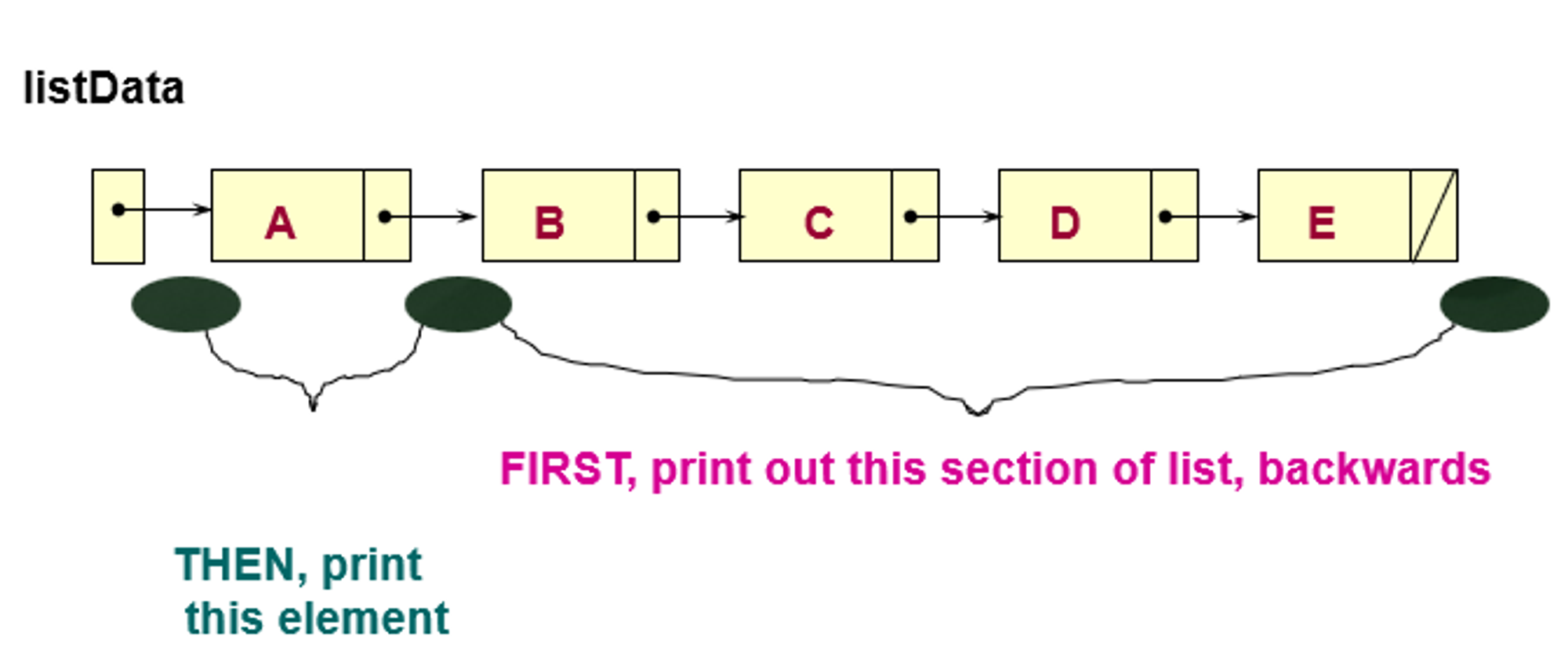
- 코드 (재귀)
void RevPrint(NodeType* listPtr) { if (listPtr != NULL) // general case { RevPrint(listPtr->next); cout << listPtr->info << endl; } // base case : if the list is empty, do nothing }✏️ iteration으로 구현한
RevPrint#include "Stack.h" // 재귀의 활성화 레코드(스택)의 원리, 직접 구현 void RevPrint() { StackType<NodeType>* stack; NodeType* listPtr; listPtr = listData; while (listPtr != NULL) // 스택 순차적으로 방문하면서 스택에 포인터 push { stack.Push(listPtr); listPtr = listPtr->next; } while (!stack.IsEmpty()) // 스택의 원소 top부터 출력 -> 자동으로 역순 출 { listPtr = stack.Top(); stack.Pop(); cout << listPtr->info; } }
- 연결 리스트의 요소들을 역순으로 출력하는 함수
- Binary Search
- 재귀 호출을 사용해서 정렬 리스트 내에 아이템이 있는지 검사
(이진 검색)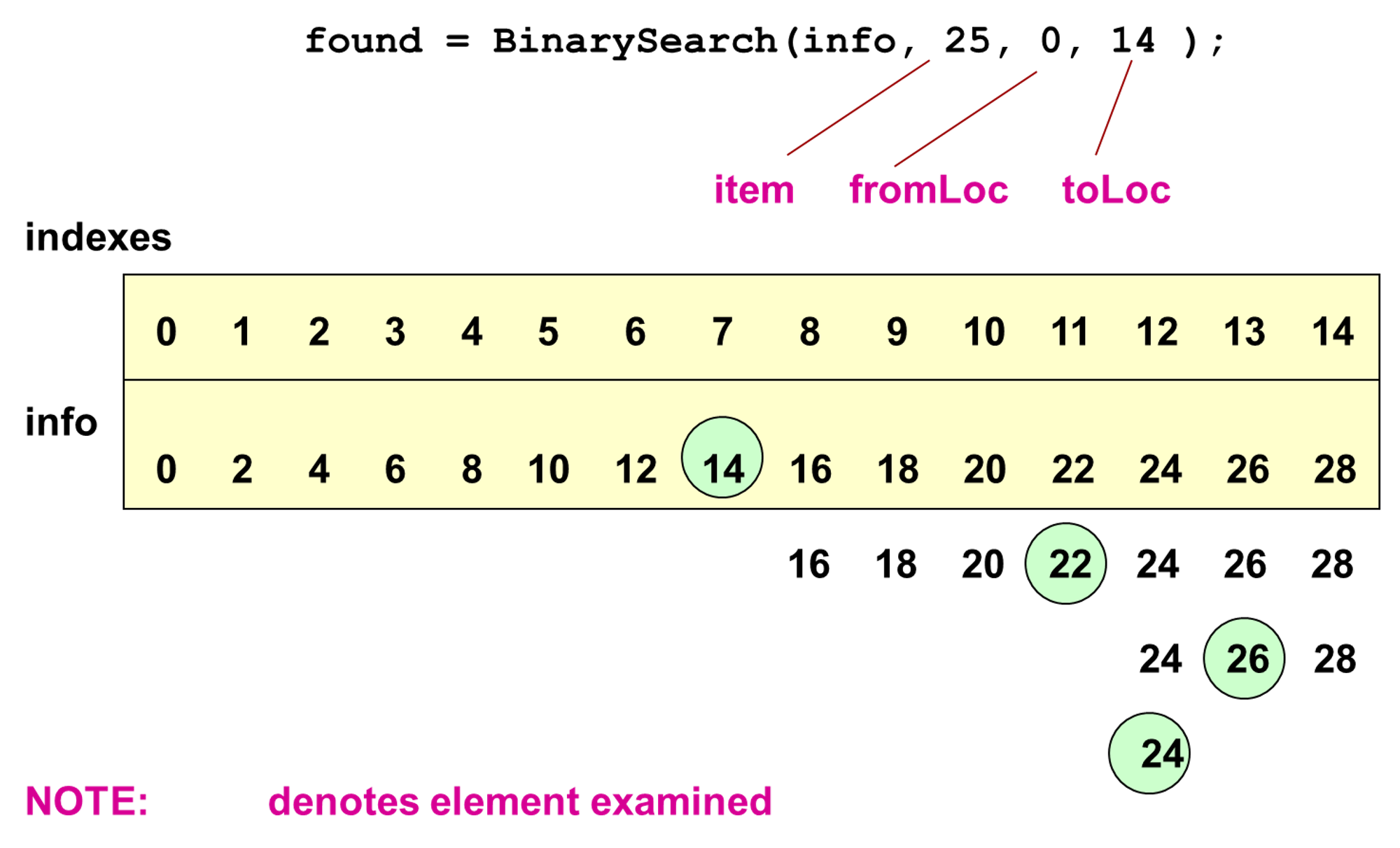
- 코드
template<class ItemType> bool BinarySearch(ItemType info[], ItemType item, int fromLoc, int toLoc) { int mid; if (fromLoc > toLoc) // Base case 1: 리스트 내에 아이템이 존재하지 않을 때 return false; else { mid = (fromLoc + toLoc) / 2; if (info[mid] == item) // base case 2: found at mid return true; else if (item < info[mid]) // general case 1 : search lower half return BinarySearch(info, item, fromLoc, mid-1); else // general case 2 : search upper half return BinarySearch(info, item, mid+1, toLoc); } }info[]: 검색할 리스트 (리스트가 배열로 구현된 형태)item: 검색할 아이템fromLoc: 검색을 시작할 인덱스toLoc: 검색을 끝낼 인덱스
✏️ iteration으로 구현한
RetrieveItemtemplate<class ItemType> bool SortedType<ItemType>::RetrieveItem(ItemType& item, bool& found) { int midPoint; int first = 0; int last = length - 1; while (first <= last) { midPoint = (first + last) / 2; if (item < info[midPoint]) last = midPoint - 1; else if (item > info[midPoint]) first = midPoint + 1; else { item = info[miPoint]; return true; } } return false; // 끝까지 못 찾은 경우 } - 재귀 호출을 사용해서 정렬 리스트 내에 아이템이 있는지 검사
Sorted Linked List
- 자료 구조
: 연결 리스트로 구현된 정렬 리스트
strcut NodeType
{
int info;
NodeType* next;
}
template <class ItemType>
class SorteydType
{
public:
void InsertItem(ItemType)
void DeleteItem(ItemType)
private:
NodeType* listData;
}- InsertItem
- 정렬 리스트(연결 리스트로 구현)에 어떤 아이템을 추가하는 함수
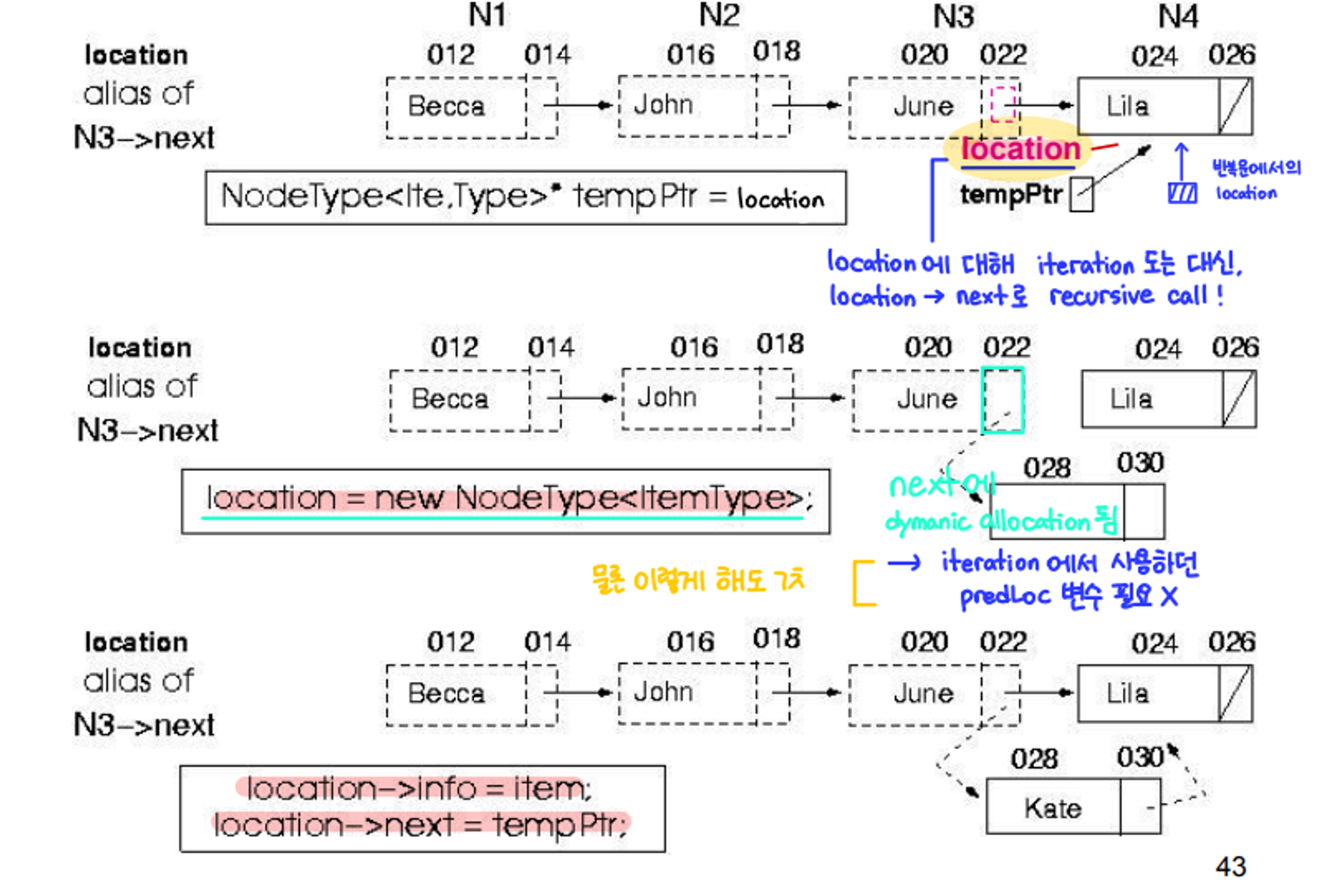
- 코드
// 정의 template<class ItemType> void Insert(NodeType<ItemType>* &location, ItemType item) { if ((location == NULL) || (item < location->info)) // base case 1 : 빈 리스트인 경우 // base case 2 : 아이템을 추가할 위치를 찾은 경우 { // 해당 위치(location)에 새로운 아이템 삽입 NodeType<ItemType>* tempPtr = location; location = new NodeType<ItemType>; location->info = item; location->next = tempPtr; } else // general case Insert(location->next, newItem); } // 호출 // : wrapper 함수에서 시작점(listData) 설정하고 호출 template<class ItemType> void SortedType<ItemType>::InsertItem(ItemType newItem) { Insert(listData, newItem); }
- 정렬 리스트(연결 리스트로 구현)에 어떤 아이템을 추가하는 함수
- DeleteItem (Sorted List)
- 정렬 리스트(연결 리스트) 내에 존재하는 어떤 아이템을 삭제하는 함수
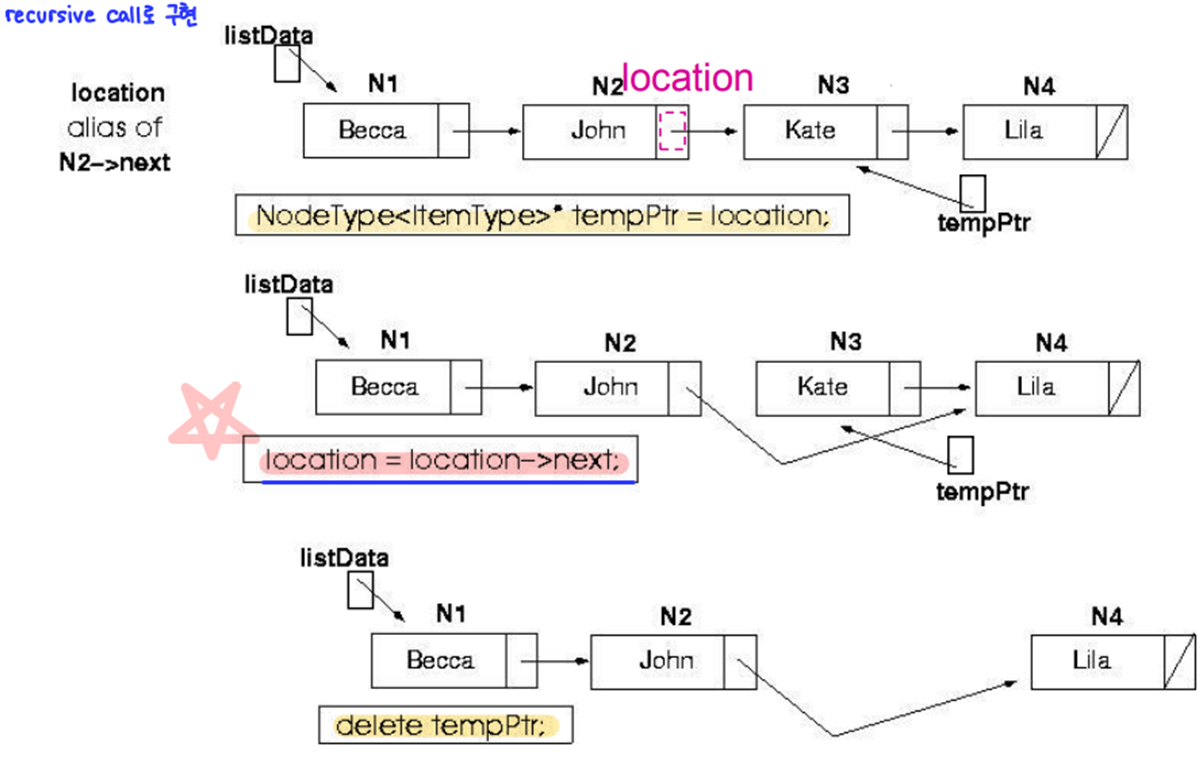
- 코드
// 정의 template<class ItemType> void Delete(NodeType<ItemType>* &location, ItemType item) { if (item == location->info) // base case : 삭제할 아이템을 찾은 경우 { NodeType<ItemType>* tempPtr = location; location = location->next; delete tempPtr; } else // general case Delete(location->next, item); } } // 호출 template<class ItemType> void SortedType::DeleteItem(ItemType item) { Delete(listData, item); }
- 정렬 리스트(연결 리스트) 내에 존재하는 어떤 아이템을 삭제하는 함수
Quick Sort
- Split

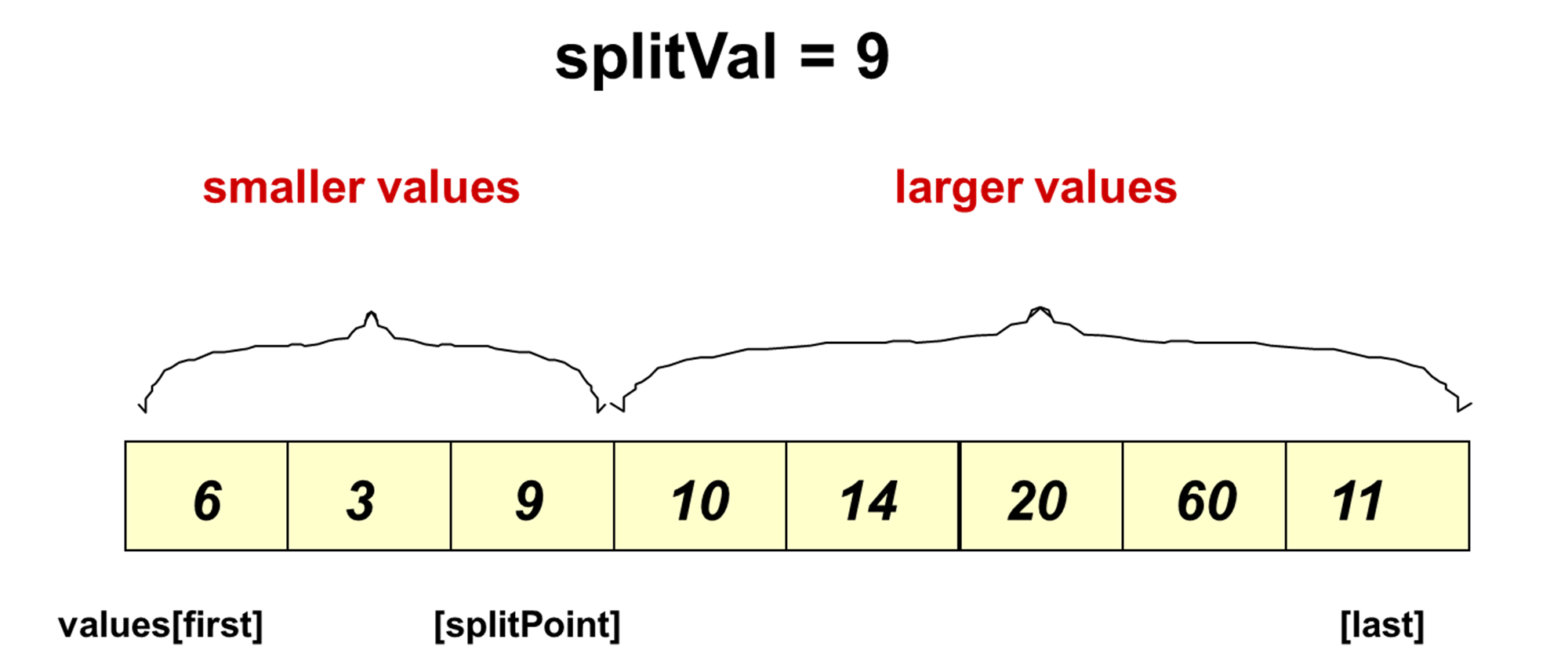
template<class ItemType>
void Split(ItemType values[], int first, int last, int& splitPoint)
{
ItemType splitVal = values[first];
int left = first + 1;
int right = last;
while (left <= right) { // 수정: left가 right를 넘어가지 않도록 변경
while (left <= last && values[left] < splitVal) {
left++;
}
while (right > first && !(values[right] < splitVal)) {
right--;
}
if (left < right)
Swap(values[left], values[right]);
else
break;
}
Swap(values[first], values[right]);
splitPoint = right;
}- QuickSort
template<class ItemType>
void QuickSort(ItemType values[], int first, int last)
{
if (first < last)
{
int splitPoint; // quick sort를 수행할 기준 index
QuickSort(values, first, splitPoint-1); // splitValue보다 작은 값을 가진 그룹에 대해 재귀 호출
QuickSort(values, splitPoint+1, last); // splitValue보다 큰 값을 가진 그룹에 대해 재귀 호출
}
}함수가 호출될 때 발생하는 일
Function Call
- 단계
- 제어권, calling block에서 함수 코드로 이동
- 함수 코드 실행
- 호출 블록의 특정 위치(return address)로 복귀
- 함수가 호출될 때 런타임 스택이 사용된다. 이 스택에는 함수 호출에 대한 Activation record (Stack frame)이 배치된다.
함수의 정보 (지역 변수, 매개변수)는 메인 메모리의 스택 영역에 할당되는데, 이때 스택(자료구조)의 원리를 사용해서 메모리의 할당과 해제를 관리한다.

Stack Activation Frame
- Activation Record
- 활성화 레코드에 저장되는 데이터
- 함수 호출에 대한 반환 주소 (return address)
- 함수의 매개 변수, 로컬 변수
- 함수의 반환값 (void가 아닌 경우)
: 함수의 반환값은 호출 블록의 반환 주소에서 사용하기 위해 반환 주소로 복귀한다.
- 특정 함수 호출에 대한 활성화 레코드는 함수 코드의 최종 닫힘 괄호
}에 도달하거나, 함수 코드의 반환문에 도달할 때 런타임 스택에서 pop 된다.
- 활성화 레코드에 저장되는 데이터
- 예시
- 코드

- 런타임 스택 활성화 레코드
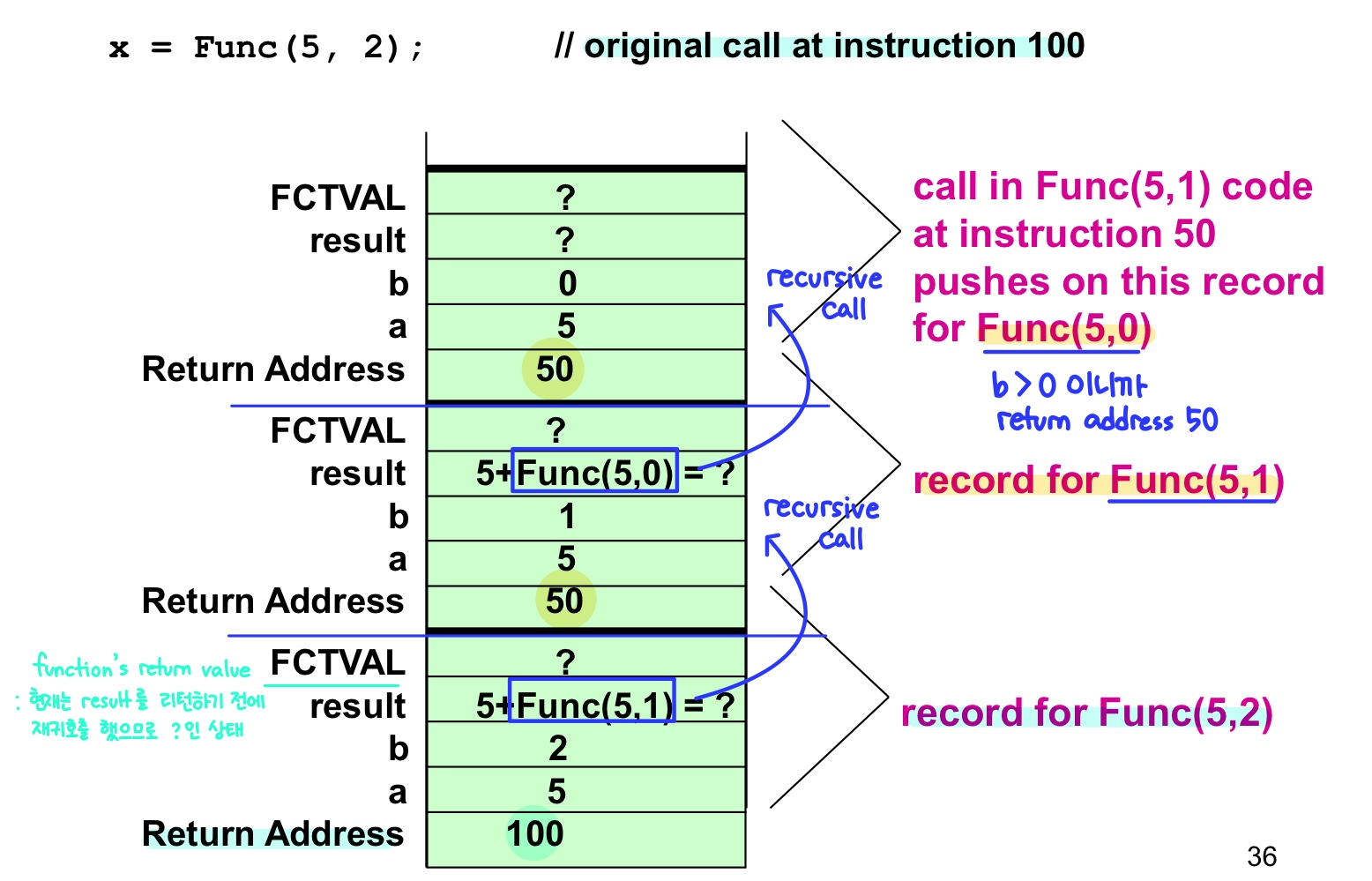
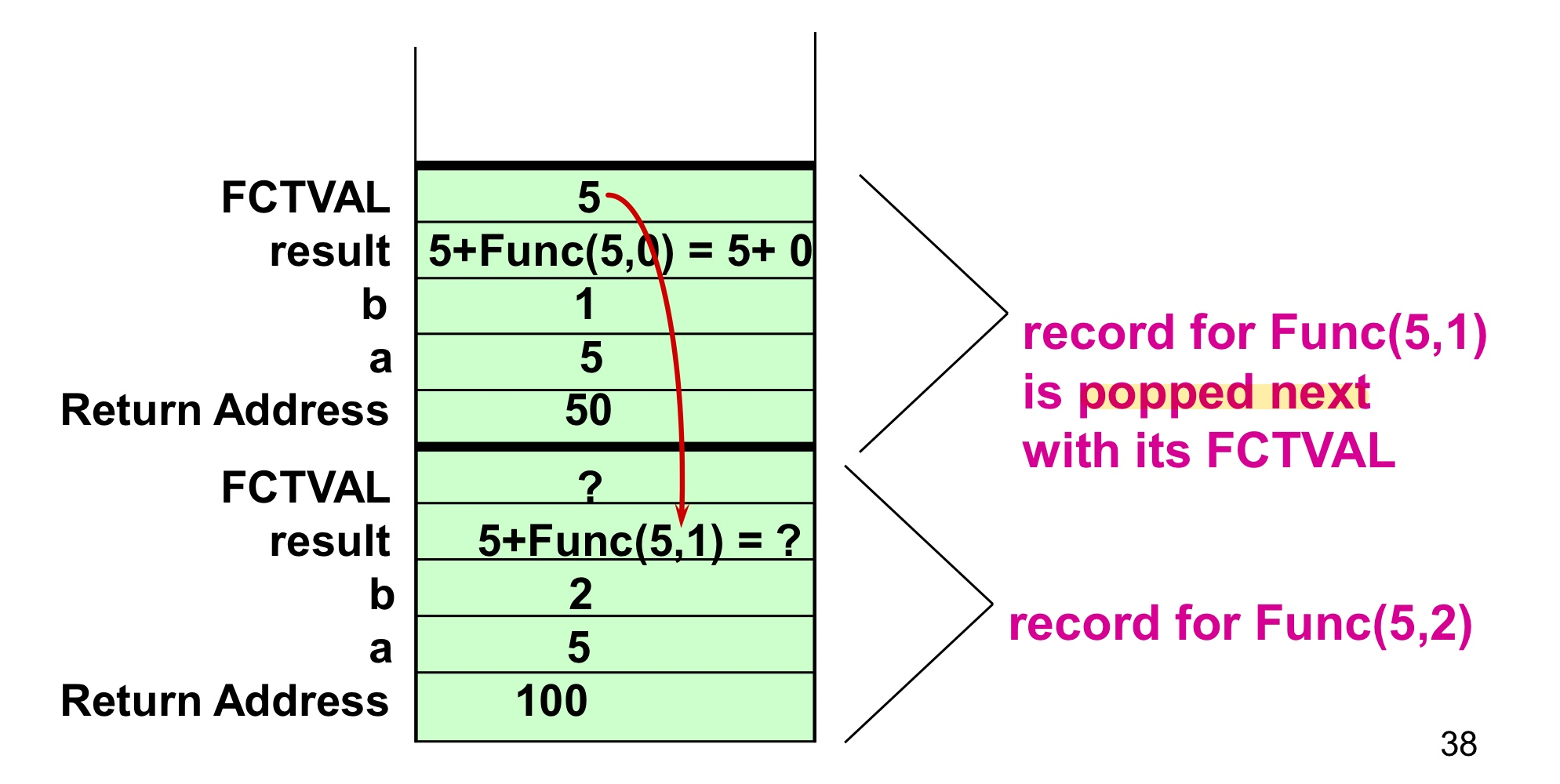
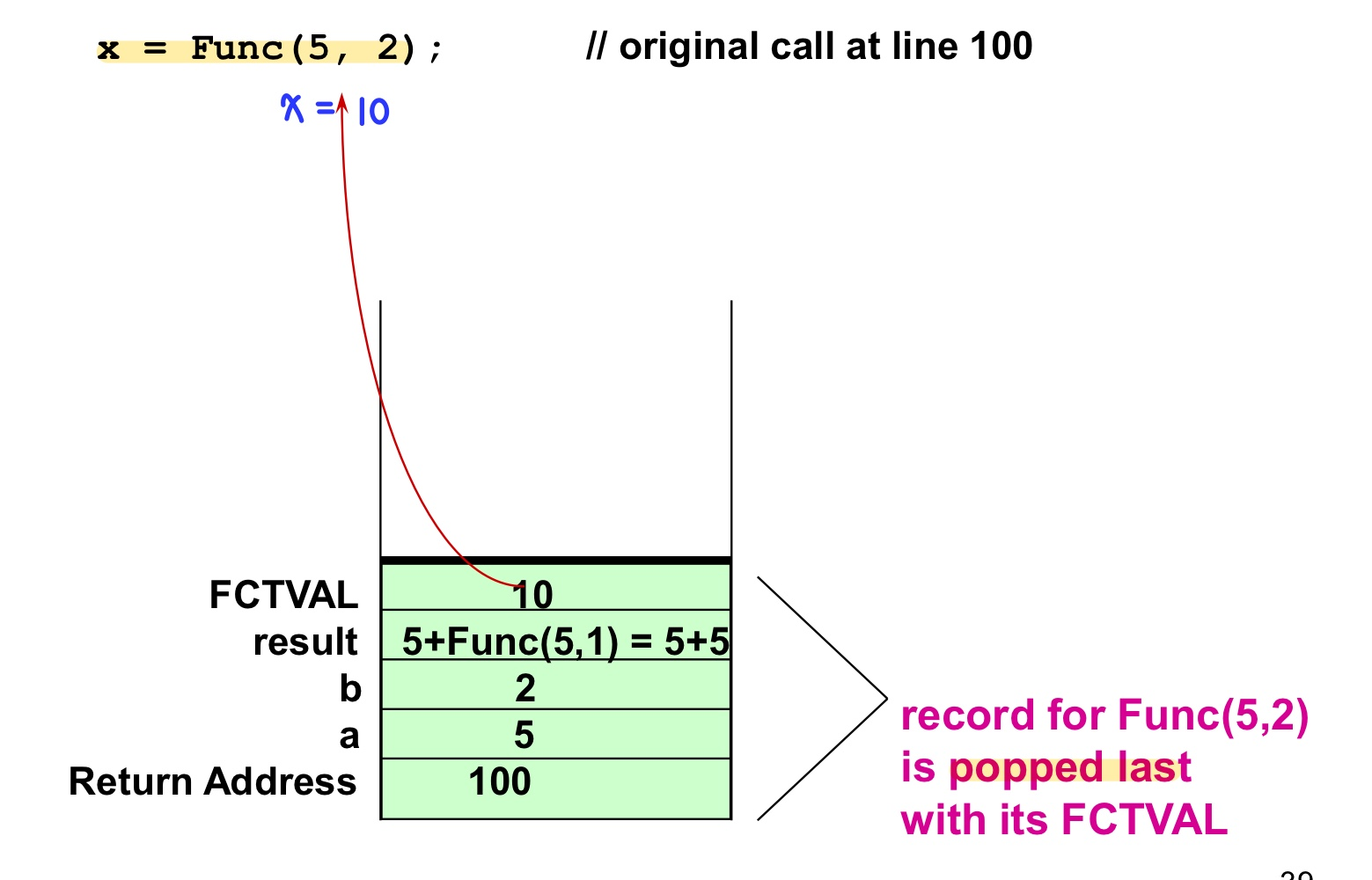
- 코드


와!! 정말 깔끔하게 정리가 잘 되어 있네요ㅎㅎ 잘 보고 갑니다~