[자료구조] Tree - 개요 (기본 개념과 구현)

Kyung Jae, Cheong·2024년 10월 16일
Javapython자료구조
1

자료구조-DataStructure

목록 보기
12/19
post-thumbnail

본 시리즈는 프로그래밍 자료구조의 개념을 정리하고 실습을 진행해보는 시리즈입니다.

  • 실습은 다음과 같은 개발환경 및 버전에서 진행하였습니다.
    • IDE : IntelliJ IDEA (Ultimate Edition)
    • Java : JDK 21 (corretto-21)
    • Python : 3.9 (conda env)

트리(Tree) 자료구조 - 개요

1. Tree란?

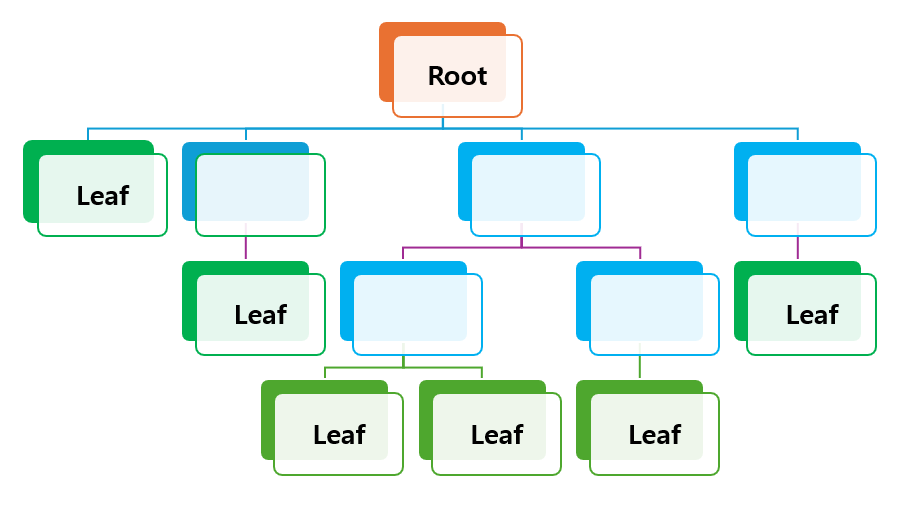
트리(Tree)는 계층적인 구조를 표현하는 비선형 자료구조입니다.

  • 그래프의 일종으로, 트리는 정점(Node)과 간선(Edge)으로 이루어져 있지만, 특별히 사이클이 없는 계층적 구조를 가집니다.

1.1 Tree의 주요 특징

  • 계층적 구조: 트리는 루트 노드(최상단 노드)에서 시작해 자식 노드(아래 방향)들로 뻗어 나가는 계층적 자료구조로, 데이터를 논리적이고 구조화된 방식으로 표현할 수 있습니다.

    • 루트 노드(Root Node): 트리의 최상단 노드로, 트리의 시작점이 됩니다.

      • 모든 다른 노드는 루트 노드로부터 이어지며, 트리에는 하나의 루트 노드만 존재합니다.

    • 부모-자식 관계: 트리에서 각 노드는 부모(Parent) 노드와 자식(Child) 노드의 관계를 형성합니다.

      • 상위 노드가 하위 노드로 이어져 트리 구조를 만듭니다.

    • 리프 노드(Leaf Node): 자식 노드가 없는 노드를 리프 노드라고 부르며, 트리의 말단을 의미합니다.

  • 비순환성(Acyclic): 트리는 사이클(순환)이 없는 비순환 구조입니다.

    • 즉, 트리 내부에서 루프가 발생하지 않으며, 부모 노드와 자식 노드간의 이동만 가능합니다.

  • 연결성(Connectedness): 트리의 모든 노드는 루트 노드에서 단 하나의 경로로 연결됩니다.

    • 따라서 트리는 하나의 연결된 그래프로 볼 수 있습니다.

트리는 이러한 특징들 덕분에 디렉토리 구조, 데이터베이스 인덱스 등 계층적인 데이터 관리와 탐색에 널리 사용됩니다.

1.2 Tree의 용도

트리는 다양한 분야에서 데이터의 계층적 구조를 표현하는 데 유용하며, 특히 다음과 같은 주요 용도로 사용됩니다.

  • 파일 시스템 구조: 트리는 디렉토리 구조와 파일 시스템을 표현하는 데 사용됩니다.

    • 루트 디렉토리에서 시작하여 하위 폴더와 파일로 뻗어 나가는 구조는 트리와 동일한 원리입니다.

  • 데이터베이스 인덱스: 트리는 데이터베이스 인덱싱에서 효율적인 검색을 위해 사용됩니다.

    • 예를 들어, B-Tree와 B+Tree는 대규모 데이터베이스에서 빠른 검색과 정렬을 가능하게 해줍니다.

  • 컴파일러 구조: 트리는 컴파일러가 구문 분석 시 프로그램의 구조를 나타낼 때 사용됩니다.

    • 구문 분석 트리(Syntax Tree)는 프로그램의 문법 구조를 트리 형태로 표현합니다.

  • 이진 탐색 트리(Binary Search Tree, BST): 이진 트리는 검색 속도를 개선하기 위해 활용됩니다.

    • 특히, BST는 정렬된 데이터를 저장하여 빠른 검색, 삽입, 삭제 연산을 수행할 수 있습니다.

  • 네트워크 라우팅: 트리는 네트워크에서 효율적인 경로 탐색 및 패킷 전달을 위해 사용되며, 최소 신장 트리(MST) 같은 알고리즘으로 네트워크 연결을 최적화할 수 있습니다.

  • 게임 및 AI: 트리는 게임 트리, 의사결정 트리(Decision Tree) 등의 구조로 활용되며, AI와 머신러닝 분야에서는 의사결정 트리(Decision Tree)와 같은 알고리즘이 사용됩니다.

트리는 그 특유의 계층성 덕분에 데이터의 구조화, 탐색, 최적화 등 다양한 문제를 해결하는 데 중요한 역할을 합니다.

1.3 Tree와 Graph의 비교

트리는 그래프의 특수한 형태로, 두 자료구조는 기본적으로 비슷한 점이 있지만 몇 가지 차이점이 있습니다.

비교 항목TreeGraph
구조계층적 구조
(루트에서 자식 노드로 이어짐)		일반적인 네트워크 구조
(정점 간의 다양한 연결 가능)
루트 노드단 하나의 루트 노드가 존재특정 루트 노드가 없음
(모든 노드가 동등)
부모-자식
관계		노드 간 명확한 부모-자식 관계 존재부모-자식 관계 없이 노드 간 자유로운 연결
순환성비순환성 (사이클이 없음)사이클이 존재할 수 있음
연결성루트 노드에서 단일 경로로 모든 노드가 연결됨모든 노드가 여러 경로로 연결될 수 있음
용도파일 시스템, 데이터베이스 인덱스 등
계층적인 데이터 표현		네트워크 모델링, 소셜 네트워크, 지도 등
다양한 분야에서 사용

Tree는 Graph의 특수한 형태로, 사이클이 없고 명확한 부모-자식 관계를 가진 계층적 구조입니다.

  • 반면 Graph는 좀 더 일반적인 구조로, 사이클과 다중 경로를 허용하며 네트워크 모델링에 주로 사용됩니다.

이러한 차이 덕분에 트리는 계층적 데이터를 표현하거나 탐색하는 데 적합한 자료구조이고, 그래프는 복잡한 네트워크나 연결성을 분석하는 데 적합한 자료구조입니다.

2. Tree의 구조 및 용어

트리의 기본적인 구조와 용어를 이해하는 것은 트리 자료구조를 효과적으로 활용하는 데 매우 중요합니다.

  • 트리는 노드(Node)와 그 노드들을 연결하는 간선(Edge, Link, Branch)으로 이루어진 계층적 구조를 가지며, 각 구성 요소마다 중요한 역할을 합니다.

여기에서는 트리에서 자주 사용되는 용어들을 정리합니다.

2.1 노드(Node)

  • 노드(Node)는 트리에서 데이터를 저장하는 기본 단위입니다.
  • 트리의 각 노드는 데이터를 포함하며, 다른 노드들과의 부모-자식 관계를 형성할 수 있습니다.
  • 간선(Edge)는 트리에서 노드 간의 연결을 나타내는 선입니다.
    - 간혹 Link, Branch라는 용어로도 불립니다.
  • 트리에서는 각 간선이 부모 노드와 자식 노드를 연결하며, 단방향성을 가집니다.

2.3 루트 노드(Root Node)

  • 루트 노드(Root Node)는 트리의 최상단에 위치한 노드로, 트리의 시작점입니다.
  • 트리에는 단 하나의 루트 노드만 존재하며, 이 루트 노드는 트리의 모든 다른 노드들과 경로로 연결되어 있습니다.
  • 부모가 없는 유일한 노드입니다.

2.4 리프 노드(Leaf Node)

  • 리프 노드(Leaf Node)는 자식이 없는 노드로, 트리의 말단을 의미합니다.
  • 트리의 탐색이 끝나는 지점을 나타내며, 다른 노드로 더 이상 연결되지 않습니다.

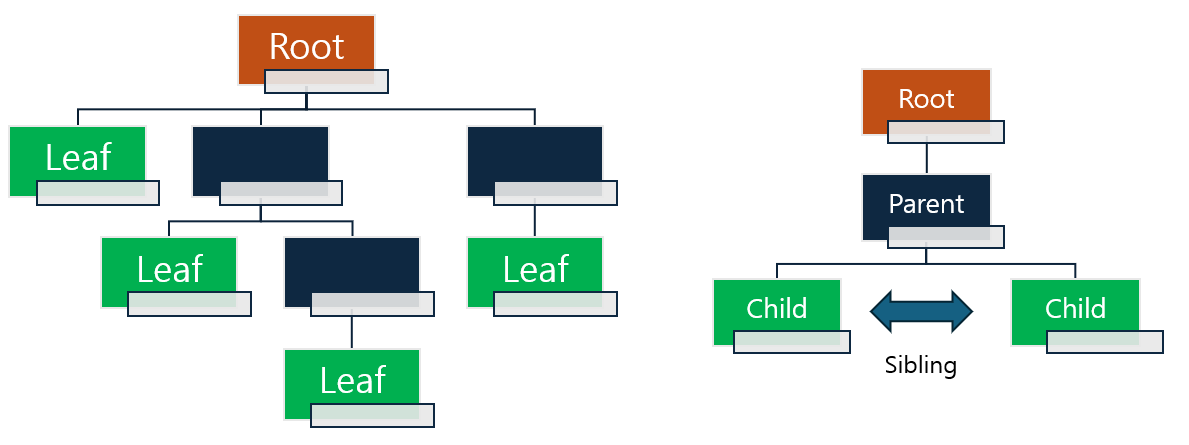
2.5 부모 노드(Parent Node)와 자식 노드(Child Node)

  • 부모 노드(Parent Node)는 다른 노드를 연결하고 있는 상위 노드를 말하며, 연결된 하위 노드를 자식 노드(Child Node)라고 합니다.
  • 한 부모 노드는 여러 자식 노드를 가질 수 있지만, 한 자식 노드는 반드시 하나의 부모 노드만 가집니다.

2.6 형제 노드(Sibling Nodes)

  • 형제 노드(Sibling Nodes)는 같은 부모 노드를 공유하는 노드들입니다.
  • 같은 레벨(Level)에 있는 노드들이며, 서로 인접한 관계로 묶여 있습니다.
    • 위치가 인접하다는 것일뿐, 그래프에서의 인접의 개념과는 다른 의미입니다.

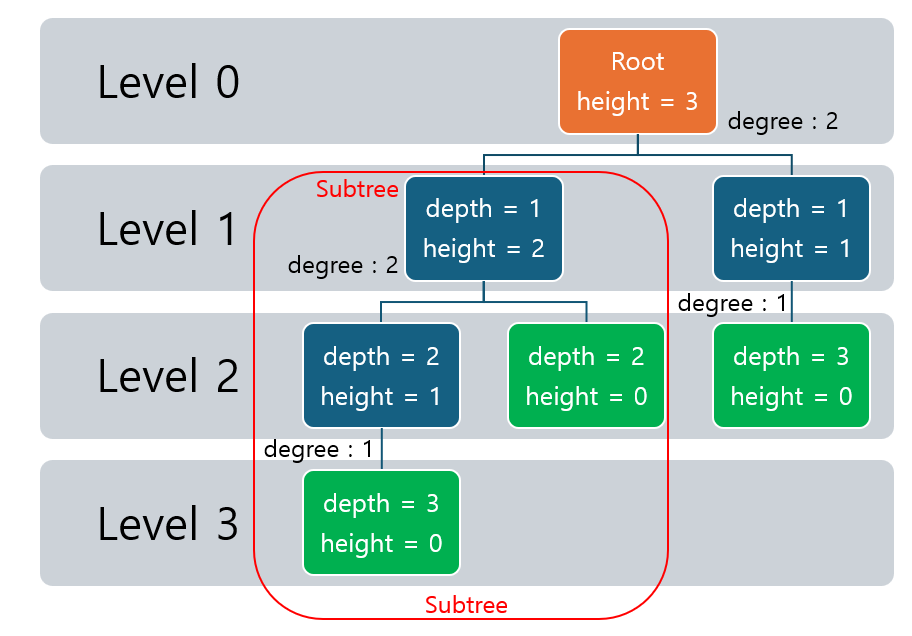
2.7 서브트리(Subtree)

  • 서브트리(Subtree)는 트리 내의 어느 한 노드를 루트로 하는 트리를 말합니다.
  • 트리의 각 노드는 자신을 루트로 하는 하위 트리(서브트리)를 형성할 수 있습니다.

2.8 깊이(Depth)

  • 깊이(Depth)는 특정 노드가 루트 노드로부터 떨어진 거리를 나타냅니다.
  • 루트 노드의 깊이는 0이며, 각 노드의 깊이는 그 부모 노드의 깊이보다 1만큼 큽니다.

2.9 레벨(Level)

  • 레벨(Level)은 루드노드를 기준으로 하는 트리의 깊이를 의미하며, 루트 노드는 0레벨, 그 아래로 내려갈수록 레벨이 1씩 증가합니다.
  • 같은 레벨에 있는 노드들은 같은 깊이를 가지며, 부모 노드가 같다면 이들은 서로 형제노드가 됩니다.

2.10 높이(Height)

  • 높이(Height)는 특정 노드에서 리프 노드까지의 가장 긴 경로 (즉, 자식 노드로 내려가는 최대 깊이)를 의미합니다.
    • 리프 노드의 높이는 0이며, 부모 노드의 높이는 자식 노드의 높이보다 1만큼 큽니다.
    • 루트 노드의 높이는 트리 전체의 높이와 동일합니다.
  • 트리의 높이는 루트 노드의 높이를 의미하며, 이는 트리에서 가장 깊은 노드까지의 경로 길이와 같습니다.

2.11 차수(Degree)

  • 차수(Degree)는 하나의 노드가 가지고 있는 자식 노드의 수를 나타냅니다.
  • 트리의 최대 차수를 가지는 노드가 트리의 차수와 동일합니다.
    • 참고로 트리의 최대 차수가 2인 트리를 이진트리(Binary Tree)라고 부릅니다.
    • 이진트리는 다뤄야할 내용이 많아서 다음 포스팅에서 자세히 다룹니다.

3. 일반 Tree 구현 (Java, Python)

이번 섹션에서는 트리(Tree) 자료구조를 Java와 Python에서 어떻게 구현할 수 있는지 다루어 보겠습니다.

  • 기본적으로 트리는 노드(Node)와 자식 노드(Child Nodes)로 이루어진 구조로, 이를 표현하기 위해 두 언어에서 각각 클래스 기반의 구현을 사용합니다.
  • 여기서는 간단한 트리 생성과 트리 순회(Traversal) 알고리즘을 다루어 보겠습니다.

3.1 Java에서 Tree 구현

Java에서는 클래스 기반으로 트리를 구현하며, 노드 클래스(Node)와 트리 클래스(Tree)를 따로 만들어 트리 구조를 정의합니다.

3.1.1 노드 클래스(Node Class)

먼저, 트리의 기본 단위인 노드를 정의합니다.

  • 각 노드는 데이터와 자식 노드 리스트를 가지며, 자식 노드들을 저장하는 List를 사용하여 구현할 수 있습니다.
import java.util.ArrayList;
import java.util.List;

class Node {
    String data;
    List<Node> children;

    // 노드 생성자
    public Node(String data) {
        this.data = data;
        this.children = new ArrayList<>();
    }

    // 자식 노드 추가
    public void addChild(Node child) {
        this.children.add(child);
    }
}

3.1.2 트리 클래스(Tree Class)

트리의 루트를 관리하고, 트리 전체를 탐색하는 기능을 포함하는 트리 클래스를 정의합니다.

class Tree {
    Node root;

    // 트리 생성자 (루트 노드를 설정)
    public Tree(String rootData) {
        root = new Node(rootData);
    }

    // 전위 순회 (Pre-order Traversal)
    public void traversePreOrder(Node node) {
        if (node != null) {
            System.out.print(node.data + " ");
            for (Node child : node.children) {
                traversePreOrder(child);
            }
        }
    }
}
  • 여기서 전위 순회 (Pre-order Traversal)는 부모노드 -> 왼쪽 ~ 오른쪽 자식노드 순서로 트리를 재귀적으로 순회하는 알고리즘인데, 주로 트리 차수가 2인 이진트리에서 자주 사용하는 알고리즘입니다.
    • 자세한건 다음 포스팅인 이진트리 파트에서 다루도록 하겠습니다.

3.1.3 트리 생성 및 탐색

이제 트리를 생성하고 탐색을 수행해보겠습니다.

public class Main {
    public static void main(String[] args) {
        // 트리 생성
        Tree tree = new Tree("Root");
        Node child1 = new Node("Child1");
        Node child2 = new Node("Child2");

        tree.root.addChild(child1);
        tree.root.addChild(child2);

        Node grandChild1 = new Node("GrandChild1");
        Node grandChild2 = new Node("GrandChild2");
        child1.addChild(grandChild1);
        child2.addChild(grandChild2);

        // 전위 순회
        System.out.println("Pre-order Traversal:");
        tree.traversePreOrder(tree.root);  // 출력: Root Child1 GrandChild1 Child2 GrandChild2
    }
}

위 코드에서 전위 순회(Pre-order Traversal)를 수행하면, 트리의 루트 노드부터 시작하여 자식 노드들을 왼쪽에서 오른쪽으로 차례로 탐색합니다.

3.2 Python에서 Tree 구현

Python에서도 트리를 클래스 기반으로 구현합니다.

  • 기본적으로 Node 클래스와 Tree 클래스를 나누어 트리 구조를 정의하고, 이를 통해 트리의 데이터를 관리하고 탐색합니다.

3.2.1 노드 클래스(Node Class)

Python에서 노드를 정의하는 방법은 매우 간단합니다.

  • 각 노드는 데이터와 자식 노드 리스트를 가집니다.
class Node:
    def __init__(self, data):
        self.data = data
        self.children = []

    # 자식 노드 추가
    def add_child(self, child):
        self.children.append(child)

3.2.2 트리 클래스(Tree Class)

이제 트리 클래스를 정의하여 트리 전체를 관리하고 탐색 기능을 구현합니다.

class Tree:
    def __init__(self, root_data):
        self.root = Node(root_data)

    # 전위 순회 (Pre-order Traversal)
    def traverse_preorder(self, node):
        if node:
            print(node.data, end=' ')
            for child in node.children:
                self.traverse_preorder(child)

3.2.3 트리 생성 및 탐색

Python에서도 트리를 생성하고 탐색을 수행해보겠습니다.

# 트리 생성
tree = Tree("Root")
child1 = Node("Child1")
child2 = Node("Child2")

tree.root.add_child(child1)
tree.root.add_child(child2)

grandchild1 = Node("GrandChild1")
grandchild2 = Node("GrandChild2")
child1.add_child(grandchild1)
child2.add_child(grandchild2)

# 전위 순회
print("Pre-order Traversal:")
tree.traverse_preorder(tree.root)  # 출력: Root Child1 GrandChild1 Child2 GrandChild2

Python에서는 print() 문을 사용하여 각 노드를 출력하고, 전위 순회(Pre-order Traversal) 방식으로 트리의 모든 노드를 탐색합니다.

3.3 트리 순회 방법 소개

트리 자료구조는 탐색 알고리즘에서 중요한 역할을 하며, 대표적인 트리 순회(Traversal) 방법에는 다음 세 가지가 있습니다.

  1. 전위 순회 (Pre-order Traversal): 루트 노드를 먼저 방문하고, 그 후 자식 노드를 왼쪽에서 오른쪽 순서로 방문합니다.
  2. 중위 순회 (In-order Traversal): 왼쪽 자식 노드를 먼저 방문하고, 그 후 루트 노드를 방문하며, 마지막으로 오른쪽 자식 노드를 방문합니다. (주로 이진 트리에서 사용)
  3. 후위 순회 (Post-order Traversal): 자식 노드들을 먼저 방문하고, 그 후 루트 노드를 방문합니다.

위 예시에서는 전위 순회만을 다뤘지만, 필요에 따라 중위나 후위 순회 방식도 추가적으로 구현할 수 있습니다.

  • 자세한 사항은 다음 포스팅인 이진 트리(Binary Tree)파트에서 자세히 다룰 예정입니다.

마무리

이번 포스팅에서는 트리 자료구조의 기본 개념과 구현 방법에 대해 살펴보았습니다.

  • Java와 Python에서 트리를 어떻게 만들고 탐색할 수 있는지를 알아보았으며, 특히 전위 순회(Pre-order Traversal) 방식을 예시로 다루어 보았습니다.
    • 트리 순회 방법은 전위 순회 외에도 중위 순회, 후위 순회 등이 있으며, 이들은 트리의 탐색 방식에 따라 다양한 응용이 가능합니다.

트리는 파일 시스템, 데이터베이스 인덱스, 게임 개발 등 다양한 분야에서 활용되며, 데이터를 계층적으로 표현하는 데 매우 유용한 자료구조입니다.

다음 포스팅에서는 트리의 특수한 형태인 이진 트리(Binary Tree)를 다루며, 다양한 탐색 알고리즘과 활용 사례들을 알아보겠습니다.

profile
Kyung Jae, Cheong
일 때문에 포스팅은 잠시 쉬어요 ㅠ 바쁘다 바빠 모두들 화이팅! // Machine Learning (AI) Engineer & BackEnd Engineer (Entry)
이전 포스트

[자료구조] NonLinear Data - Graph [Part2. 표현 및 구현]

다음 포스트

[자료구조] Tree - Binary Tree (이진 트리) - 개념과 구현

0개의 댓글