cs231n 과제2 Q2- Batch Normalization

이준학·2024년 7월 17일

Assignment2 Backpropagation Batch Normalization Layer Normalization cs231n q2

cs231n 과제

목록 보기

7/15

이번 글에서는 cs231n 과제2 Q2에 대해서 다뤄보려고 한다. Q2는 Batch normalization를 구현하고, 이를 이전에 구현했던 fc_net.py에 반영하는 내용이다. 또, Batchnorm의 단점을 해결해줄 수 있는 LayerNorm에 대한 구현도 한다. 헷갈리는 부분이 많아서 시간이 역시나 오래 걸렸다.

1. Batch Normalization Forward/Backward pass

이 부분에서 어려웠던 부분은 backward pass이다. forward pass는 그냥 논문에 나온대로 계산하면 된다. 그런데 backward pass를 계산할 때는 computational graph를 그려서 직접 backprop 식을 계산해야 하기 때문에 헷갈리는 부분들이 많았다. 결과적으로 아래와 같이 계산을 하고, 코드에 반영하면 된다. 자세한 내용은 아래 블로그 링크를 참고하면 될 것 같다.

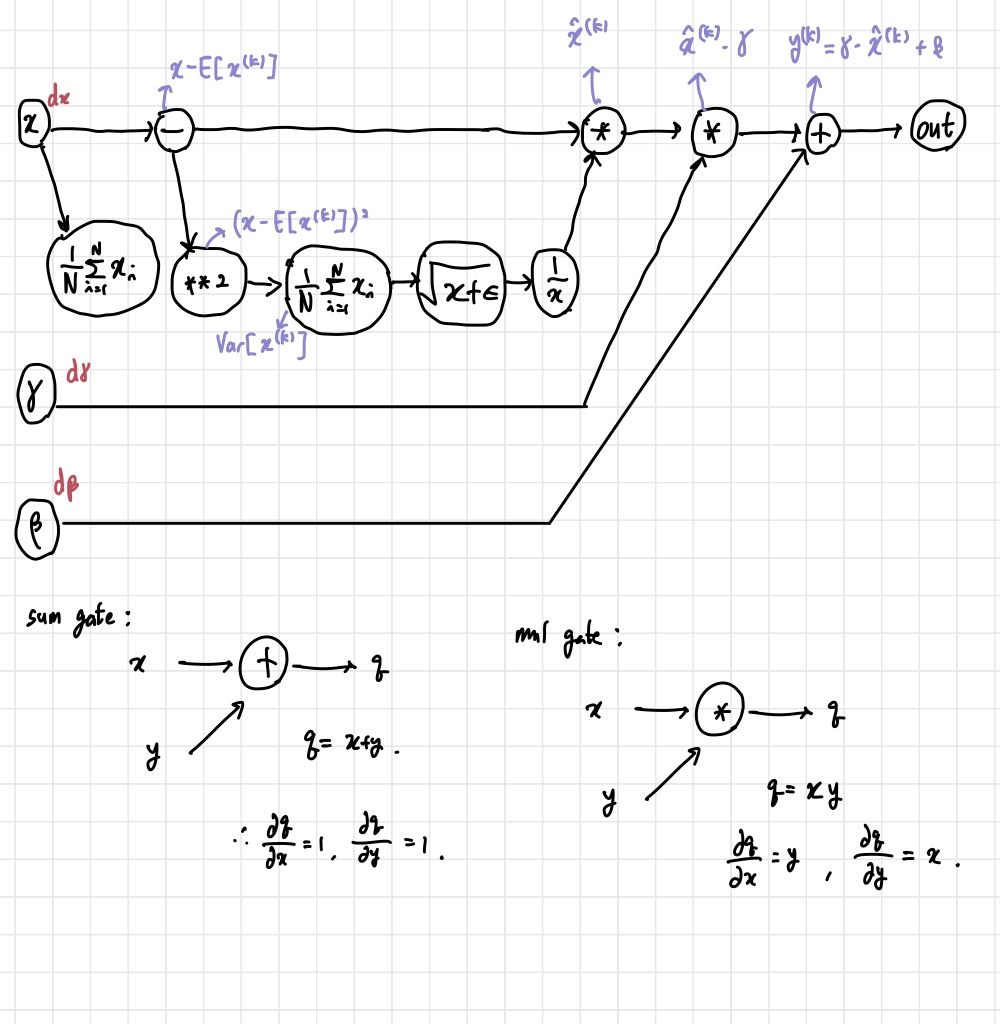
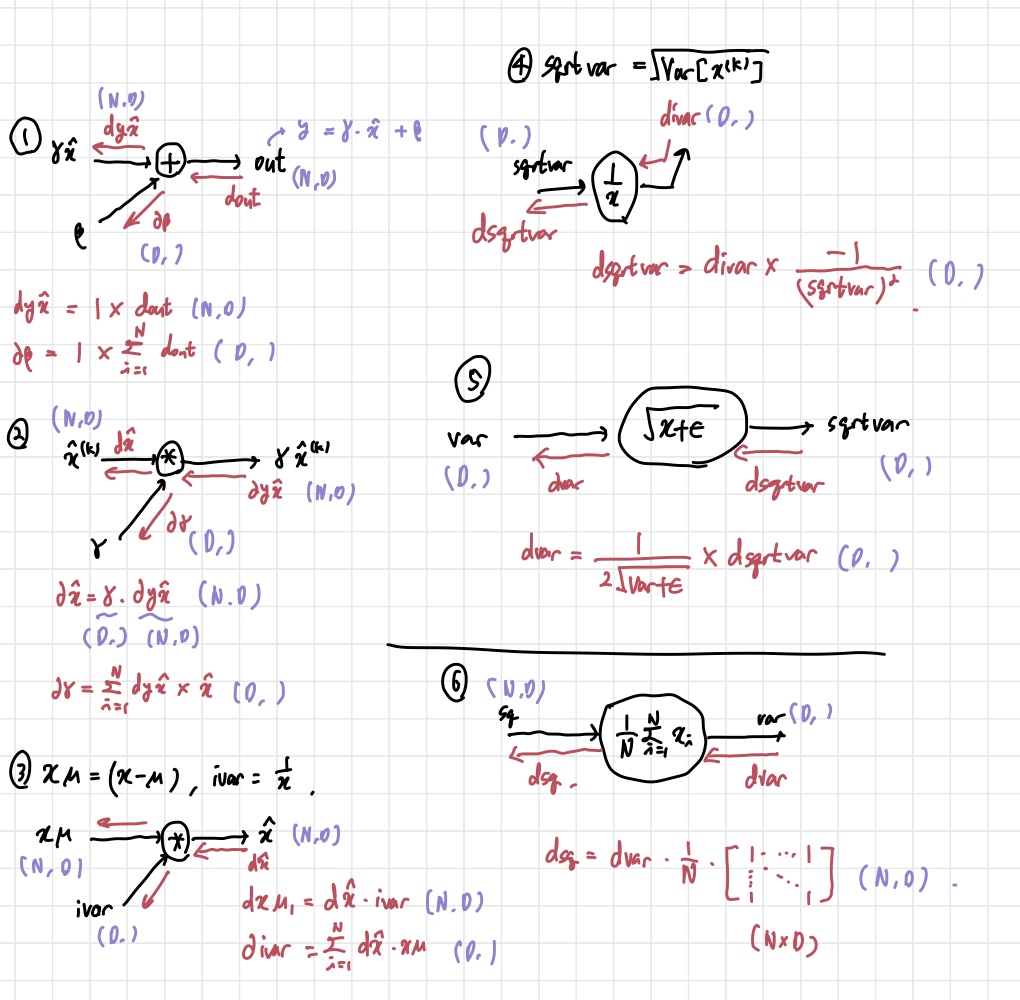
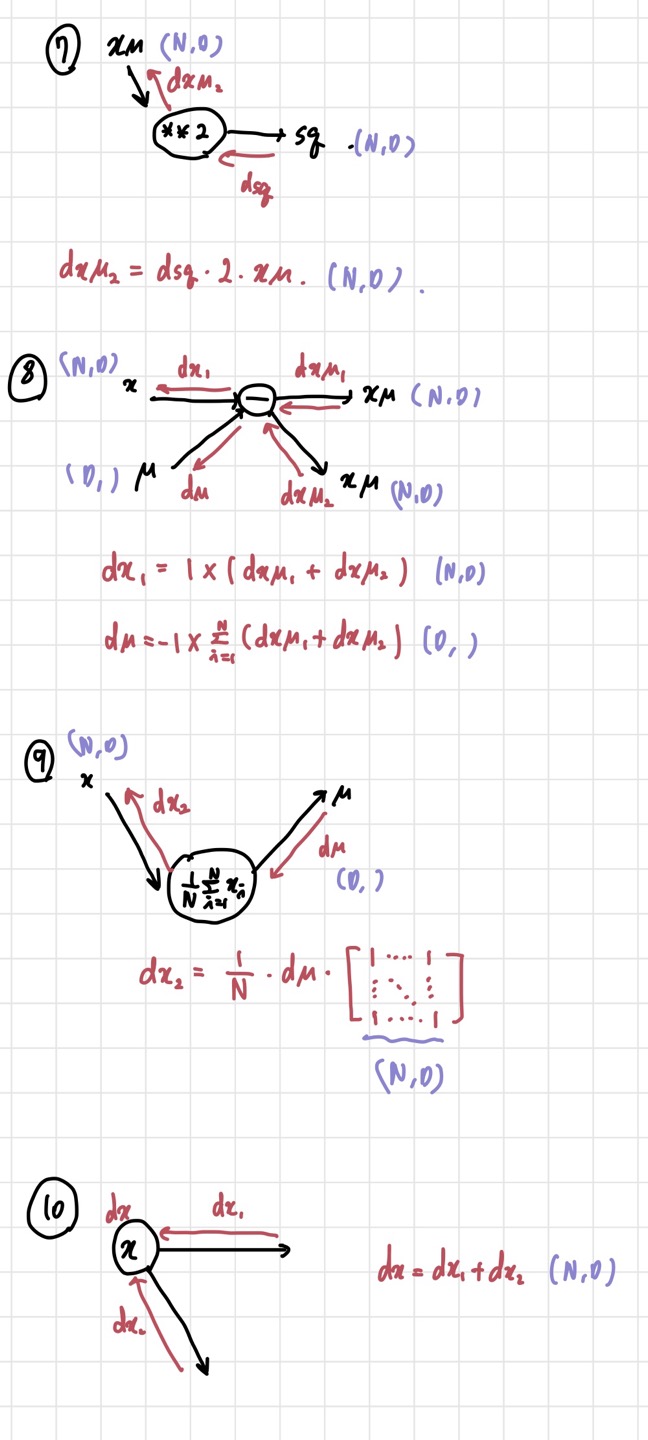
2. Layer Normalization

사실 코드는 batch normalization의 코드와 굉장히 유사하다. 그러나 나는 layer normalization의 개념에 대해 자세하게 몰랐기 때문에 헤맸다. 논문을 봐도 직관적인 이해가 힘들었다. 키 포인트는 Batch Normalization과 Layer Normalization이 어떻게 다른지를 아는 것이다.

Layer Norm vs Batch Norm

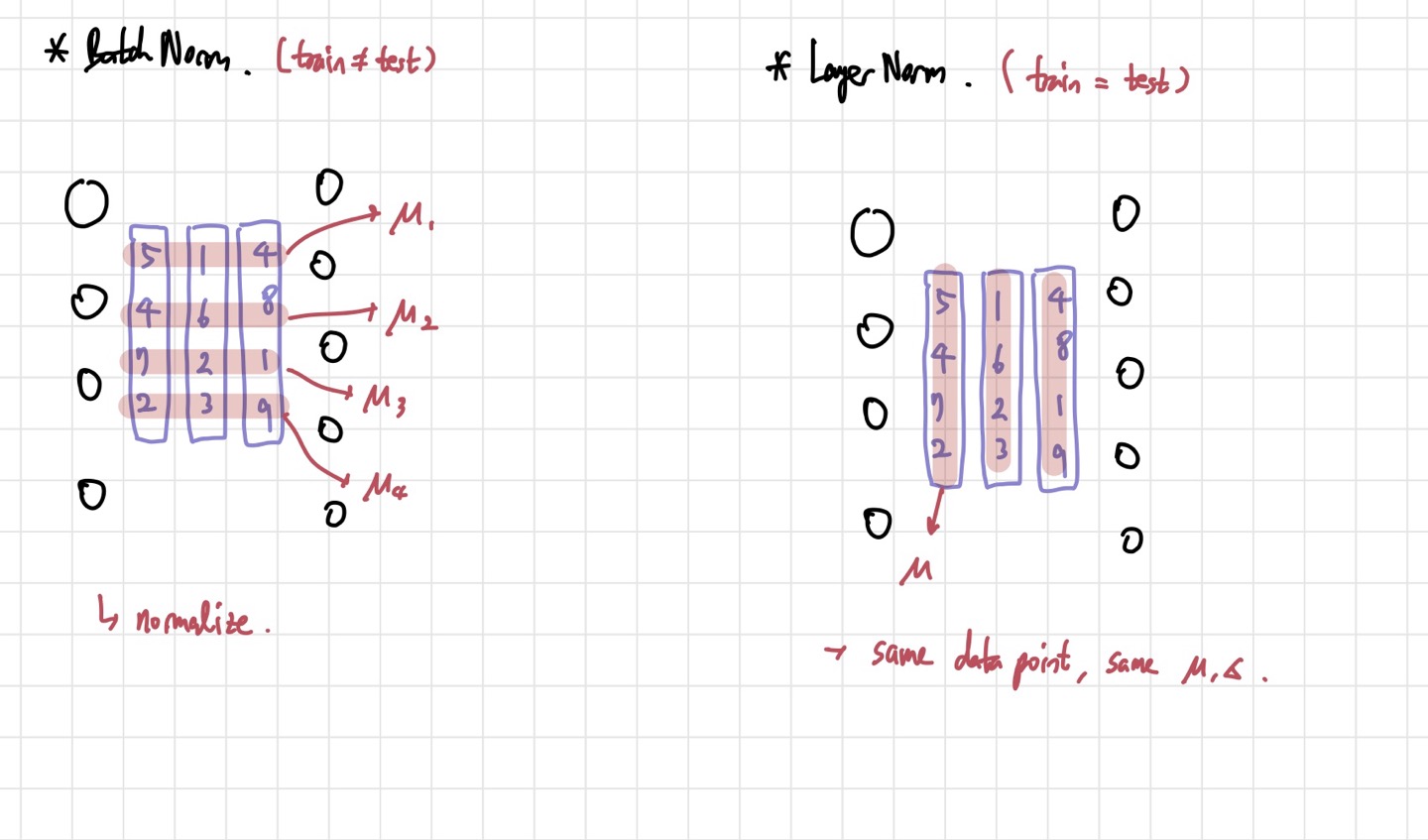
둘의 가장 큰 차이는 평균과 분산을 어떻게 구하는지이다. 나머지는 비슷하다. 위의 사진과 같이 나오게 된다. Batch Normalization의 경우, 각 activation에 대해 평균과 분산을 계산한다. 또한, Mini-Batch statistics를 따르기 때문에, batch size가 너무 커지거나 너무 작아지면 성능이 좋지 않다. 반면에 Layer Normalization은 feature별로 평균과 분산을 계산한다. 결과적으로 하나의 layer에서 training example이 같다면, 모든 activation이 하나의 평균과 분산을 공유하는 것이다. BN의 단점인 batch size에 대한 민감성이 사라지게 되어 좋은 결과를 얻을 수 있다. RNN에서 특히 더 좋은 성능을 낸다고 한다.
이러한 차이가 있기 떄문에, 코드 상에서 np.sum할 때 axis만 잘 수정해준다면 어렵지 않게 해결할 수 있다.

def batchnorm_forward(x, gamma, beta, bn_param):
             ....
             ....
        x_mean=x.mean(axis=0) # gives (D,), which is the mean for each feature.(sample mean)
        x_var=x.var(axis=0) # same shape as x_mean. feature-wise variance. (sample variance)
        x_std=np.sqrt(x_var+eps)
        x_hat=(x-x_mean)/x_std
        out=gamma*x_hat+beta
        ....
        ....

def layernorm_forward(x, gamma, beta, ln_param):
    ....
    ....
    x_mean=x.mean(axis=1).reshape(-1,1) # gives (N,), which is the mean for each feature.(sample mean)
    x_var=x.var(axis=1).reshape(-1,1) # same shape as x_mean. feature-wise variance. (sample variance)
    x_std=np.sqrt(x_var+eps).reshape(-1,1)
    x_hat=(x-x_mean)/x_std
    out=gamma*x_hat+beta
    cache = x, x_mean, x_var,x_std, gamma, x_hat
   ....
   ....