
- 윤덕호 저서 파이썬 날코딩으로 알고 짜는 딥러닝을 공부하고 개인적으로 정리한 글입니다.
- 사진, 내용, 코드는 책을 참고한 것입니다. 코드는 오픈소스로 저저의 깃허브에 모두에게 공개되어있습니다.
단층 퍼셉트론 신경망의 구조
- 일련의 퍼셉트론을 한 줄로 배치하여 입력 벡터 하나로부터 출력 벡터 하나를 얻어내는 구조(은닉 계층 없이 출력 계층만 존재하는)
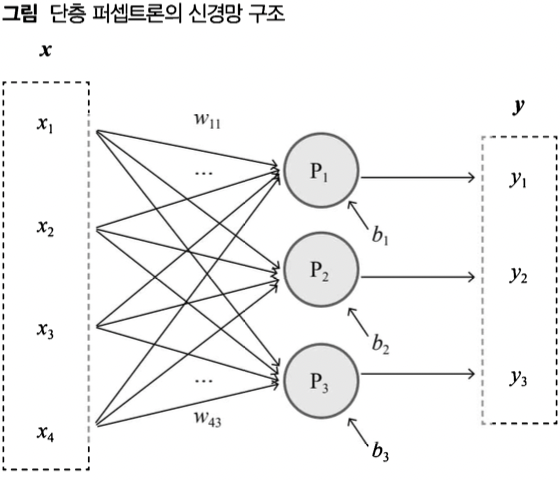
- 각각의 퍼셉트론은 입력벡터만 공유할 뿐 사이에는 어떤 영향도 주고받지 않음
- 가중치 행렬 W, 편향 백터 b가 존재함; 실제로 행렬로 한꺼번에 처리함
- 높은 수준의 문제 해결력은 없음
텐서 연산과 미니배치의 활용
- 텐서는 다차원 숫자 배열 정도로 이해하면 됨(0차원 스칼라, 1차원 벡터, 2차원 행렬, 3차원 이상 숫자 배열 모두 텐서)
- 반복문 대신 텐서를 사용하는 것이 처리 속도가 빠르기 때문에 텐서를 사용함
- 이는 병렬수치 연산이기 때문에 GPU 이용환경에서 속도 차이가 커짐
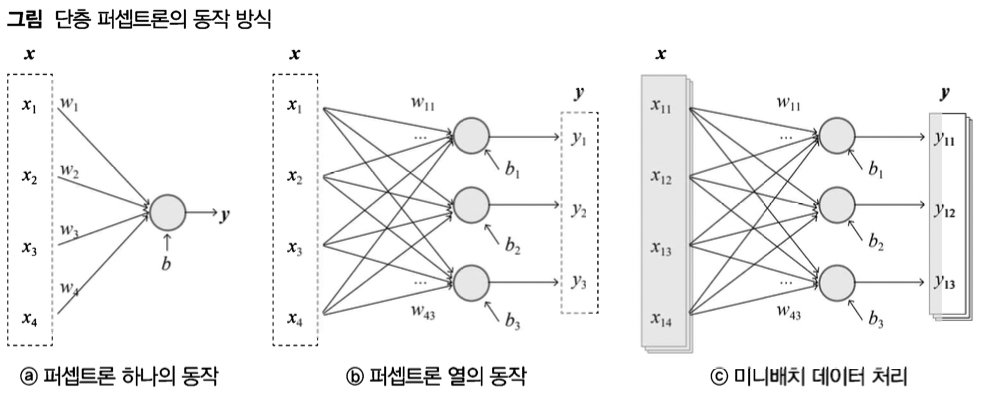
- 단층 퍼셉트론은 보통 c처럼 구성되어 있음
- 위와 같이 반복분이 아닌 내적 연산을 통해 계산
- 입력 성분을 일차식으로 표현 가능하면 선형 연산 / 불가능하면 비선형 연산
- 그림a $$ y = x_1w_1 + ... + x_nw_n + b = xw + b$$
- 그림b $$ yi = x_1w{i1} + ... + xnw{ni} + b = xw_i+b = xW+b$$
- 그림c $$ y_j = x_jW+b = XW+b$$
- 미니 배치: 전체 데이터 셋을 몇 개의 데이터 셋으로 나누었을 때, 그 작은 데이터 셋 뭉치
- 에포크(epoch): 학습 데이터 전체에 대한 한 차례의 처리
신경망의 세 가지 기본 출력 유형과 회귀 분석
- 인공지능 알고리즘의 출력 내용은 회귀분석, 이진판단, 선택분류로 구성되어있음
- 회귀(regression)이란 옛날 상태로 돌아간다는 뜻, 조사집단의 평균값으로 돌아가려는 경향이 있다
회귀 분석과 평균제곱오차(MSE) 손실 함수
- 평균제곱오차(Mean Squared Error): 각 성분에 대한 추정값과 정답 사이의 오차를 제곱 후 평균을 내는것
- 정확해질 수록 작아지는 성질, 미분이 가능한 평가지표로 정의됨, 이러한 평가지표를 손실 함수(Loss Function), 비용 함수(Cost Function)이라고 함
- 평균 오차 합을 사용하지 않는 이유는 미분을 할 수 없기 때문임
경사하강법과 역전파
-
경사하강법: 함수의 기울기를 반복적으로 계산하면서 이 기울기에 따라 함수값이 낮아지는 방향으로 이동하는 알고리즘 (손실함수, 비용함수를 대상으로), 순전파와 역전파를 반복하며 파라미터를 변경해 나감
-
순전파: 입력 데이터에 대해 신경망 구조를 따라가면서 현재 파라미터를 이용해 손실함숫값을 계산
-
역전파: 순전파의 계산과정울 역순으로 거슬러 올라가면서 손실 함수값에 대해 영향을 미친 모든 성분에 대하여 손실 기울기를 계산함 (선형대수학 중 연쇄법칙 사용)
-
파라미터 성분에 대해서 계산된 손실 기울기를 이용해 값을 변경시킴
-
학습율(alpha)이라는 하이퍼 파리미터를 이용
-
-
-
편미분을 사용/ 전미분은 x가 다른 변수에 미치는 직 간접적인 영향까지 모두 따지는 반면 편미분은 직접적인 영향만 따짐
-
난수함수를 사용해 초기 파라미터 값을 초기화 함
-
Local Minimum을 해결할 만한 보조 기법들이 필요 ex)adam
신경망의 구성
- input data: GIGO
- 중간 계산결과
- 파라미터: 역전파와 경사 알고리즘을 통한 지속적 수정
- 하이퍼 파라미터: 학습률, 학습 횟수, 미니 배치 크기 등 딥러닝 모델의 구조나 학습 과정에 영향을 미치는 상숫값
원-핫 벡터 표현
- 비선형 정보를 항목별로 분할하여 해당하는 1, 해당하지 않는 0으로 나타내는 방식
- 단층 퍼셉트론의 처리과정에서는 비선형 함수가 사용되지 않기 때문에 비선형 특성을 포착하지 못하고 원-핫 벡터 표현은 이를 보완해준다
구현 코드 및 Annotation
전복의 고리 수 추정 신경망
- 전복 나이를 알아내는 데 이용하는 껍질의 고리 수를 추정하는 회귀 분석 신경망
- 단층 퍼셉트론으로 구현
- Data : Abalone Data (Kaggle)
- 4177마리의 전복(rows)
- 8가지의 특성(columns)
- 껍질의 고리 수(target)
- 라이브러리 및 사전 값 정의
import numpy as np
import csv
import time
np.random.seed(1234)
def randomize(): np.random.seed(time.time())- 하이퍼 파라미터 값 정의
RND_MEAN = 0 #정규분포 난숫값 평균
RND_STD = 0.0030 #정규분포 난숫값 표준편차
LEARNING_RATE = 0.001 #학습율- 실험용 메인 함수(report = 중간보고 주기)
def abalone_exec(epoch_count=10, mb_size=10, report=1):
load_abalone_dataset()
init_model()
train_and_test(epoch_count, mb_size, report)- 데이터셋 생성 load_abalone_dataset()
def load_abalone_dataset():
with open('.../Study/파이썬 날코딩으로 알고 짜는 딥러닝/data/abalone.csv') as csvfile:
csvreader = csv.reader(csvfile) #csv파일을 메모리로 읽음
next(csvreader, None) # 첫 행을 읽지 않고 건너뛰게 만든다
rows = []
for row in csvreader:
rows.append(row)
global data, input_cnt, output_cnt
input_cnt, output_cnt = 10, 1 # 입출력 벡터 크기를 각각 10과 1
data = np.zeros([len(rows), input_cnt+output_cnt]) # 객체들의 입출력 정보를 저장할 데이터 행렬
# 원핫인코딩
for n, row in enumerate(rows):
if row[0] == 'I': data[n, 0] = 1
if row[0] == 'M': data[n, 1] = 1
if row[0] == 'F': data[n, 2] = 1
data[n, 3:] = row[1:]- 파라미터 초기화 함수 정의 init_model()
def init_model():
global weight, bias, input_cnt, output_cnt
# 평균과 표준편차를 기준으로 input_cnt행 output_cnt열 가중치 생성 (10,1)
# 난숫값으로
weight = np.random.normal(RND_MEAN, RND_STD,[input_cnt, output_cnt])
# 편향벡터 1행1열
bias = np.zeros([output_cnt])- 학습 및 평가 함수 정의 train_and_test(epoch_count, mb_size, report)
def train_and_test(epoch_count, mb_size, report):
step_count = arrange_data(mb_size) # 데이터를 섞고 학습용/평가용 데이터셋 분리, 정렬 등
test_x, test_y = get_test_data()
for epoch in range(epoch_count): # epoch만큼 학습 반복
losses, accs = [], []
for n in range(step_count): # 값 만큼 미니배치 처리
train_x, train_y = get_train_data(mb_size, n)
loss, acc = run_train(train_x, train_y)
losses.append(loss)
accs.append(acc)
if report > 0 and (epoch+1) % report == 0: # 지정된 보고 주기에 해당하는지 검사
acc = run_test(test_x, test_y)
print('Epoch {}: loss={:5.3f}, accuracy={:5.3f}/{:5.3f}'. \
format(epoch+1, np.mean(losses), np.mean(accs), acc))
final_acc = run_test(test_x, test_y)
print('\nFinal Test: final accuracy = {:5.3f}'.format(final_acc))- 학습 및 평가 데이터 획득 함수 정의
def arrange_data(mb_size):
global data, shuffle_map, test_begin_idx
shuffle_map = np.arange(data.shape[0]) #인덱스 만들기
np.random.shuffle(shuffle_map) #인덱스 섞음
step_count = int(data.shape[0] * 0.8) // mb_size # 미니배치 학습에 필요한 배치 수
test_begin_idx = step_count * mb_size # train test 분류 경계 인덱스
return step_count
def get_test_data():
global data, shuffle_map, test_begin_idx, output_cnt
test_data = data[shuffle_map[test_begin_idx:]]
return test_data[:, :-output_cnt], test_data[:, -output_cnt:]
def get_train_data(mb_size, nth):
global data, shuffle_map, test_begin_idx, output_cnt
if nth == 0: #epoch의 첫번째 호출에 학습데이터에 대한 부분적인 순서을 뒤섞음
np.random.shuffle(shuffle_map[:test_begin_idx])
train_data = data[shuffle_map[mb_size*nth:mb_size*(nth+1)]] #미니배치 구간의 위치를 따져 그 구간에 해당하는 shuffle_map만 가져옴
return train_data[:, :-output_cnt], train_data[:, -output_cnt:]- 학습 실행 함수와 평가 실행 함수 정의
def run_train(x, y):
output, aux_nn = forward_neuralnet(x) #순전파 처리
loss, aux_pp = forward_postproc(output, y) #순전파 처리
accuracy = eval_accuracy(output, y) #정확도 계산
#aux_pp, aux_nn은 순전파 과정에서 확보 가능한 것들을 챙겨 역전파 함수에 전달
#불필요한 계산을 줄여 효율을 높임
G_loss = 1.0
G_output = backprop_postproc(G_loss, aux_pp)
backprop_neuralnet(G_output, aux_nn)
return loss, accuracy
def run_test(x, y):
output, _ = forward_neuralnet(x)
accuracy = eval_accuracy(output, y)
return accuracy가중치의 손실 기울기
-
Y = XW +B일 때 Y_ij = X_i * W_j + B_j임 즉
-
이는 곧 다음 식과 같음
-
Y_ij의 손실 기울기는
-
결국 Y_ij를 통해 미치는 부분은
-
행렬 곱샘 형식과 일치하지 않아서 전치(Transpose)시킴
-
따라서
편향의 손실 기울기
-
Y = XW +B일 때 Yij = X_i * W__j + Bj임 즉
-
결국
- 단측 퍼셉트론에 대한 순전파 및 역전파 함수 정의 (바로 위 설명 참고)
def forward_neuralnet(x):
global weight, bias
output = np.matmul(x, weight) + bias
return output, x #역전파의 보조를 위해 x도 같이 반환
def backprop_neuralnet(G_output, x): # G_output:순전파 output에 대한 손실 기울기
global weight, bias
g_output_w = x.transpose()
G_w = np.matmul(g_output_w, G_output)
G_b = np.sum(G_output, axis=0)
weight -= LEARNING_RATE * G_w
bias -= LEARNING_RATE * G_b평균제곱오차의 역전파
-
순전파는 편차 -> 제곱 -> 평균 순서로 output -> diff -> square -> loss임
-
따라서 역전파는 그 반대로 손실 기울기 1로부터 square -> diff -> output 으로 이어짐
-
평균 연산은
- 이 값을 square 텐서와 같은 구조로 모은 것이 G_loss_square임 -
제곱 연산은
-
편차 연산은
- 후처리 과정에 대한 순전파 및 역전파 함수 정의 (바로 위 설명 참고)
def forward_postproc(output, y):
diff = output - y
square = np.square(diff)
loss = np.mean(square) # 손실함수는 평균계산에 의한 함수 즉 스칼라텐서
return loss, diff
def backprop_postproc(G_loss, diff): # G_loss는 초기에 1로 설정돼있음
shape = diff.shape
g_loss_square = np.ones(shape) / np.prod(shape)
g_square_diff = 2 * diff
g_diff_output = 1
G_square = g_loss_square * G_loss
G_diff = g_square_diff * G_square
G_output = g_diff_output * G_diff
return G_output
def backprop_postproc_oneline(G_loss, diff): # backprop_postproc() 대신 사용 가능
return 2 * diff / np.prod(diff.shape)- 정확도 계산 함수 정의
def eval_accuracy(output, y):
mdiff = np.mean(np.abs((output - y)/y))
return 1 - mdiff