
✔ Summary
Task: 배달노동자를 위한 서울시 이동노동자 간이 쉼터 최적입지 선정
Tools: Python, QGIS, R
ALgoritms: MCLP (Maximal Covering Location Problem)
🤔 프로젝트 선정이유
- 최근 온라인 음식 배달 시장과, 배달업 시장의 규모가 증가하고 있음
- 배달 노동자는 지속적으로 증가하지만 배달 대기시간에 이용할 쉼터는 부족
- 현존하는 이동노동자 쉼터는 접근성이 떨어짐
- 서울시 지자체에서 이동노동자 간이쉼터 증설 계획이 있고 이에 대하여 최적입지를 제안하고자 함
📊 사용한 데이터
- 공공데이터를 수집해서 사용했으며 Raw 데이터 목록에 정리되어 있음
- 실제 분석에 사용된 데이터는 data 폴더에 정리되어 있음
👨💻 분석 내용
- EDA 및 시계열 분석을 통해 현황과, 앞으로 배달 수요 증가 추세를 확인함 -> 시계열 분석 담당
- 주성분 분석, 상관분석을 통해 사용할 변수 채택
- 군집분석(계층적, k-means, k-medoids, GMM)결과 보팅을 통해 행정구 선정
- 행정구 내 최적입지 선정을 위해 공간최적화모델(LSCP, MCLP 알고리즘) 적용, 프로젝트의 방향성에 더 적합한 MCLP 모델을 최종 모델로 채택 -> 공간최적화 분석 담당
📝 분석 결과
📈 시계열 분석
- 분석을 하기 앞서 확인한 EDA 중 하나로 시간별 배달 횟수를 확인해봄 -> 이는 이동노동자 간이쉼터 오픈 시간에 대한 인사이트를 제시할 수 있음
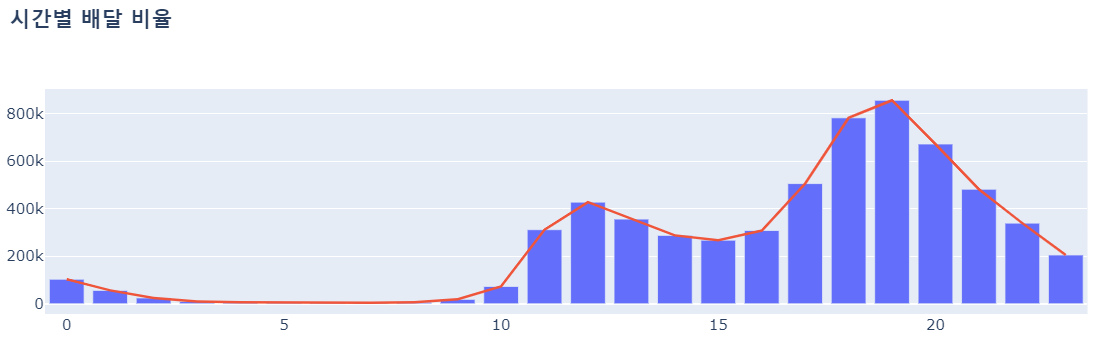
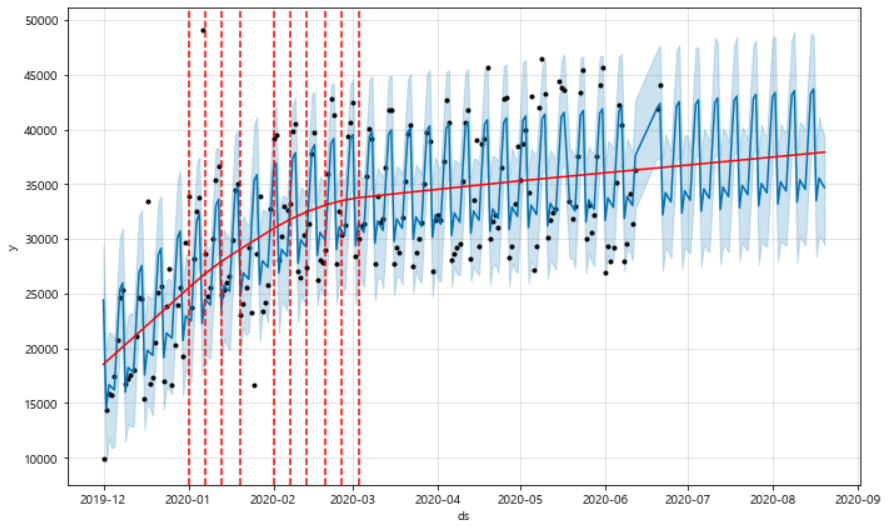
- 시계열 분석은 Facebook에서 개발은 Prophet 알고리즘을 적용하여 진행하였고, 주어진 데이터(2019.12 ~ 2020 06.20)를 기반으로 분석을 진행 했을 때 배달의 추세는 증가할 것으로 나타남 -> 본 프로젝트 필요성의 근거가 될 수 있음
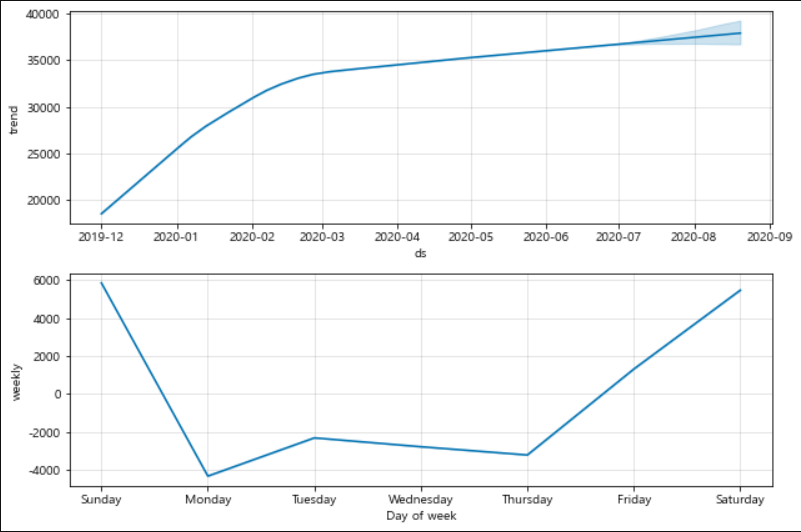
- 추가적으로 Prophet 알고리즘의 components를 통해 더 간명한 시계열 예측 그래프와 요일별 추세를 알 수 있었음 -> 이는 이동노동자 간이 쉼터가 더 관리되어야 하는 날에대한 인사이트를 줄 수 있음
📉 LSCP
- 구체적인 입지 선정에 앞서 전반적으로 한 행정구의 수요를 커버할 수 있는 쉼터의 개수(평균3개)를 탐색하기 위한 목적으로 진행함.
- 대한민국 읍면동 경계 shp 베이스로 진행했으며 정확한 결과와는 다소 거리가 있으나 탐색적인 의미이기에 참고 정도로 사용함
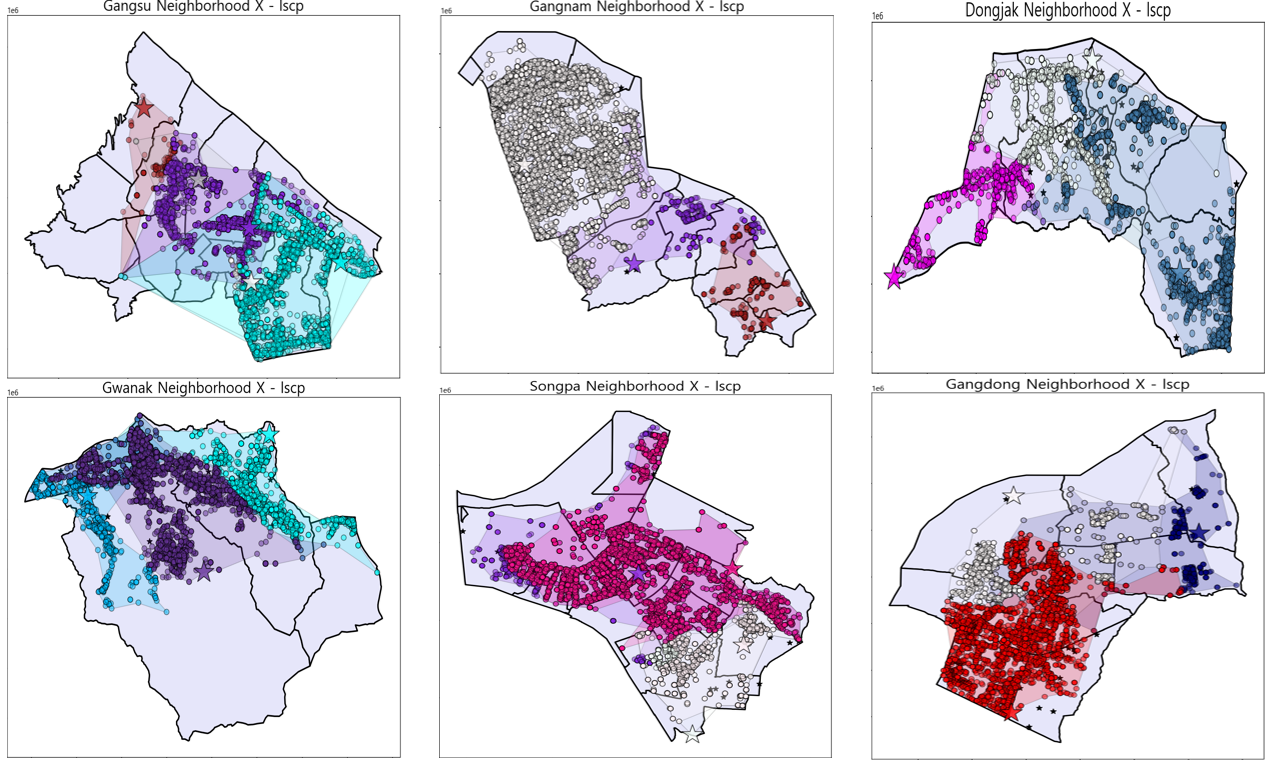
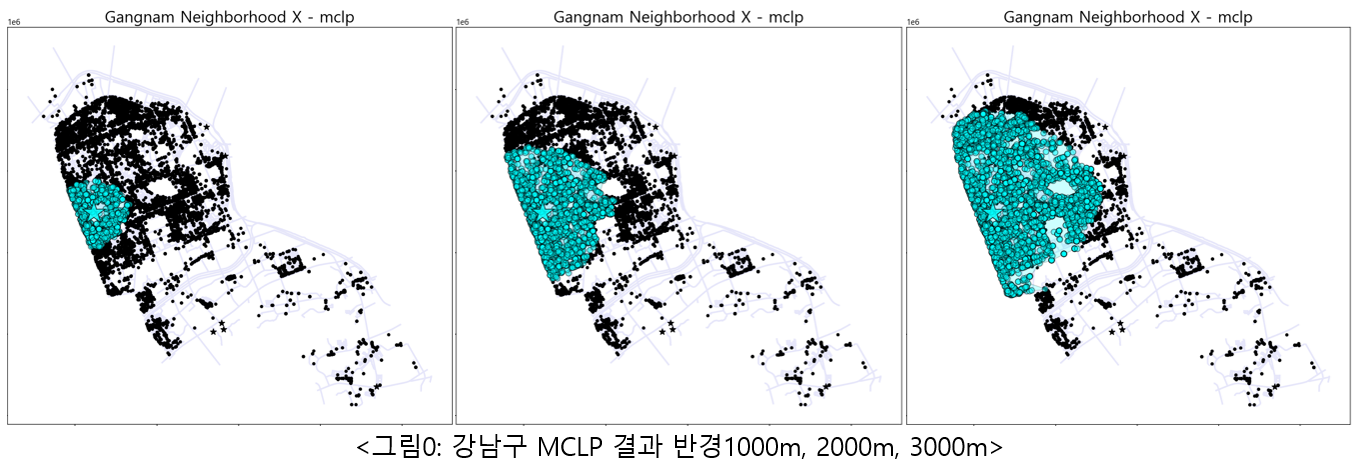
🧭 MCLP
- MCLP는 현실적인 제약사항을 고려할 수 있는 알고리즘으로, 프로젝트에 가장 적합한 알고리즘이라고 판단함
- LSCP가 약간은 탐색적인 의미라면 MCLP는 확실한 최종 입지 선정을 목적으로 진행함.
- MCLP 결과를 베이스로 최종입지를 선정함(다음 사진은 결과 일부)


🧐 개선 방향
- 공간 최적화 모델을 적용하는데 있어서, 범위를 행정구 단위로 잡으면서 범위를 조금 더 작게 잡은 상태에서 진행한다면 더 구체적이고 현실적인 결과물을 만들 수 있다고 생각함
- MCLP에 사용되는 가중치 계수에 조금 더 다양한 데이터를 반영한다면 더 최적화된 입지선정 알고리즘을 만들 수 있다고 생각함, 수집한 데이터 품질과 다양성에 대한 아쉬움이 가장 크게 남았음
😀 배운점
- 주제 선정부터 데이터 수집, 분석, 산출물 납기 까지 하나의 공공 프로젝트를 처음으로 경험해봄. 프로젝트의 주기를 처음부터 마지막까지 경험해보고 협업한 것이 가장 큰 의의
- 시계열 분석을 처음으로 진행하며 ARIMA모델 보다 훨씬 유연하고 사용자 친화적인 Prophet모델을 사용했는데, 시계열 분석에 대한 마음가짐을 더 편하게 가질 수 있었고, 앞으로 시계열 분석에 대한 더 빠른 접근이 가능해짐
- 첫번째로는 분석 최적화 모델이라는 새로운 모델을 공부할 수 있었다는 점, 두번째로는 복잡하게 짜여진 코드와 함수들을 조금씩 사용가능하게 바꿔가며 분석을 진행한 경험이 큰 자산이 됐음, 이를 통해 비슷한 케이스들을 분석에 적용할 수 있음
