[JavaScript] 백준 1450 냅색문제 (JS)

냅색문제

📚 문제 설명

N 개의 물건을 최대 C 무게만큼 들어가는 가방에 넣으려고 한다.
N개의 물건을 가방에 넣는 경우의 수를 구하여라.

물건을 담지 않는 경우도 1가지로 계산한다.

👨🏻‍💻 풀이 과정

가장 간단하게 생각해서 각각의 물건을 넣을 경우의 수를 계산한다고 하면 N은 최대 30이기 때문에 2^30 만큼 계산을 해야한다.
이런 경우 사용하는 알고리즘이 MITM (Meet In The Middle) 알고리즘이다.

💡 Meet In The Middle (MITM)

MITM 알고리즘은 간단하게 말하자면 나눠서 계산하는 것이라고 생각하면 된다.
이 문제를 예시로 들면, 만약 N개의 부분집합을 구하려면 $2^N$ 이지만,
만약 2개로 나누어서 부분집합을 구한다면 2 * $2^{\frac{N}{2}}$ 이기 때문에 속도가 훨씬 빠르다.

그 후에 하나의 집합에서 다른 집합으로 Binary Search를 이용해서 정답을 찾으면 될 것이다.

• N개의 물건을 A, B 두개의 집합으로 나눈다.
• 두 집합의 부분집합의 합을 구한다. (SumA, SumB)
• SumA를 Binary Search를 위해 정렬.
• SumB[i] + SumA[mid] 가 C 이하가 되는 값을 찾는다.
• mid를 찾으면 SumA를 정렬되었기 때문에 mid가 갯수이다. 따라서 모든 mid 값을 더하면 정답.

아래 그림은 입력이 아래와 같을 때, 계산하는 과정이다.

2 1
1 1

SumB[0] 일 때

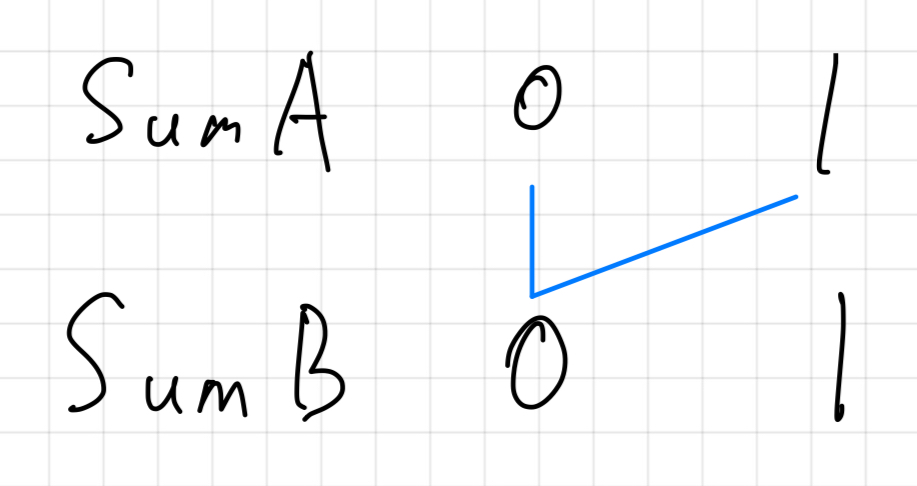
SumB[1] 일 때

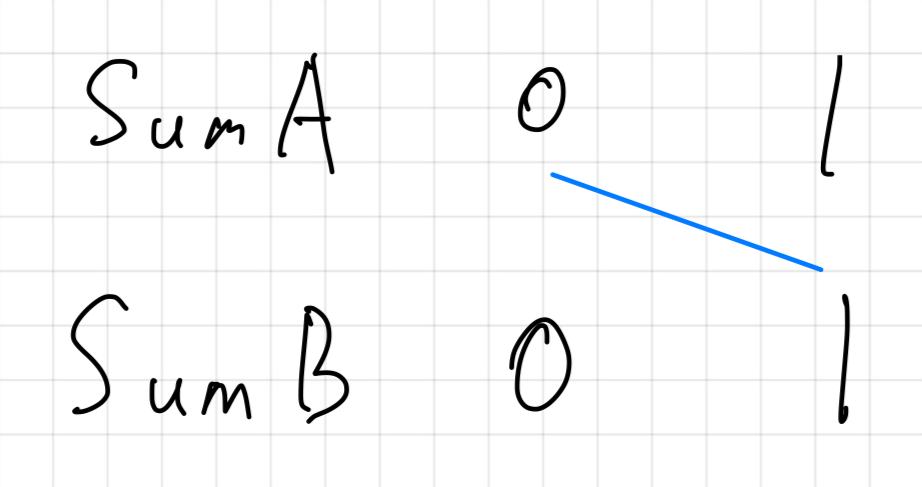
전체 코드

    let input = require("fs").readFileSync(0, 'utf-8').toString().trim().split("\n");
    const [N, C] = input[0].split(" ").map(Number);
    input = input[1].split(' ').map(Number);
	// 짐을 2개의 집합으로 나눔 (A,B)
    const A = input.splice(0, parseInt(input.length / 2));
    const B = input;
	// 부분 집합의 합을 구할 배열.
    let SumA = [];
    let SumB = [];
	// 부분 집합의 합을 찾는 함수.
	// 재귀를 이용해 구현.
    const SumSubset = (Arr, targetArr, index, sum) => {
        if (index === Arr.length) {
            targetArr.push(sum);
            return;
        }
        SumSubset(Arr, targetArr, index + 1, sum);
        SumSubset(Arr, targetArr, index + 1, sum + Arr[index]);
    };
	// 이분탐색.
    const BinarySearch = (Arr, T) => {
        let Start = 0;
        let End = Arr.length;

        while (Start < End) {
            const mid = Math.floor((Start + End) / 2);
            if (Arr[mid] <= T) {
                Start = mid + 1;
            } else {
                End = mid;
            }
        }

        return End;
    };
	// 2개의 부분집합의 합을 찾아줌.
    SumSubset(A, SumA, 0, 0);
    SumSubset(B, SumB, 0, 0);
	// 이분 탐색을 위해 정렬.
    SumA.sort((a, b) => a - b);

    let result = 0;
	// 반복문을 돌며 확인.
    for (const num of SumB) {
        if (num > C) {
            continue;
        }

        result += BinarySearch(SumA, C - num);
    }
    console.log(result);

🧐 후기

MITM 알고리즘을 처음 알게 된 문제였다. 전체적인 로직이 생각보다 복잡해서 다른분들의 코드를 보고도 이해하기가 힘들었다.
이 문제는 기본적으로 MITM 알고리즘을 이용하기 위해 집합을 나눈 후에, Binary Search를 이용해서 두 집합을 비교하는 방식으로 진행되었다.