선수과목 (Prerequisite

📚 문제 설명
1 ~ N 까지 과목이 있다. 과목 중에는 선수과목이 있는 과목이 있다.
모든 과목을 들으려고 할 때, 각 과목을 듣기 위한 최소 학기 수를 구해야 한다.
"A B" 가 입력으로 주어졌을 떄,
B를 듣기 위해서는 A를 들어야 한다는 뜻이고
1 <= A < B <= N 이다.
👨🏻💻 풀이 과정
이 문제를 푸는데 2가지 방법으로 진행했다.
- DP
- 위상 정렬
우선 선수과목 A B가 주어졌을 때,
1 <= A < B <= N 인점을 이용해 풀었던 첫번째 풀이부터 알아보자.
💡 Dynamic Programming (DP)
우선 dp[i]는 i 과목을 듣기 위한 최소 학기 수 이다.
모든 dp 배열을 1로 초기화 시켜주었다.
그 후 입력으로 받은 선수과목 A B를 A를 기준으로 정렬해 주었다.
이 후 모든 선수과목에 대해
dp[B] = Math.max(dp[B], dp[A] + 1)
하면 결과가 나올 것이다.
이 풀이는 앞에서도 말했지만, 선수과목이 A < B 조건을 가지고 있기 때문에 가능하다.
전체 풀이
let fs = require("fs");
let input = require("fs").readFileSync(0, 'utf-8').toString().trim().split("\n");
const [N, M] = input.shift().split(' ').map(Number);
// 선수과목 입력.
const Restriction = input.map(v => v.split(' ').map(Number));
// 1로 초기화한 dp배열
let dp = new Array(N).fill(1);
// 정렬.
Restriction.sort((a, b) => a[0] - b[0]);
// 점화식 dp[B] = Math.max(dp[B], dp[A] + 1) 적용.
Restriction.forEach(v => {
dp[v[1] - 1] = Math.max(dp[v[1] - 1], dp[v[0] - 1] + 1);
});
// 정답 출력.
console.log(dp.join(' '));
일단 이렇게 성공했으나, 다른 코드들에 비해 시간이 많이 나온 것을 알 수 있다.
(물론 많은 코드들이 1000ms가 넘었지만, 700ms ~ 900ms 코드도 많았다.)
따라서 내가 접근한 방식 외의 다른 방식이 있을 것이라고 생각해 찾아보니 다른 풀이의 경우 위상 정렬 알고리즘을 이용했다는 것을 알게 되었다.
💡 Topological Sort (위상 정렬)
위상 정렬 알고리즘은 순서가 있는 일에 대한 정렬을 진행할 때 사용한다.
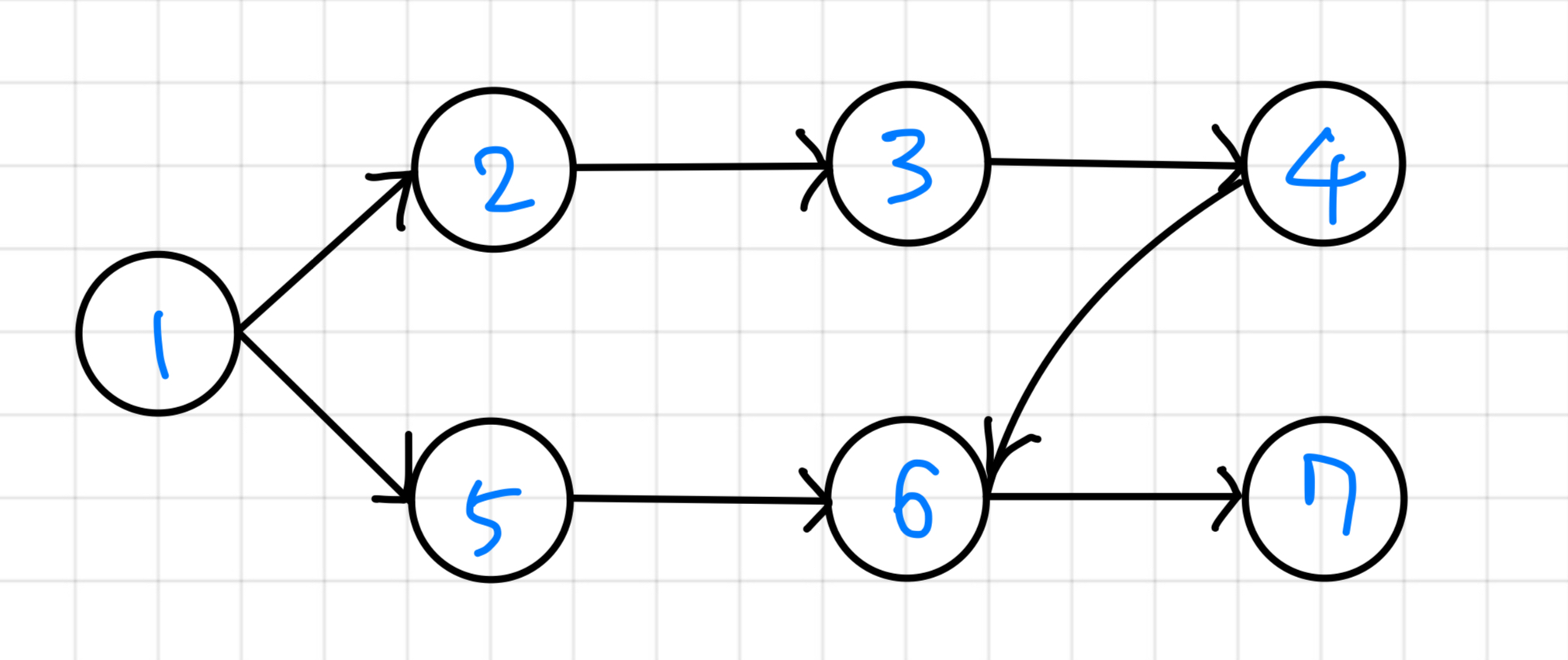
아래 그림을 예시로 들어보자.
화살표가 선수과목을 의미한다고 했을 때, 6의 경우 5와 4를 들어야 들을 수 있다.
따라서 정렬을 진행하면 다음과 같이 정렬되어야 한다.
1 - 2 - 5 - 3 - 4 - 6 - 7
그럼 위상 정렬을 어떻게 구현할지 생각해보자.
- 들어오는 간선이 0인 노드부터 확인.
- 간선을 지워주면서 확인.
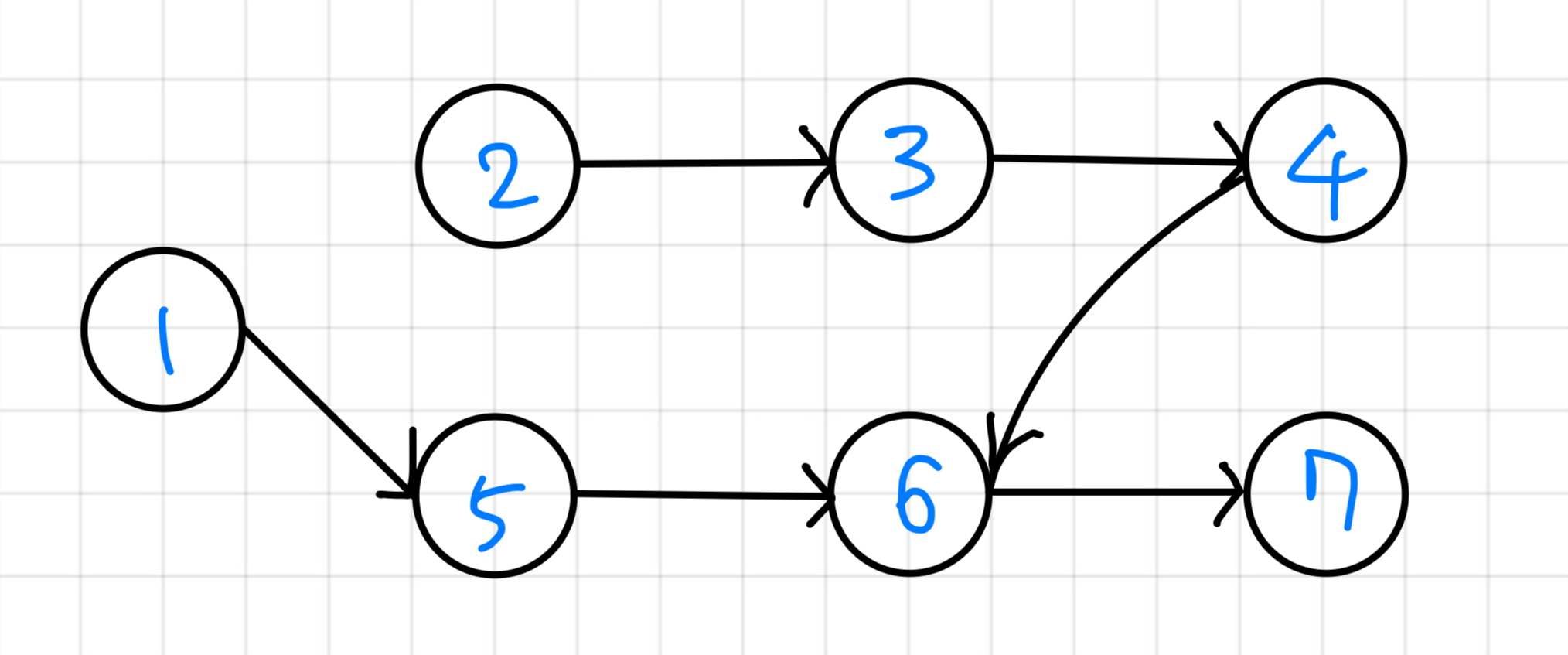
들어오는 간선이 0개인 1부터 큐에 삽입
| Queue | 1 |
|---|

Now === 1
| Queue | 2 |
|---|---|
| 확인 순서 | 1 |
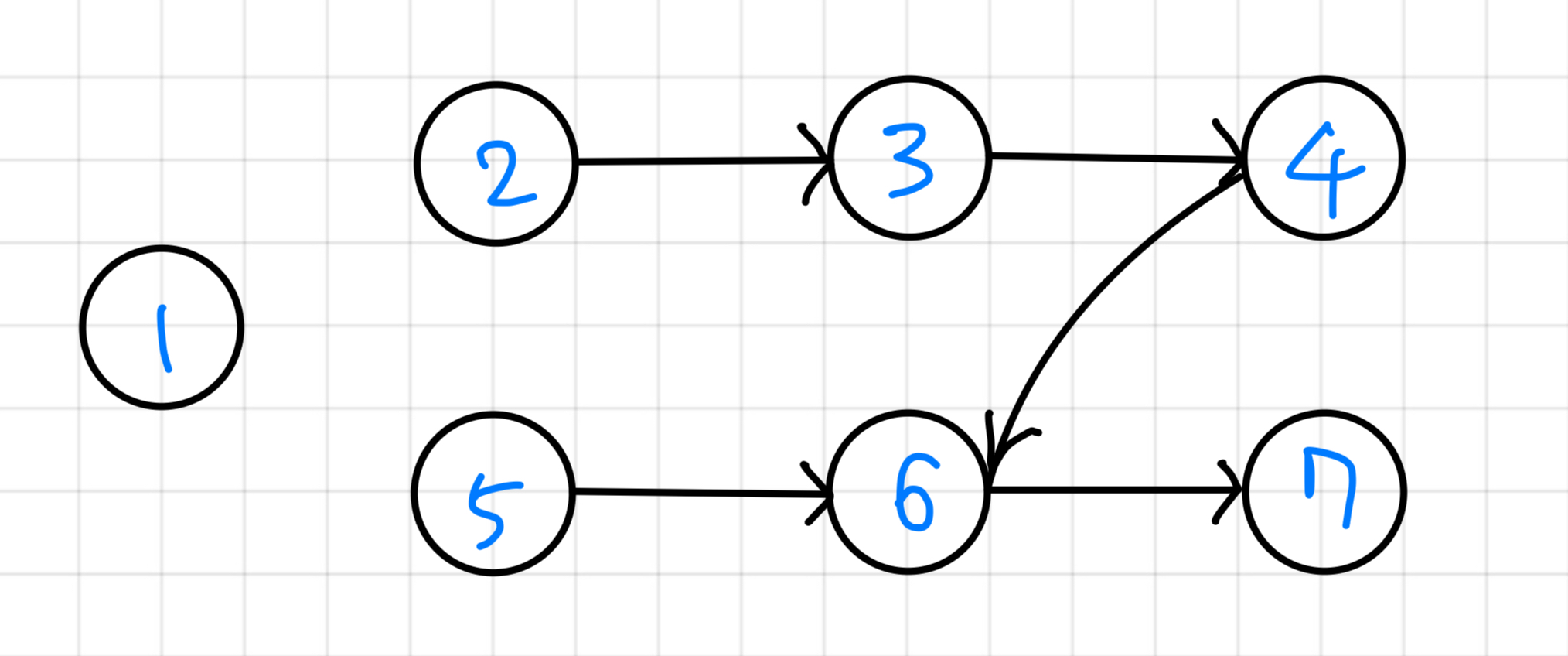
Now === 1
| Queue | 2 | 5 |
|---|---|---|
| 확인 순서 | 1 |
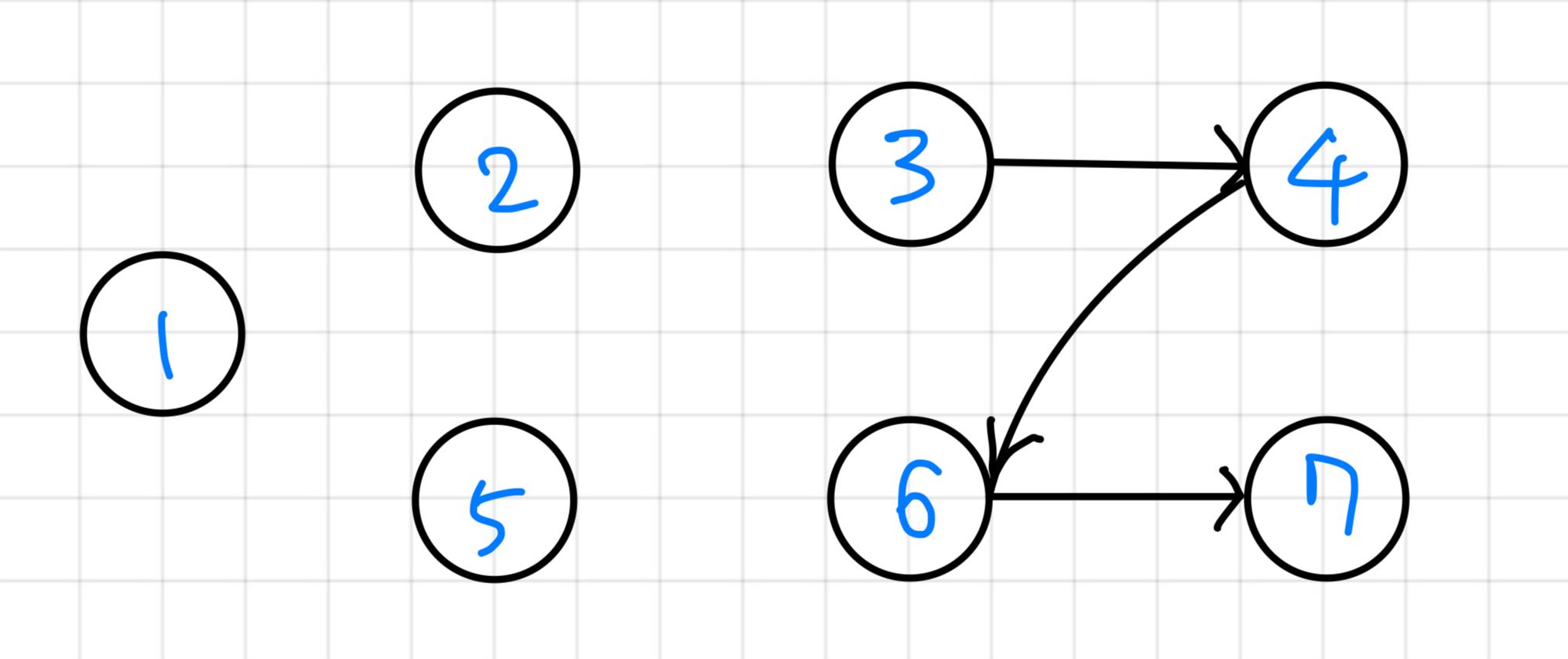
(빠른 설명을 위해 2와 5를 함꼐 설명)
(실재 코드에서는 2, 5 각각 진행)
Now === 2, 5
| Queue | 3 | ||
|---|---|---|---|
| 확인 순서 | 1 | 2 | 5 |
Now === 3
| Queue | 4 | |||
|---|---|---|---|---|
| 확인 순서 | 1 | 2 | 5 | 3 |
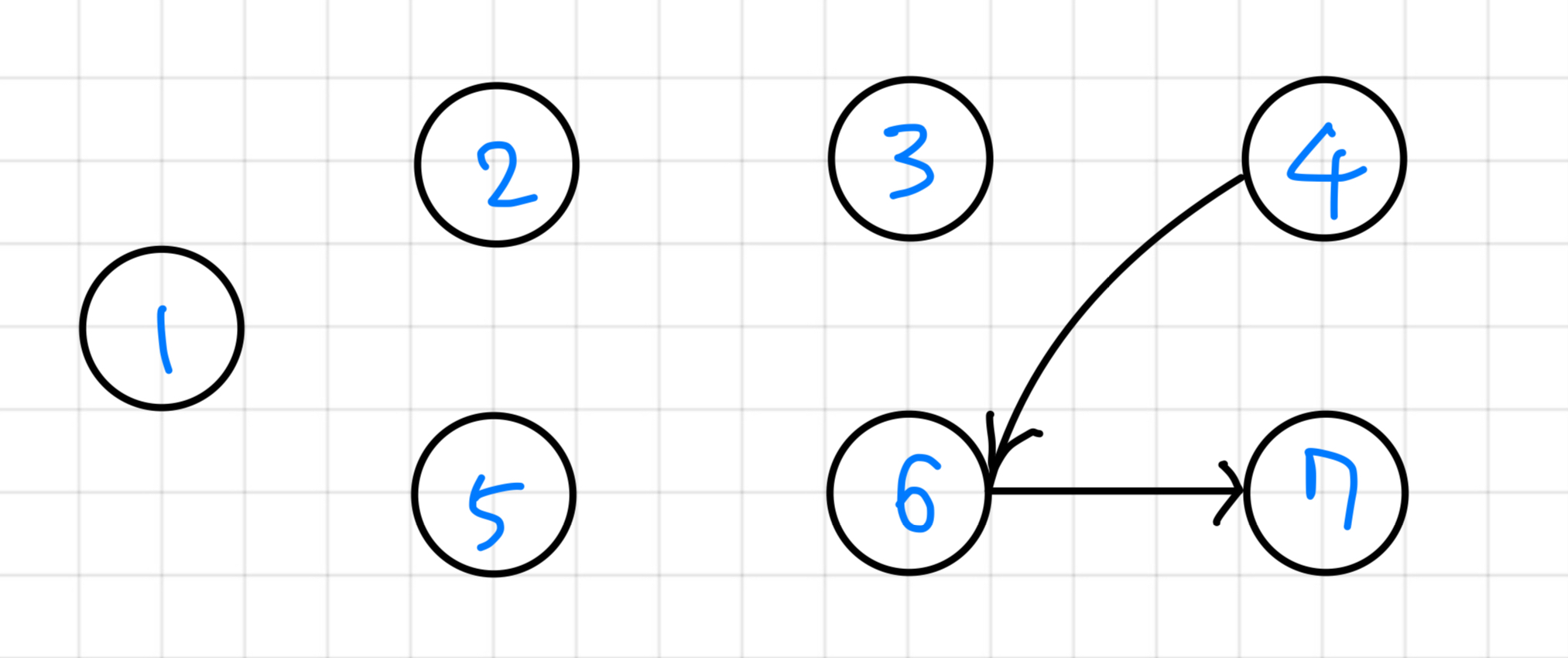
Now === 4
| Queue | 6 | ||||
|---|---|---|---|---|---|
| 확인 순서 | 1 | 2 | 5 | 3 | 4 |
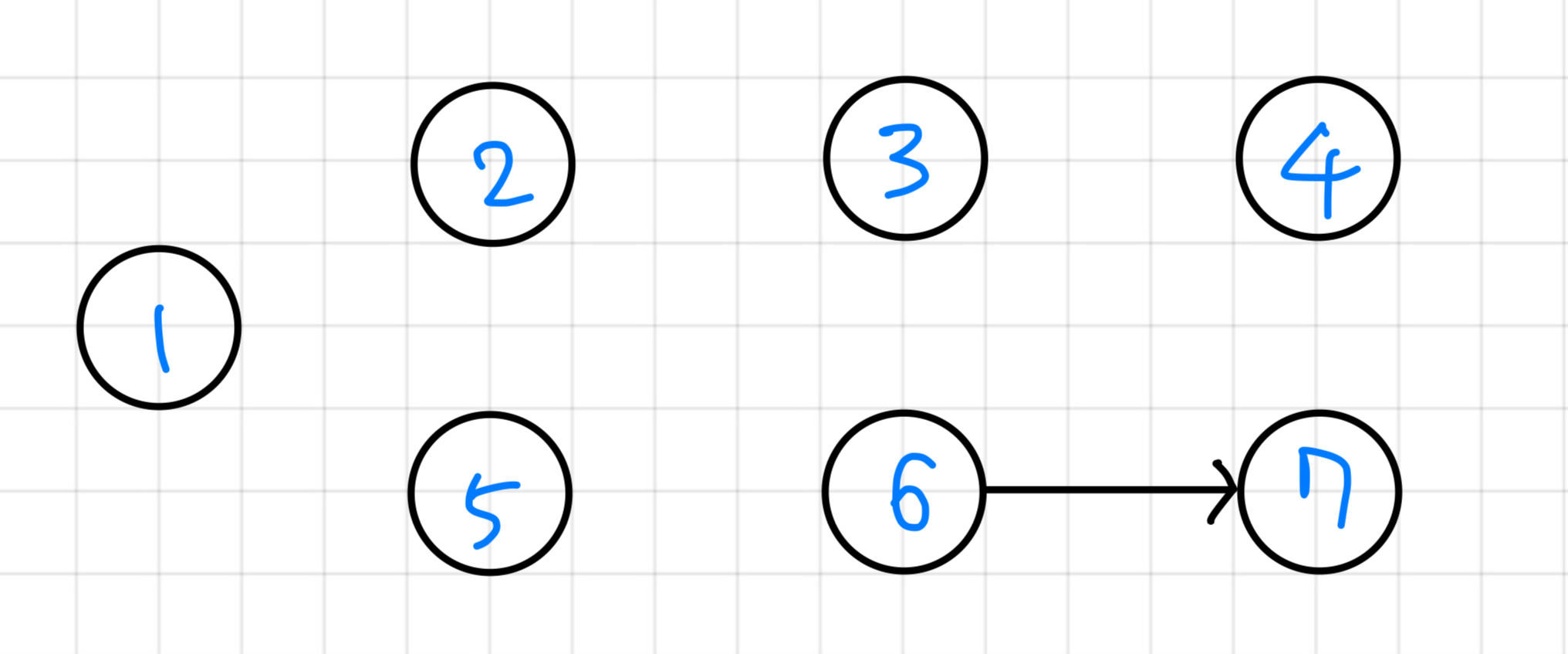
Now === 6
| Queue | 7 | |||||
|---|---|---|---|---|---|---|
| 확인 순서 | 1 | 2 | 5 | 3 | 4 | 6 |
이렇게 진행 되어 최종적으로 Queue가 빌 때까지 진행하면
확인 순서는 1 - 2 - 5 - 3 - 4 - 6 - 7 이 된다.
참고로 위상 정렬의 경우 DAG에서만 가능하며 만약 회전하는 형식으로 되어있다면 사용하면 안된다.
예를 들어 7 -> 1 이라면 무한히 돌게 될 것이다.
그럼 이제 코드로 구현해보자.
우선 위상 정렬을 진행하기 전에 가장 처음 확인할 노드는 자신에게 들어오는 간선이 없는 노드들부터 계산해야 한다.
따라서 count 배열을 이용해 각각의 노드에 들어오는 간선의 갯수를 저장했다.
count 배열 / 연결 관계 저장
// 연결 관계 저장.
let lines = {};
// 들어오는 간선의 갯수.
let count = new Array(N + 1).fill(0);
// 초기화.
for (let i = 1; i < N + 1; i++) {
lines[i] = [];
}
// 입력에 맞춰 lines, count 갱신.
input.forEach(v => {
const [Start, End] = v.split(' ').map(Number);
lines[Start].push(End);
count[End]++;
});이렇게 변수를 저장한 후에는 생각보다 간단하다.
우리가 하고 싶은건 아래와 같고 이렇게 나열해보면 우리가 익숙한 BFS와 유사하게 구현할 수 있다는 생각을 할 수 있다.
- 들어오는 간선이 0 인 값들을 Queue에 삽입.
Queue에서 하나씩 확인하여lines을 통해 연결된 노드를 확인.count가 0인 노드를 지날 경우 해당 노드를Queue에 삽입.
전체 코드
let fs = require("fs");
let input = require("fs").readFileSync(0, 'utf-8').toString().trim().split("\n");
const [N, M] = input.shift().split(' ').map(Number);
let answer = new Array(N).fill(0);
// 연결 관계 저장.
let lines = {};
// 들어오는 간선의 갯수.
let count = new Array(N + 1).fill(0);
// 초기화.
for (let i = 1; i < N + 1; i++) {
lines[i] = [];
}
// 입력에 맞춰 lines, count 갱신.
input.forEach(v => {
const [Start, End] = v.split(' ').map(Number);
lines[Start].push(End);
count[End]++;
});
// 위상 정렬 코드
const TopologicalSort = () => {
let Queue = [];
// 들어오는 간선이 0인 노드들만 큐에 삽입.
for (let i = 1; i < count.length; i++) {
if (count[i] === 0) {
Queue.push([i, 1]);
}
}
let idx = 0;
// BFS와 유사한 while문 이용.
while (Queue.length > idx) {
const [now, time] = Queue[idx];
// 정답 배열 갱신.
answer[now - 1] = time;
for (const next of lines[now]) {
// 간선 제거.
count[next]--;
// 만약 들어오는 간선이 0개라면 큐에 삽입.
if (count[next] === 0) {
Queue.push([next, time + 1]);
}
}
idx++;
}
console.log(answer.join(' '));
};
TopologicalSort();
이렇게 제출하면 통과하게 되고 확실하게 시간이 줄어든 것을 확인할 수 있다.
(런타임 에러는 입력 주소를 실수해서 나왔다.)
🧐 후기
위상 정렬을 처음 보게 되어 위상 정렬에 대해 이해하느라 오래 걸렸던 문제였다.
결국 위상 정렬은 들어오는 간선의 갯수를 카운트해주는 count 변수를 만들기만 하면 BFS와 똑같다고 생각이 들었다.
