수 찾기

문제 설명
입력으로 N개의 숫자 가 랜덤하게 주어진다 그리고 M개의 숫자가 랜덤으로 주어지고 뒤에 주어진 M개의 숫자를 순서대로
N개의 숫자에 있으면 1을 리턴 없으면 0을 리턴해주는 문제이다.
풀이 과정
해당 문제를 보고 우선 가장 간단하게 includes() 함수를 사용하여 반복문을 사용해 풀어보았다.
처음 코드
let fs = require("fs");
let input = fs.readFileSync("/dev/stdin").toString().trim().split("\n");
let N = parseInt(input.shift());
let answer = input.shift().split(' ').map(Number);
let M = parseInt(input.shift());
input = input.shift().split(' ').map(Number);
let Output = '';
for(let i = 0; i < M; i++){
if(answer.includes(input[i])){
Output += `1\n`;
}else{
Output += `0\n`;
}
}
console.log(Output);그런데 위의 코드는 아래에 보면 알 수 있듯 시간 초과가 발생한다.

왜 시간초과가 발생하는지 생각을 하던 중 includes()의 시간 복잡도를 알아본 결과 O(n)의 시간이 걸린다는 것을 알게 되었고
이와 유사한 Set 함수에 있는 has()는 O(1)이 걸린다는 사실 또한 알게 되었다.
왜 그럴까?
이유를 찾던 중 Hash Table(해쉬 테이블)에 대해 보게 되었다.
Hash Table(해쉬 테이블)
해쉬 테이블은 값을 저장할 때 (Key, Value)로 데이터를 저장하는 자료 구조 중 하나로
값에 대한 키값을 해쉬 함수가 계산을 하여 인덱스로 사용하는 것이다.
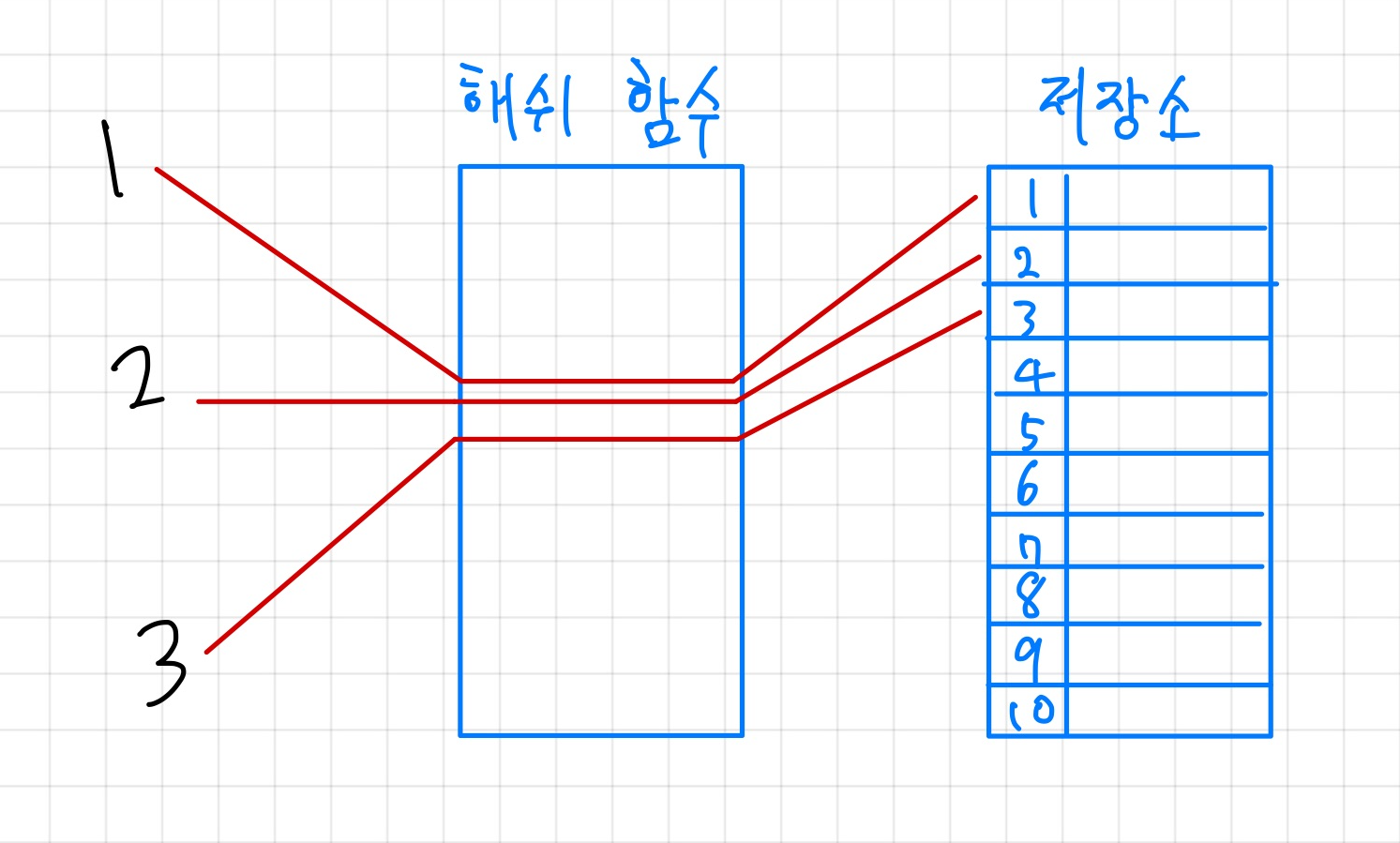
위의 그림을 예시로 들면 1을 해쉬 테이블에 저장하고자 하고 해쉬 함수가 해당 값을 그대로 내보낸다고 가정했을 때 다음과 같다.
- 1을 해쉬 함수에 넣어서 1이라는 값이 똑같이 나오게 된다.
- 해쉬 함수에서 나온 값을 키값으로 하는 위치에 저장을 한다.
따라서 해쉬 테이블을 이용하면 저장,조회,삭제 속도가 매우 빠르다.
각각의 데이터는 자신의 고유한 값을 주는 해쉬 함수에 의해 자신만의 위치에 저장이 된다.
따라서 특정 값 n을 조회한다고 했을 때 해당 값을 해쉬 함수에 넣어서 나온 값의 위치에 저장이 되어 있기 때문에
저장, 조회, 삭제의 속도가 평균적드올 O(1)로 매우 빠른편이다.
그렇다면 해쉬 테이블은 어떤 점을 주의 해야할까.
우선 이미 만들어진 저장소의 특정 Index에 해당 값을 저장하는 방식이기 때문에 공간 복잡도가 매우 높다.
그리고 두 개의 값을 저장하는데, 만약 두 값 모두 해쉬 함수에서 같은 값을 주게 되면 두 값 모두 같은 저장소에 저장을 해야 하는 문제가 생기는데 이러한 문제를 해시 충동(Hash Collision)이라고 말한다.
앞서 말한 이런 문제가 발생할 수 있기 때문에, 그리고 해쉬 함수를 이용하는 이러한 방식 때문에 자연스럽게도 해쉬 함수에 대한 의존도가 높다.
이런 해시 충돌과 같은 문제를 해결하기 위한 여러가지 방법 또한 있지만, 그건 이제 말하지 않겠다.
그럼 이제 여기서 JavaScript의 Set이 해쉬 테이블인가? 라고 묻는 다면 그것은 아니다.
Set의 구조는 인터넷 엔진(Safari, chrome 등등)에서 Data Structure를 어떻게 만들었는지에 따라 다르다고 한다.
그럼 여기서 왜 이렇게 장황하게 Hash Table에 대해 설명 했는가 묻는다면,
우리는 Set의 has() 의 시간 복잡도가 O(1) 인점을 이용하여 Hash Table과 유사하게 만들어서 사용할 수 있다는 이야기이다.
Set.has()를 이용한 풀이
let fs = require("fs");
let input = fs.readFileSync("/dev/stdin").toString().trim().split("\n");
let N = parseInt(input.shift());
let CorrectSheet = input.shift().split(' ').map(Number).sort((a, b) => a - b);
let M = parseInt(input.shift());
input = input.shift().split(' ').map(Number);
let answer = '';
CorrectSheet = new Set([...CorrectSheet]);
for (let i = 0; i < M; i++) {
if (CorrectSheet.has(input[i])) {
answer += `1\n`;
} else {
answer += `0\n`;
}
}
console.log(answer);이렇게 해서 문제를 풀게 되었다.
그렇게 문제의 알고리즘 분류를 보았는데 해당 문제는 이분 탐색 문제였다.

따라서 문제를 다시 풀게 되었다.
이분 탐색(Binary Search)을 이용한 풀이
let fs = require("fs");
let input = fs.readFileSync("/dev/stdin").toString().trim().split("\n");
let N = parseInt(input.shift());
let CorrectSheet = input.shift().split(' ').map(Number).sort((a, b) => a - b);
let M = parseInt(input.shift());
input = input.shift().split(' ').map(Number);
let answer = '';
function BinarySearch(item) {
let start = 0;
let end = CorrectSheet.length - 1;
while (start <= end) {
const mid = Math.floor((start + end) / 2);
if (item > CorrectSheet[mid]) {
start = mid + 1;
} else if (item < CorrectSheet[mid]) {
end = mid - 1;
} else {
// 아이템이 중간에 발견됨
return 1;
}
}
return 0;
}
for (let i = 0; i < input.length; i++) {
answer += `${BinarySearch(input[i])}\n`;
}
console.log(answer);후기
includes()를 이용한 풀이에서 시간초과가 나게 되어서 문제의 의도와는 다르게 Set과 has() 그리고 Hash Table까지 공부를 하게 되는 좋은 시간을 갖게 되었다.
처음에는 조사를 하며 JavaScript의 Set이나 Map이 해쉬 테이블을 사용한다는 말인줄 알았다가 자료를 조사하다가 결국 해쉬 테이블을 사용하는지는 인터넷 엔진에 따라 다르며, 원리 자체는 해쉬 테이블을 이용하여 구현하지 않았고 단순히 사람들이 Set.has()의 시간 복잡도가 O(1)인 점을 이용해 비슷하게 사용하고 있다라는 사실 또한 확실히 알게 되었따.
