[Algorithm] 15. Dynamic Programming Patterns

15. Dynamic Programming Patterns

Fibonacci

function fibonacci(n: number) {
  let a = 0,
    b = 1,
    c = 0;

  for (let i = 0; i < n; i++) {
    a = b;
    b = c;
    c = a + b;
  }

  return b;
}

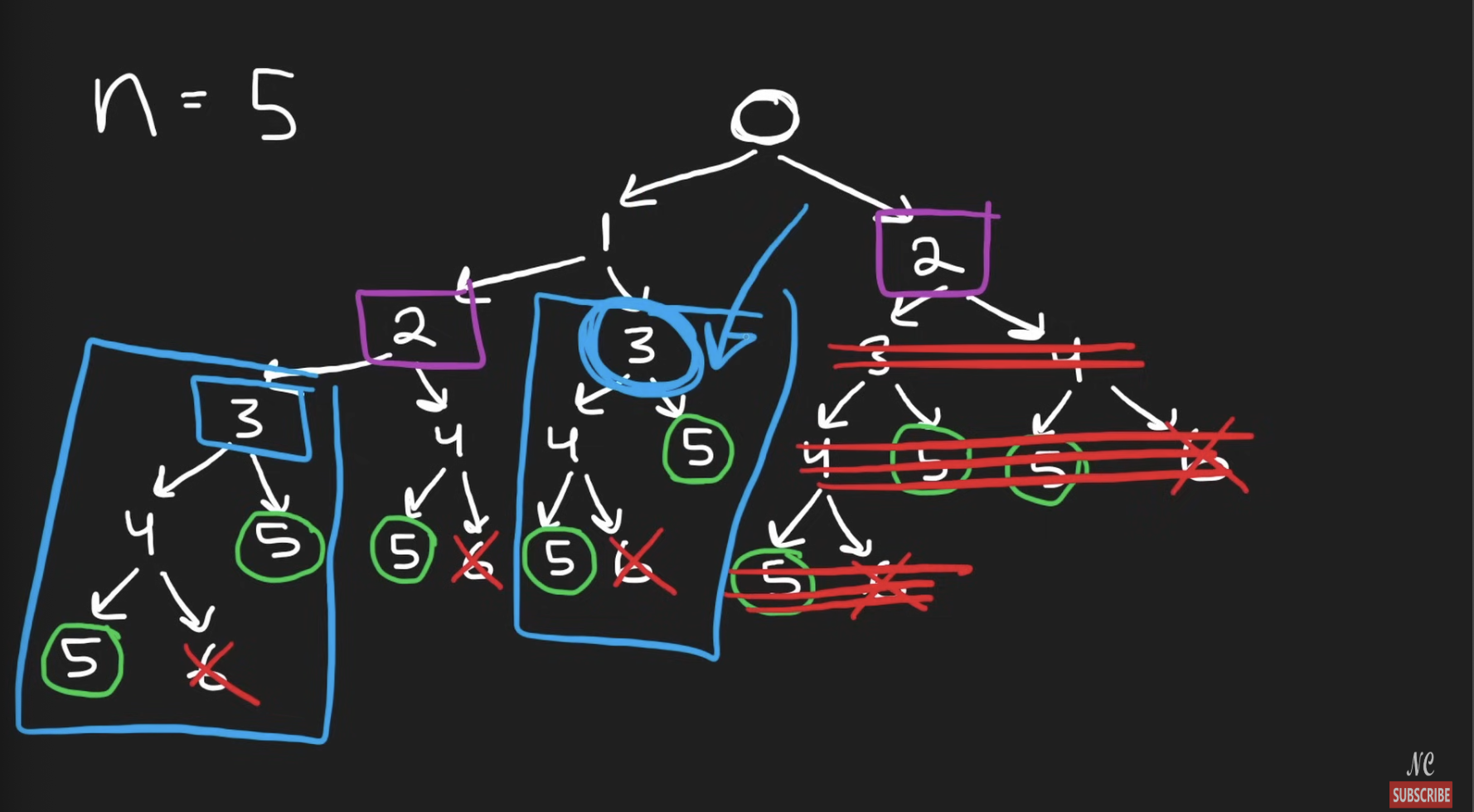
1. Climbing Stairs (LeetCode #70)

Youtube-explanation

Find a same part and do memoization(cache)

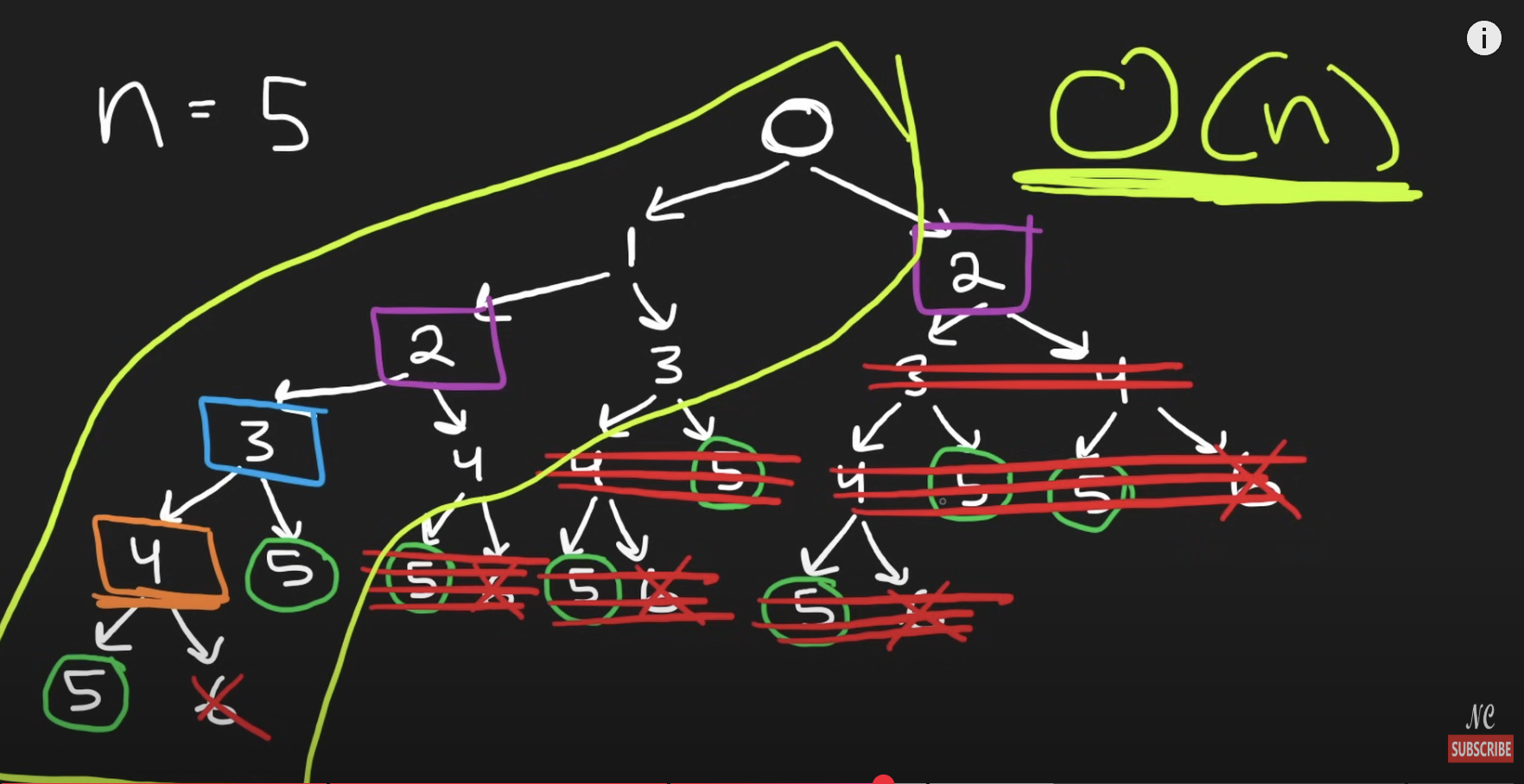
// TOP - DOWN WITH Memoization
helper(5)
├─ helper(4)
│ ├─ helper(3)
│ │ ├─ helper(2)
│ │ │ ├─ helper(1)
│ │ │ └─ helper(0)
│ │ └─ helper(1)
│ └─ helper(2) ← 여기서 이미 memo[2]가 계산되어 있음
└─ helper(3) ← 여기서도 memo[3] 사용
helper(i - 1)이 선행되며, 필요한 모든 i - k 결과들을 미리 메모이제이션 함
그 결과, helper(i - 2)는 이미 계산된 결과를 재사용
이것이 Top-Down with Memoization의 핵심

// TOP - DOWN WITH Memoization
export function climbStairsMemo(n: number): number {
  if (n <= 1) return 1;

  const memo: number[] = Array(n + 1).fill(-1);

  function helper(i: number) {
    if (i <= 2) return i; // Base case: if n is 1 or 2, return n directly

    if (memo[i] !== -1) {
      return memo[i];
    }

    memo[i] = helper(i - 1) + helper(i - 2);

    return memo[i];
  }

  return helper(n);
}

//  Bottom-Up
function climbStairs(n) {
  if (n <= 1) return 1;

  const dp = new Array(n + 1);
  dp[0] = 1;
  dp[1] = 1;

  for (let i = 2; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2];
  }

  return dp[n];
}

Simpler version : Space(1)

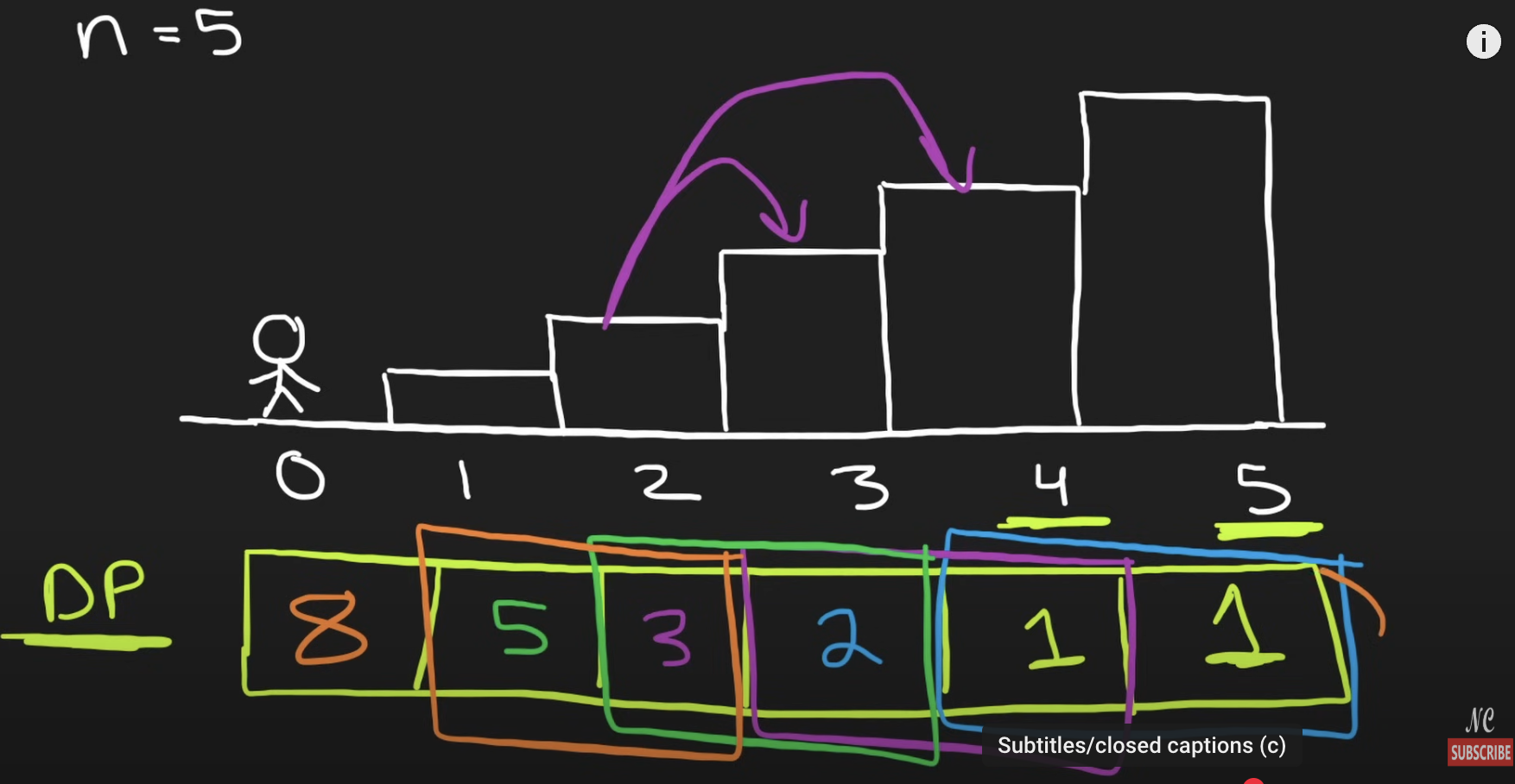
// dp like Memoization = cached
// dp: Bottom-up
// Space Optimization
function climbStairs(n: number): number {
  let one = 1,
    two = 1;
  for (let i = 0; i < n - 1; i++) {
    let temp = one;
    one = one + two;
    two = temp;
  }
  return one;
}

2. House Robber (LeetCode #198)

Youtube-explanation

function rob(nums: number[]): number {
  let rob1 = 0,
    rob2 = 0;

  // [rob1, rob2, n, n+1 ,...]
  for (const money of nums) {
    let newMaxRob = Math.max(money + rob1, rob2);
    rob1 = rob2;
    rob2 = newMaxRob;
  }

  return rob2;
}

3. Coin Change (LeetCode #322)

input : [1,2,5]
amount : 11

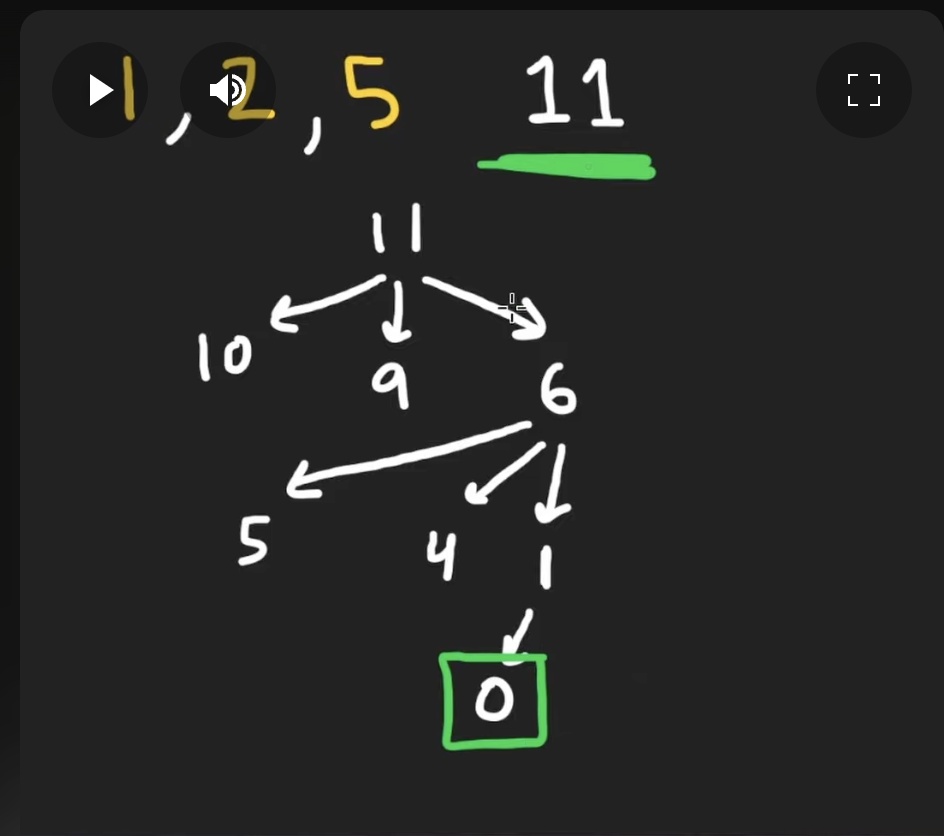
DP

// DP (bottom-up)
function coinChange(coins: number[], amount: number): number {
    const dp: number[] = new Array(amount + 1).fill(Infinity);

    dp[0] = 0;

    for(const coin of coins){
        for(let money = coin; money <= amount; money++){
            dp[money] = Math.min(dp[money], dp[money - coin] + 1);
        }
    }

    return dp[amount] === Infinity ? -1 : dp[amount]
}

BFS

// BFS
function coinChange(coins: number[], amount: number): number {
    if(amount === 0) return 0;
    const queue : number[] = [amount] ; 
    const visited : Set<number> = new Set();
    let numberOfCoins = 0;


    while(queue.length > 0){

        let size = queue.length; 
        numberOfCoins++; 


        while(size > 0){
            size--;
            const remaining = queue.shift()!;
            for(const coin of coins){
                const newRemaining = remaining - coin;
                if(newRemaining === 0) return numberOfCoins;

                if(newRemaining > 0 && !visited.has(newRemaining)){
                    visited.add(newRemaining);
                    queue.push(newRemaining);
                }
            }
        }
    }
    return -1;
};

4. Longest Common Subsequence (LCS) (LeetCode #1143)

// bottom-up DP = Top Down DP (Memoization)
// Time: O(m n)
// Space: O(m n)
// from end of string to start of string

export function longestCommonSubsequence(text1: string, text2: string): number {
  const m = text1.length,
    n = text2.length;
  const dp: number[][] = Array.from({ length: m + 1 }, () =>
    Array(n + 1).fill(0)
  );

  for (let i = m - 1; i >= 0; i--) {
    for (let j = n - 1; j >= 0; j--) {
      if (text1[i] === text2[j]) {
        dp[i][j] = 1 + dp[i + 1][j + 1];
      } else {
        dp[i][j] = Math.max(dp[i][j + 1], dp[i + 1][j]);
      }
    }
  }

  return dp[0][0];
}

// from start of string to end of string

export function longestCommonSubsequence2(
  text1: string,
  text2: string
): number {
  const m = text1.length,
    n = text2.length;

  const memo = Array.from({ length: m }, () => Array(n).fill(-1));

  function longest(i: number, j: number): number {
    if (i === m || j === n) return 0;

    if (memo[i][j] !== -1) return memo[i][j];
    if (text1[i] === text2[j]) {
      return (memo[i][j] = 1 + longest(i + 1, j + 1));
    }

    return (memo[i][j] = Math.max(longest(i, j + 1), longest(i + 1, j)));
  }

  return longest(0, 0);
}

Without DP Memoization

// Time Limit Exceeded
export function longestCommonSubsequenceTLE(
  text1: string,
  text2: string
): number {
  let m = text1.length,
    n = text2.length;

  function longest(i: number, j: number): number {
    if (i === m || j === n) return 0;

    if (text1[i] === text2[j]) return 1 + longest(i + 1, j + 1);

    return Math.max(longest(i, j + 1), longest(i + 1, j));
  }

  return longest(0, 0);
}

5. Longest Increasing Subsequence (LIS) (LeetCode #322)

// 1 Top-down
// 2 Bottom-up
// 3 Binary Search

/**
 * Complexity
Time complexity:

topDownSolution: O(n2) (due to recursive calls and memoization)
bottomUpSolution: O(n2) (nested loops for each pair of elements)
binarySearchSolution: O(nlogn) (binary search for each element)

Space complexity:

topDownSolution: O(n) (for the memo array and recursion stack)
bottomUpSolution: O(n) (for the memo array)
binarySearchSolution: O(l), where l is the length of the LIS (in the worst case, l=n)

**/
export function lengthOfLIS(nums: number[]): number {
  return topDownSolution(nums);
  // return bottomUpSolution(nums);
  // return binarySearchSolution(nums);
}

// TLE(Time Limit Exceeded)
const binarySearchSolution = (nums: number[]): number => {
  const memo: number[] = [];
  for (const num of nums) {
    let left = 0,
      right = memo.length;

    while (left < right) {
      const mid = Math.floor((left + right) / 2);

      if (memo[mid] < num) {
        console.log(memo, mid, left, right);
        left = mid + 1;
      } else {
        right = mid;
      }
    }

    if (left < memo.length) {
      memo[left] = num;
    } else {
      memo.push(num);
    }
  }

  return memo.length;
};

const bottomUpSolution = (nums: number[]): number => {
  const memo: number[] = [];

  let max = 1;

  memo[nums.length - 1] = 1;

  for (let right = nums.length - 2; right >= 0; right--) {
    let maxSequence = 0;
    for (let left = right; left < nums.length; left++) {
      if (nums[right] < nums[left]) {
        maxSequence = Math.max(maxSequence, memo[left]);
      }

      memo[right] = 1 + maxSequence;
      max = Math.max(max, memo[right]);
    }
  }

  return max;
};

const topDownSolution = (nums: number[]): number => {
  const memo: number[] = [];

  function LISByIndex(index: number): number {
    if (!memo[index]) {
      let maxSize = 1;
      for (let i = index + 1; i < nums.length; i++) {
        if (nums[index] < nums[i]) {
          const size = 1 + LISByIndex(i);
          maxSize = Math.max(maxSize, size);
        }
      }
      memo[index] = maxSize;
    }

    return memo[index];
  }

  let maxSize = 0;

  for (let i = 0; i < nums.length; i++) {
    const size = LISByIndex(i);
    maxSize = Math.max(maxSize, size);
  }

  return maxSize;
};

6. Partition Equal Subset Sum (LeetCode #416)