[Algorithm] 7.Top ‘K’ Elements

7.Top ‘K’ Elements With Heap

Why using heap?

To find largest or smallest element or stream of data using heaps or sorting.

find kth element => heap[0] element is largest or smallest
heap.pop() k time would find kth largest or smallest element.

[3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5]
-> [9, 6, 4, 5, 5,3, 2, 1, 1, 3,3] //_**not like sorted **_

         9
      /    \
     6      4
    / \    / \
   5   5  3   2
  / \    /
 1   1  3
 /
5

*heap?

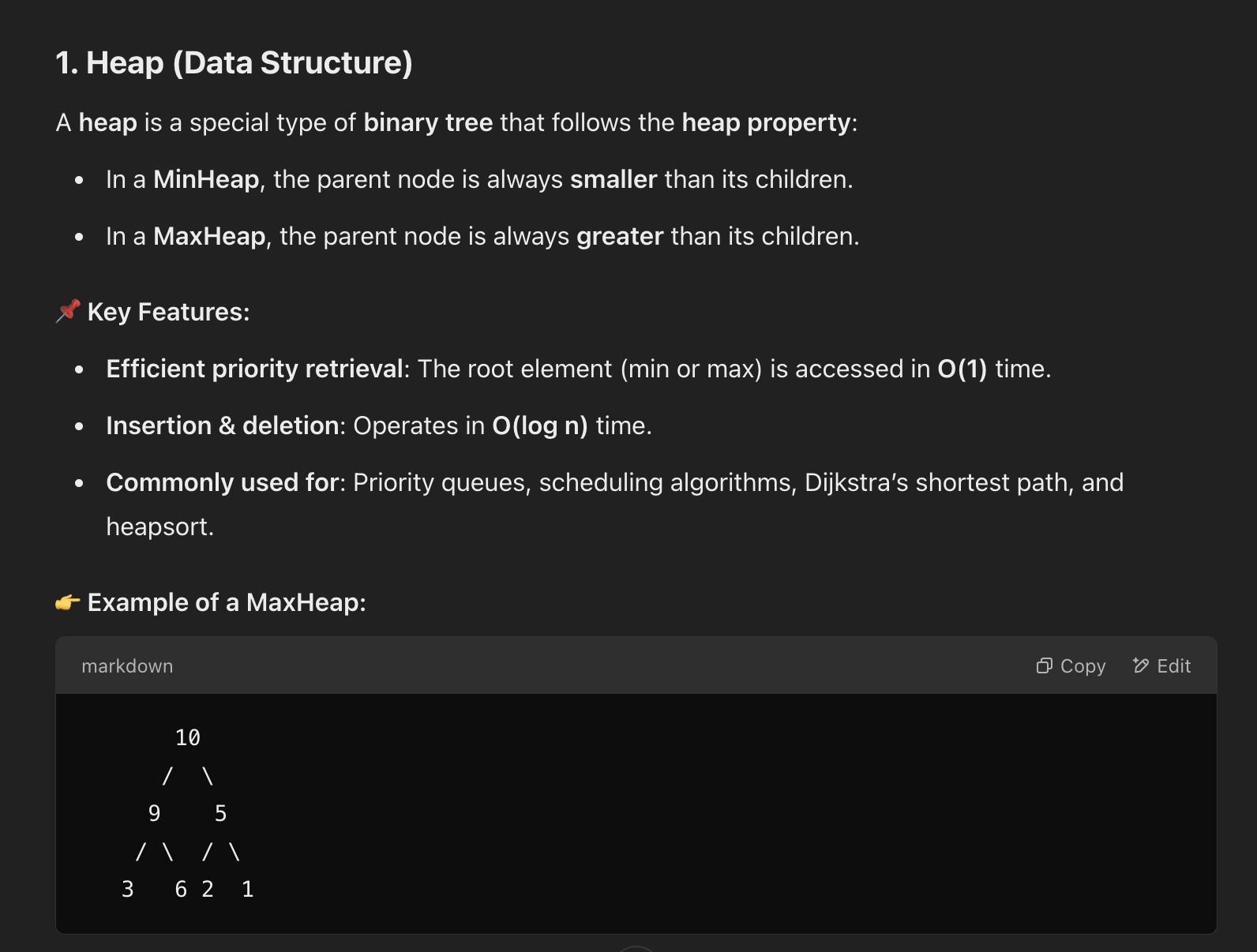
Finding a index of Parent or Child node

1. parent to child
   left child index : parentIdx x 2 + 1
   right child index : parentIdx x 2 + 2

2. child to parent
   parent index : Math.floor((childIndex - 1) / 2)

Time Complexity of JavaScript sort():

Best Case (already sorted array):

Timsort: O(n)
QuickSort (if used): O(n log n)
Average Case (random array):

Timsort: O(n log n)
QuickSort (if used): O(n log n)
Worst Case (reverse sorted or difficult cases):

Timsort: O(n log n)
QuickSort (if used): O(n^2)

1. Kth Largest Element in an Array (LeetCode #215)

Using min-heap

function findKthLargest(nums: number[], k: number): number {
    const heap = nums.slice(0, k);

    // min-heap
    function heapify (_heap: number[], idx: number) {
        let minIdx = idx; 
        const left = 2 * idx + 1; 
        const right = 2 * idx + 2; 
        if(left < _heap.length && _heap[left] < _heap[minIdx]){
            minIdx = left; 
        }
        if(right < _heap.length && _heap[right] < _heap[minIdx]){
            minIdx = right;
        }
        if(minIdx !== idx){
            [_heap[idx] , _heap[minIdx]] = [_heap[minIdx], _heap[idx]] 
            heapify(_heap, minIdx)
        }
    }

    // buildMinHeap(heap) 
    for(let i = Math.floor(heap.length / 2) ; i>= 0 ;  i-- ){
        heapify(heap, i);
    }

    //go through rest of the items
    for (let i=k; i< nums.length; i++) {
        if (nums[i] > heap[0])
        {
            heap[0] = nums[i];
            heapify(heap, 0)
        }
    }

    return heap[0]
};

Using max-heap

function kthLargestEl() {
  let nums = [3, 2, 3, 1, 2, 4, 5, 5, 6],
    k = 4;
    
  const heap: number[] = [];

  function heapify(i: number, before?: number) {
    console.log("parent ====  ", i, before);
    // findLargestNumIndex
    const leftIdx = i * 2 + 1;
    const rightIdx = i * 2 + 2;
    let largestIdx = i;

    if (leftIdx < heap.length && heap[leftIdx] > heap[largestIdx]) {
      largestIdx = leftIdx;
    }
    if (rightIdx < heap.length && heap[rightIdx] > heap[largestIdx]) {
      largestIdx = rightIdx;
    }

    // swap
    if (largestIdx !== i) {
      [heap[largestIdx], heap[i]] = [heap[i], heap[largestIdx]];
      heapify(largestIdx, i);
    }
  }

  // buildHeap : O(k) better than O(n) with ...nums entire element.
  heap.push(...nums.slice(0,k)); 

  for (let i = Math.floor(heap.length / 2); i >= 0; i--) {
    heapify(i);
  }

  console.log(heap);
  let result = 0;
  for (let i = 0; i < k; i++) {
    result = heap.pop()!;
  }

  console.log(heap, result);
}

Using Map

function findKthLargest(nums: number[], k: number): number {
  const map = new Map();

  for (const num of nums) {
    map.set(num, (map.get(num) || 0) + 1);
  }

  const minNum = Math.min(...nums);
  const maxNum = Math.max(...nums);

  let count = 0;

  for (let i = maxNum; i >= minNum; i--) {
    if (map.has(i)) {
      count += map.get(i);
    }

    if (count >= k) {
      return i;
    }
  }

  return -1;
}

QuickSelect Algorithm
duplicate values 많은 경우 느림 TLE발생(Time Limit Exceeded)

export function findKthLargest(nums: number[], k: number): number {
  const targetIndex = nums.length - k;

  function partition(left: number, right: number): number {
    const pivot = nums[right];
    let i = left;

    for (let j = left; j < right; j++) {
      if (nums[j] <= pivot) {
        // swap elements
        [nums[i], nums[j]] = [nums[j], nums[i]];
        i++;
      }
    }
    [nums[i], nums[right]] = [nums[right], nums[i]];
    return i;
  }

  function quickSelect(left: number, right: number): number {
    const pivotIndex = partition(left, right);
    if (pivotIndex === targetIndex) {
      return nums[pivotIndex];
    } else if (pivotIndex < targetIndex) {
      return quickSelect(pivotIndex + 1, right);
    } else {
      return quickSelect(left, pivotIndex - 1);
    }
  }

  return quickSelect(0, nums.length - 1);
}

QuickSelect Algorithm

function findKthLargest(nums: number[], k: number): number {
  const targetIndex = nums.length - k;

  function partition(left: number, right: number): [number, number] {
    const randomIndex = left + Math.floor(Math.random() * (right - left + 1));

    [nums[randomIndex], nums[right]] = [nums[right], nums[randomIndex]];

    const pivot = nums[right];
    let i = left,
      j = left,
      n = right;

    while (j <= n) {
      if (nums[j] < pivot) {
        [nums[i], nums[j]] = [nums[j], nums[i]];
        i++;
        j++;
      } else if (nums[j] > pivot) {
        [nums[j], nums[right]] = [nums[right], nums[j]];
        n--;
      } else {
        j++;
      }
    }

    return [i, n];
  }

  function quickSelect(left: number, right: number): number {
    const [low, high] = partition(left, right);
    if (targetIndex >= low && targetIndex <= high) {
      return nums[targetIndex];
    } else if (targetIndex < low) {
      return quickSelect(left, low - 1);
    } else {
      return quickSelect(high + 1, right);
    }
  }

  return quickSelect(0, nums.length - 1);
}

Using MaxHeap Class

function findKthLargest4WithClass(nums: number[], k: number): number {
  let heap = new MaxHeap(nums);
  let result: number = 0;
  for (let i = 0; i < k; i++) {
    result = heap.pop();
  }

  return result;
}

class MaxHeap {
  heap: number[] = [];

  constructor(nums: number[]) {
    this.heap = [];
    this.buildHeap(nums);
  }

  leftChildIndx(parent: number) {
    return parent * 2 + 1;
  }
  rightChildIndex(parent: number) {
    return parent * 2 + 2;
  }

  swap(a: number, b: number) {
    [this.heap[a], this.heap[b]] = [this.heap[b], this.heap[a]];
  }

  findLargestIndex(parent: number) {
    const left = this.leftChildIndx(parent);
    const right = this.rightChildIndex(parent);

    let largest = parent;
    if (left < this.heap.length && this.heap[left] > this.heap[largest]) {
      largest = left;
    }

    if (right < this.heap.length && this.heap[right] > this.heap[largest]) {
      largest = right;
    }

    return largest;
  }

  filterDown() {
    let index = 0;
    while (index < this.heap.length) {
      let largest = this.findLargestIndex(index);
      if (largest !== index) {
        this.swap(index, largest);
        index = largest;
      } else {
        break;
      }
    }
  }

  pop() {
    let result = this.heap[0];
    this.heap[0] = this.heap.pop()!;
    this.filterDown();

    return result;
  }

  buildHeap(arr: number[]) {
    this.heap.push(...arr);

    const n = arr.length;

    const heapify = (index: number) => {
      let largest = this.findLargestIndex(index);

      if (largest !== index) {
        this.swap(largest, index);
        heapify(largest);
      }
    };

    for (let i = Math.floor(n / 2); i >= 0; i--) {
      heapify(i);
    }
  }
}

2. Top K Frequent Elements (LeetCode #347)

Using heap

// heap
export function topKFrequentHeap(nums: number[], k: number): number[] {
  const freqMap = new Map<number, number>();

  for (const num of nums) {
    freqMap.set(num, (freqMap.get(num) || 0) + 1);
  }

  const maxHeap: HeapItem[] = Array.from(freqMap.entries()).map(
    ([num, freqCnt]) => ({ num, freqCnt })
  );

  function findBiggerChildIdx(parentIdx: number) {
    let largest = parentIdx;
    const left = parentIdx * 2 + 1;
    const right = parentIdx * 2 + 2;

    if (
      left < maxHeap.length &&
      maxHeap[left].freqCnt > maxHeap[largest].freqCnt
    ) {
      largest = left;
    }

    if (
      right < maxHeap.length &&
      maxHeap[right].freqCnt > maxHeap[largest].freqCnt
    ) {
      largest = right;
    }

    return largest;
  }

  function heapify(parentIdx: number) {
    const largestChildIdx = findBiggerChildIdx(parentIdx);

    if (largestChildIdx !== parentIdx) {
      [maxHeap[parentIdx], maxHeap[largestChildIdx]] = [
        maxHeap[largestChildIdx],
        maxHeap[parentIdx],
      ];

      heapify(largestChildIdx);
    }
  }

  function pop() {
    const largest = maxHeap[0];

    if (maxHeap.length > 1) {
      maxHeap[0] = maxHeap.pop()!;

      let index = 0;
      while (index < maxHeap.length) {
        const largestChildIdx = findBiggerChildIdx(index);
        if (index !== largestChildIdx) {
          [maxHeap[index], maxHeap[largestChildIdx]] = [
            maxHeap[largestChildIdx],
            maxHeap[index],
          ];

          index = largestChildIdx;
        } else {
          break;
        }
      }
    }

    return largest.num;
  }

  // build heap
  for (let i = Math.floor(maxHeap.length / 2) - 1; i >= 0; i--) {
    heapify(i);
  }

  const result = [];
  for (let i = 0; i < k; i++) {
    result.push(pop());
  }

  return result;
}

Using map and sort

function topKFrequent(nums: number[], k: number): number[] {
  const freq = new Map<number, number>();

  for (const num of nums) {
    freq.set(num, (freq.get(num) || 0) + 1);
  }

  return Array.from(freq)
    .sort((a, b) => b[1] - a[1])
    .slice(0, k)
    .map((val) => Number(val[0]));
}

3. Find K Pairs with Smallest Sums (LeetCode #373)

Using min-heap

// (a,b) => a[0] - b[0]
type CompareFn<T> = (a: T, b: T) => number;

class BinaryMinHeap<T> {
  heap: T[];

  compare: CompareFn<T>;

  constructor(compareFn: CompareFn<T>) {
    this.heap = [];
    this.compare = compareFn;
  }

  pop(): T | undefined {
    if (this.heap.length < 2) {
      return this.heap.pop();
    }

    const samllest = this.heap[0];

    this.heap[0] = this.heap.pop()!;

    this.sinkDown(this.heap, this.compare, 0);

    return samllest;
  }

  push(value: T): number {
    const length = this.heap.push(value);
    this.bubbleUp(this.heap, this.compare, length - 1);
    return length;
  }

  bubbleUp<T>(arr: Array<T>, compareFn: CompareFn<T>, index: number) {
    const value = arr[index];

    while (index > 0) {
      // Math.floor((index - 1) / 2);
      const parentIndex = (index - 1) >> 1;
      if (compareFn(arr[parentIndex], value) <= 0) {
        break;
      }

      arr[index] = arr[parentIndex];
      index = parentIndex;
    }

    arr[index] = value;
  }

  // sinkDown<T>(arr: Array<T>, compareFn: CompareFn<T>, parentIdx: number) {
  //   const N = arr.length;

  //   // Find the indices of the two children (left and right) of the parent
  //   const leftChildIdx = 2 * parentIdx + 1;
  //   const rightChildIdx = 2 * parentIdx + 2;

  //   // Find the index of the smallest (or largest in case of a max-heap) child
  //   let smallestChildIdx = parentIdx;

  //   // Check if the left child exists and is smaller than the current element
  //   if (
  //     leftChildIdx < N &&
  //     compareFn(arr[leftChildIdx], arr[smallestChildIdx]) < 0
  //   ) {
  //     smallestChildIdx = leftChildIdx;
  //   }

  //   // Check if the right child exists and is smaller than the current element
  //   if (
  //     rightChildIdx < N &&
  //     compareFn(arr[rightChildIdx], arr[smallestChildIdx]) < 0
  //   ) {
  //     smallestChildIdx = rightChildIdx;
  //   }

  //   // If the smallest child is different from the parent, swap and recursively heapify
  //   if (smallestChildIdx !== parentIdx) {
  //     [arr[parentIdx], arr[smallestChildIdx]] = [
  //       arr[smallestChildIdx],
  //       arr[parentIdx],
  //     ];

  //     // Recursively heapify the affected subtree
  //     this.sinkDown(arr, compareFn, smallestChildIdx);
  //   }
  // }

  
  sinkDown<T>(arr: Array<T>, compareFn: CompareFn<T>, index: number) {
    const value = arr[index];
    const N = arr.length;
    const mid = Math.floor(arr.length / 2) - 1;
    // const mid = (N - 1) / 2;

    while (index <= mid) {
      let childIndex = (index << 1) + 1;

      // +(true) = 1 , +(false) = 0
      childIndex += +(
        childIndex + 1 < N &&
        compareFn(arr[childIndex + 1], arr[childIndex]) <= 0
      );

      if (compareFn(value, arr[childIndex]) <= 0) {
        break;
      }

      arr[index] = arr[childIndex];
      index = childIndex;
    }
    arr[index] = value;
  }
}

type HeapItem = [sum: number, nums1Value: number, nums2Index: number];
function kSmallestPairs(
  nums1: number[],
  nums2: number[],
  k: number
): number[][] {
  const result: number[][] = [];
  if (nums1.length === 0 || nums2.length === 0 || k === 0) return result;

  const minHeap = new BinaryMinHeap<HeapItem>((a, b) => a[0] - b[0]);

  const N = Math.min(nums1.length, k);
  const M = Math.min(nums2.length, k);

  for (let i = 0; i < N; i++) {
    minHeap.push([nums1[i] + nums2[0], nums1[i], 0]);
  }

  while (k-- > 0 && minHeap.heap.length > 0) {
    const [sum, nums1Value, nums2Index] = minHeap.pop()!;

    result.push([nums1Value, sum - nums1Value]);

    if (nums2Index + 1 < M) {
      minHeap.push([
        nums1Value + nums2[nums2Index + 1],
        nums1Value,
        nums2Index + 1,
      ]);
    }
  }

  return result;
}

Using min-heap2

function kSmallestPairs(
  nums1: number[],
  nums2: number[],
  k: number
): number[][] {
  const result: number[][] = Array.from({ length: k }, () => []);

  const length = result.length;

  const minHeap = new MinHeap();

  for (let i = 0; i < Math.min(nums1.length, k); ++i) {
    minHeap.insert({
      sum: nums1[i] + nums2[0],
      num1: nums1[i],
      num2: nums2[0],
      index2: 0,
    });
  }

  while (k > 0 && !minHeap.isEmpty()) {
    const { num1, num2, index2 } = minHeap.pop();
    result[length - k] = [num1, num2];

    const nextIndex2 = index2 + 1;

    if (nextIndex2 < nums2.length) {
      minHeap.insert({
        sum: num1 + nums2[nextIndex2],
        num1,
        num2: nums2[nextIndex2],
        index2: nextIndex2,
      });
    }

    --k;
  }

  return result;
}


interface INode {
  sum: number;
  num1: number;
  num2: number;
  index2: number;
}

class MinHeap {
  private nodes: INode[] = [];

  constructor() {
    this.nodes = [];
  }

  private swap(a: number, b: number) {
    [this.nodes[a], this.nodes[b]] = [this.nodes[b], this.nodes[a]];
  }

  private shouldSwap(parentIdx: number, childIdx: number) {
    if (parentIdx < 0 || parentIdx >= this.size()) {
      return false;
    }
    if (childIdx < 0 || childIdx >= this.size()) {
      return false;
    }

    return this.nodes[parentIdx].sum > this.nodes[childIdx].sum;
  }

  private heapifyUp(startIdx: number) {
    let childIndex = startIdx;
    let parentIndex = Math.floor((childIndex - 1) / 2);

    while (this.shouldSwap(parentIndex, childIndex)) {
      this.swap(parentIndex, childIndex);
      childIndex = parentIndex;

      parentIndex = Math.floor((childIndex - 1) / 2);
    }
  }

  private heapifyDown(startIdx: number) {
    const length = this.size();
    const leftChildIndex = 2 * startIdx + 1;
    const rightChildIndex = 2 * startIdx + 2;

    let samllest = startIdx;

    if (
      leftChildIndex < length &&
      this.nodes[leftChildIndex].sum < this.nodes[samllest].sum
    ) {
      samllest = leftChildIndex;
    }

    if (
      rightChildIndex < length &&
      this.nodes[rightChildIndex].sum < this.nodes[samllest].sum
    ) {
      samllest = rightChildIndex;
    }

    if (samllest !== startIdx) {
      this.swap(startIdx, samllest);
      this.heapifyDown(samllest);
    }
  }

  size() {
    return this.nodes.length;
  }

  isEmpty() {
    return this.size() === 0;
  }

  insert(value: INode) {
    this.nodes.push(value);
    this.heapifyUp(this.size() - 1);
  }

  pop() {
    if (this.size() === 1) {
      return this.nodes.pop()!;
    }

    const minValue = this.nodes[0];
    this.nodes[0] = this.nodes.pop()!;

    this.heapifyDown(0);

    return minValue;
  }
}