[Algorithm] NSL/NSR - Monotonic stack - leetcode 84

NSL : Nearest Smaller to Left
NSR : Nearest Smaller to Right

순차적 대소 비교
스트림내에서 단일값에 대해 가장 가까운 최소값 / 최대값을 찾을 때
전체 데이터에서 그다음 나오는 가장 가까운 작은값 / 큰값을 찾을 때

NSL : Nearest Smaller to Left

function NSL(nums: number[]) {
    const nearestMinLeft = [];
    const stack = [];

    // index move like left To right but find value on the left side
    for (let i = 0; i < nums.length; i++) {
      while (stack.length && nums[stack[stack.length - 1]] >= nums[i]) {
        stack.pop();
      }
      nearestMinLeft[i] = stack[stack.length - 1] ?? -1;
      stack.push(i);
    }

    return nearestMinLeft;
  }

NSR : Nearest Smaller to Right

function NSR(nums: number[]) {
    const nearestMinRight = [];
    const stack = [];
    // index move like left To right but find value on the right side
    for (let i = nums.length - 1; i >= 0; i--) {
      while (stack.length && nums[stack[stack.length - 1]] >= nums[i]) {
        stack.pop();
      }

      nearestMinRight[i] = stack[stack.length - 1] ?? nums.length;
      stack.push(i);
    }

    return nearestMinRight;
  }

Usage - monotonic stack - leetcode 84

Solution-1

/**
 * Analyzing + NSL/NSR Algorithm : O(n)
 * 전체 배열(히스토그램)의 특정 요소를 기준으로 왼쪽과 오른쪽에 대해서 해당 알고리즘을 바탕으로
 * 가장 가까운 작은 요소의 위치를 찾아 이를 저장한다
 * 그 다음엔 전체 요소에 대해서 다음 식을 반복하는데, 해당 식은
 * (현재 요소의 높이 * (해당 요소의 가장 가까운 오른쪽의 값 - 해당 요소의 가장 가까운 왼쪽의 값 - 1)이다.
 * */

export function largestRectagleAreaWithAnalysis(heights: number[]) {
  let maxArea = 0;
  let nearestMinLeft = [],
    nearestMinRight = [];
  let stack = [];

  function NSL(nums: number[]) {
    const nearestMinLeft = [];
    const stack = [];

    // index move like left To right but find value on the left side
    for (let i = 0; i < nums.length; i++) {
      while (stack.length && nums[stack[stack.length - 1]] >= nums[i]) {
        stack.pop();
      }
      nearestMinLeft[i] = stack[stack.length - 1] ?? -1;
      stack.push(i);
    }

    return nearestMinLeft;
  }

  function NSR(nums: number[]) {
    const nearestMinRight = [];
    const stack = [];
    // index move like left To right but find value on the right side
    for (let i = nums.length - 1; i >= 0; i--) {
      while (stack.length && nums[stack[stack.length - 1]] >= nums[i]) {
        stack.pop();
      }

      nearestMinRight[i] = stack[stack.length - 1] ?? nums.length;
      stack.push(i);
    }

    return nearestMinRight;
  }

  nearestMinLeft = NSL(heights);
  nearestMinRight = NSR(heights);

  /// 자신의 높이 * (오른쪽의 가장 가까운 작은 값 인덱스 - 왼쪽의 가장 가까운 작은 값 인덱스 - 1)
  for (let i = 0; i < heights.length; i++) {
    const h = heights[i];
    const w = nearestMinRight[i] - nearestMinLeft[i] - 1;
    maxArea = Math.max(maxArea, h * w);
  }

  return maxArea;
}

why -1? nearestMinRight[i] - nearestMinLeft[i] - 1;

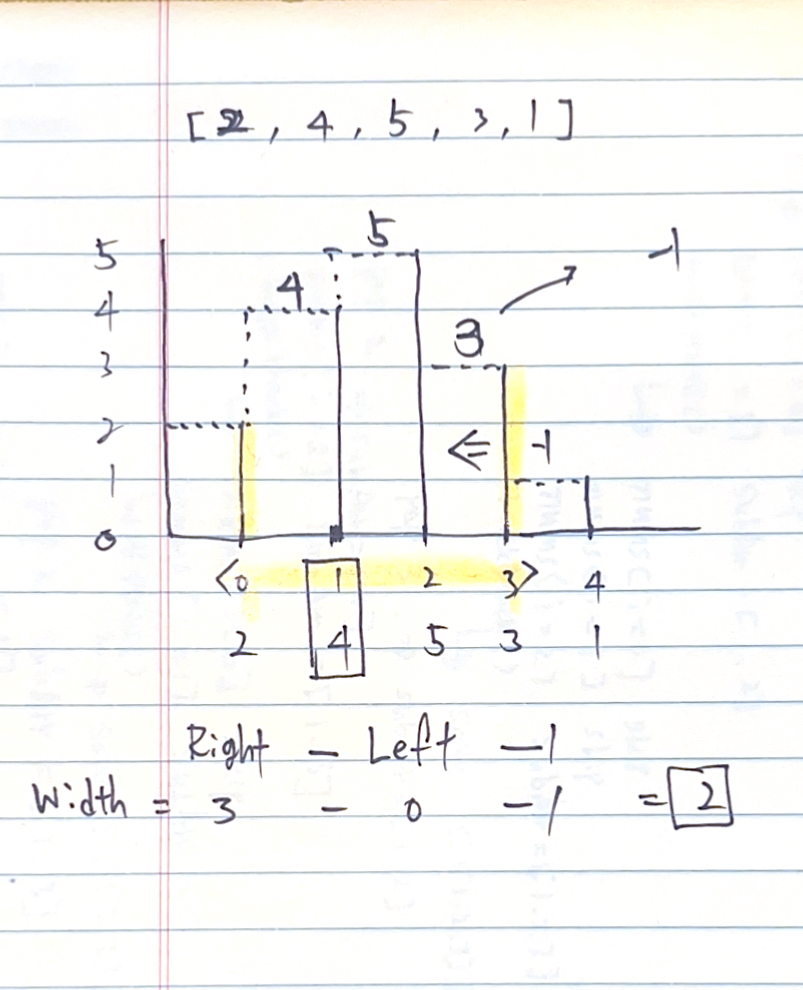
Phase

(Phase 1)
let heights = [ 2, 4, 5, 3, 1 ] 
let index = 0 ; 
let nearestMinLeft = [ -1, 0, 1, 0, -1 ]
let nearestMinRight =[ 4, 3, 3, 4, 5 ];
let h = heights[index];
let left = nearestMinLeft[index]
let right = nearestMinRight[index];
`${right} -(${left}) -1 : ${right - left - 1}`
width: '4 -(-1) -1 : 4'

(Phase 2)
let heights = [ 2, 4, 5, 3, 1 ] 
let index = 1 ; 
let nearestMinLeft = [ -1, 0, 1, 0, -1 ]
let nearestMinRight =[ 4, 3, 3, 4, 5 ];
let h = heights[index];
let left = nearestMinLeft[index]
let right = nearestMinRight[index];
`${right} -(${left}) -1 : ${right - left - 1}`
width: '3 -(0) -1 : 2'

(Phase 3)
let heights = [ 2, 4, 5, 3, 1 ] 
let index = 2; 
let nearestMinLeft = [ -1, 0, 1, 0, -1 ]
let nearestMinRight =[ 4, 3, 3, 4, 5 ];
let h = heights[index];
let left = nearestMinLeft[index]
let right = nearestMinRight[index];
`${right} -(${left}) -1 : ${right - left - 1}`
width: '3 -(1) -1 : 1'

(Phase 4)
let heights = [ 2, 4, 5, 3, 1 ] 
let index = 3; 
let nearestMinLeft = [ -1, 0, 1, 0, -1 ]
let nearestMinRight =[ 4, 3, 3, 4, 5 ];
let h = heights[index];
let left = nearestMinLeft[index]
let right = nearestMinRight[index];
`${right} -(${left}) -1 : ${right - left - 1}`
width: '4 -(0) -1 : 3'

(Phase 5)
let heights = [ 2, 4, 5, 3, 1 ] 
let index = 4; 
let nearestMinLeft = [ -1, 0, 1, 0, -1 ]
let nearestMinRight =[ 4, 3, 3, 4, 5 ];
let h = heights[index];
let left = nearestMinLeft[index]
let right = nearestMinRight[index];
`${right} -(${left}) -1 : ${right - left - 1}`
width: '5 -(-1) -1 : 5'

Solution-2

// this one is east to understand and explain
export function largestRectangleAreaPassed(heights: number[]): number {
  const stack: [number, number][] = [];
  let maxArea = 0;

  for (let i = 0; i < heights.length; i++) {
    let start = i;

    const currH = heights[i];
    while (stack.length > 0 && stack[stack.length - 1][1] > currH) {
      const [index, height] = stack.pop()!;
      maxArea = Math.max(maxArea, height * (i - index));
      start = index;
    }

    stack.push([start, currH]);
  }

  for (const [index, height] of stack) {
    maxArea = Math.max(maxArea, height * (heights.length - index));
  }

  return maxArea;
}