[Big 0] Algorithm - Complexity

Darcy Daeseok YU ·2025년 1월 18일

Complexity

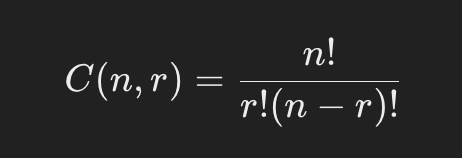
O(n)

참고사이트

알고리즘이란

어떤 목적을 달성하거나 결과물을 만들어내기 위해 거쳐야 하는 일련의 과정들을 의미한다.

과정의 루트는 다양하며, 여러가지 상황에 따른 알고리즘은 모두 다르다. 따라서 시간복잡도가 가장 낮은 알고리즘을 선택해야 한다.

알고리즘 실행시간 = 알고리즘 코드를 실행하는 속도 = 컴퓨터의 처리속도/사용된 언어종류/컴파일러 속도

알고리즘 실행시간(속도) 검증

입력값의 크기에 따라 검증할 수 있고, 입력값의 크기에 따른 함수의 증가량을 성장률이라 부른다. 이때 중요하지 않은 상수와 계수들을 제거하면 알고리즘의 실행시간에서 중요한 성장률에 집중할 수 있는데 이것을 점금적 표기법이라 부른다. (점근적 표기 : 가장 큰 영향을 주는 항만 계산한다는 의미)

점근적 표기법 (시간복잡도 나타냄)

최상의 경우(BEST CASE) : 오메가 표기법
평균의 경우 : 세타 표기법
최악의 경우(Worst CASE) : 빅오 표기법

평균인 세타 표기법이 좋으나, 평가하기가 까다롭다.

중요하지 않은 상수 / 계수 제거

an^3 + 100 + an^4 + 10 + an^2

a 계수
^2 차수
100 상수
^4 최고차항
O(n^4) :: n이 무한대로 가면 n^4보다 작은 값은 영향력이 미미함.

Time Complexity 예제

Iterations=(End − Start) + 1 -> n번 실행

// 1) for i <- 0 to n 

for(i = 0 ; i <= n; i++) //O(n) :: (n - 0 + 1) => n 

// 2) for i <- 1 to n 

for(i = 1; i <= n; i++) //O(n) :: (n - 1 + 1) => n 

// 3) for i <- 1 to n - 1

for(i = 3; i <= n - 1; i++) //O(n) :: ((n - 1) - 3 + 1) => n - 3

MenOfPassion(A[], n) {
    sum <- 0; // O(1) 
    for i <- 1 to n - 1 // O(n) 
        for j <- i + 1 to n // O(n) :: (n - 1 + 1)
            sum <- sum + A[i] × A[j]; # 코드1
    return sum; O(1)
}

다항식
1 + (n - 1 - 1) * (n - 1 + 1) + 1

결과 :: O(n^2)

백준 24267

MenOfPassion(A[], n) {
    sum <- 0;
    for i <- 1 to n - 2
        for j <- i + 1 to n - 1
            for k <- j + 1 to n
                sum <- sum + A[i] × A[j] × A[k]; # 코드1
    return sum;
}