[백준 2618번] 경찰차

mokomoko·2022년 1월 30일

1. 문제

어떤 도시의 중심가는 N개의 동서방향 도로와 N개의 남북방향 도로로 구성되어 있다.

모든 도로에는 도로 번호가 있으며 남북방향 도로는 왼쪽부터 1에서 시작하여 N까지 번호가 할당되어 있고 동서방향 도로는 위부터 1에서 시작하여 N까지 번호가 할당되어 있다. 또한 동서방향 도로 사이의 거리와 남 북방향 도로 사이의 거리는 모두 1이다. 동서방향 도로와 남북방향 도로가 교차하는 교차로의 위치는 두 도로의 번호의 쌍인 (동서방향 도로 번호, 남북방향 도로 번호)로 나타낸다. N이 6인 경우의 예를 들면 다음과 같다.

이 도시에는 두 대의 경찰차가 있으며 두 차를 경찰차1과 경찰차2로 부른다. 처음에는 항상 경찰차1은 (1, 1)의 위치에 있고 경찰차2는 (N, N)의 위치에 있다. 경찰 본부에서는 처리할 사건이 있으면 그 사건이 발생된 위치를 두 대의 경찰차 중 하나에 알려 주고, 연락 받은 경찰차는 그 위치로 가장 빠른 길을 통해 이동하여 사건을 처리한다. (하나의 사건은 한 대의 경찰차가 처리한다.) 그리고 사건을 처리 한 경찰차는 경찰 본부로부터 다음 연락이 올 때까지 처리한 사건이 발생한 위치에서 기다린다. 경찰 본부에서는 사건이 발생한 순서대로 두 대의 경찰차에 맡기려고 한다. 처리해야 될 사건들은 항상 교차로에서 발생하며 경찰 본부에서는 이러한 사건들을 나누어 두 대의 경찰차에 맡기되, 두 대의 경찰차들이 이동하는 거리의 합을 최소화 하도록 사건을 맡기려고 한다.

예를 들어 앞의 그림처럼 N=6인 경우, 처리해야 하는 사건들이 3개 있고 그 사건들이 발생된 위치 를 순서대로 (3, 5), (5, 5), (2, 3)이라고 하자. (3, 5)의 사건을 경찰차2에 맡기고 (5, 5)의 사건도 경찰차2에 맡기며, (2, 3)의 사건을 경찰차1에 맡기면 두 차가 이동한 거리의 합은 4 + 2 + 3 = 9가 되 고, 더 이상 줄일 수는 없다.

처리해야 할 사건들이 순서대로 주어질 때, 두 대의 경찰차가 이동하는 거리의 합을 최소화 하도록 사건들을 맡기는 프로그램을 작성하시오.

제한 사항

시간 : 1 초
메모리 : 128 MB

입력

첫째 줄에는 동서방향 도로의 개수를 나타내는 정수 N(5 ≤ N ≤ 1,000)이 주어진다. 둘째 줄에는 처리해야 하는 사건의 개수를 나타내는 정수 W(1 ≤ W ≤ 1,000)가 주어진다. 셋째 줄부터 (W+2)번째 줄까지 사건이 발생된 위치가 한 줄에 하나씩 주어진다. 경찰차들은 이 사건들을 주어진 순서대로 처리해야 한다. 각 위치는 동서방향 도로 번호를 나타내는 정수와 남북방향 도로 번호를 나타내는 정수로 주어지며 두 정수 사이에는 빈칸이 하나 있다. 두 사건이 발생한 위치가 같을 수 있다.

출력

첫째 줄에 두 경찰차가 이동한 총 거리를 출력한다. 둘째 줄부터 시작하여 (i+1)번째 줄에 i(1 ≤ i ≤ W)번째 사건이 맡겨진 경찰차 번호 1 또는 2를 출력한다.

- 키워드

조금 복잡한 DP와 백트래킹을 사용하자.

절대로 PyPy3 로 제출하지 마라!

2. 풀이

DP에 대해 부족한 것은 알고 있었지만, 이 문제는 많이 골치아팠던 거 같았다.

문제를 이해하고 푸는 데 하루를 다 썼고, 무엇보다 같이 해야했던 편집작업도 있어서

작성하는 데 시간이 걸렸던 거 같았다. ~~사실 그것보다 PyPy3때문에 샷건 몇 번 쳤었다...~~

해당 문제의 DP 구조는 다음과 같다.

주어진 N * N 사이즈의 공간에서 특정 지점의 사건을 해결하는 데

경찰차는 단 2대~~단두대~~[(0,0),(N,N)]뿐이다.

단순히 무작정 가깝다고 이동시키면 안된다.

이런 테스트케이스의 경우 (N,N)이 전부 움직일 것이고,

잘못된 답을 도출할 수도 있다.

그렇다면 어떻게 DP를 구현해야할까?

머리를 계속 굴려봤지만, 틀조차 잡히지 않아서 구글 검색을 통해서 여러 방법을 찾아봤다.

일단 공통적으로 다들 풀었던 방식은 다음과 같았다.

DP 그래프를 W+2 사이즈 만큼 만든다.

경찰차 2대를 i , j로 표현한다.

DP[i][j]는 한 대는 i번째, 한 대는 j번째까지 해결한 상태를 저장한다.

탐색할 때는 max(i,j) + 1 을 구하고 search(max(i,j)+1, j), search(i, max(i,j)+1)를 수행한다.

이 문제를 푸는데 dp값 구하기와 역추적이므로 2가지 과정을 설명하려고 한다.

1. DP (최소거리 구하기)

다음 테스트케이스를 살펴보자.

7
5
7 2
5 4
3 6
2 4
2 2

dp를 보드기준이 아닌 W의 값 그리고 position을 기준으로 한다.

dp 그래프의 크기는 W+2로 잡는다. 이유는 경찰차의 초반 position은 (0,0),(N,N)이므로,

W+2 사이즈가 된다.

해당 케이스에서는 [(0,0),(7,7),(7,2),(5,4),(3,6),(2,4),(2,2)]

해당 로직을 search(max(i,j)+1,j)를 제일 먼저하기 때문에,

(0,0)에 있는 경찰차가 모든 일을 다 했을 때이다.

그래프에는 dp[5][1] 값이 가장 먼저 저장 된다. 여기에 저장되는 값은

4번째 사건과 5번째 사건의 거리다.

그 이후로는 사건이 끝났기 때문에 (max(i,j) + 1이 W보다 크므로) 종료시킨다.

그 다음에 4번째 사건으로 돌아가서 dp 그래프에 값이 저장되는데 2개가 저장된다.

방금 전 저장되었던 값 2와 3번째 4번째 사건 거리의 값을 저장한다.

그리고, j가 5번째 사건을 맡을 경우에도 최솟값을 같이 저장한다.

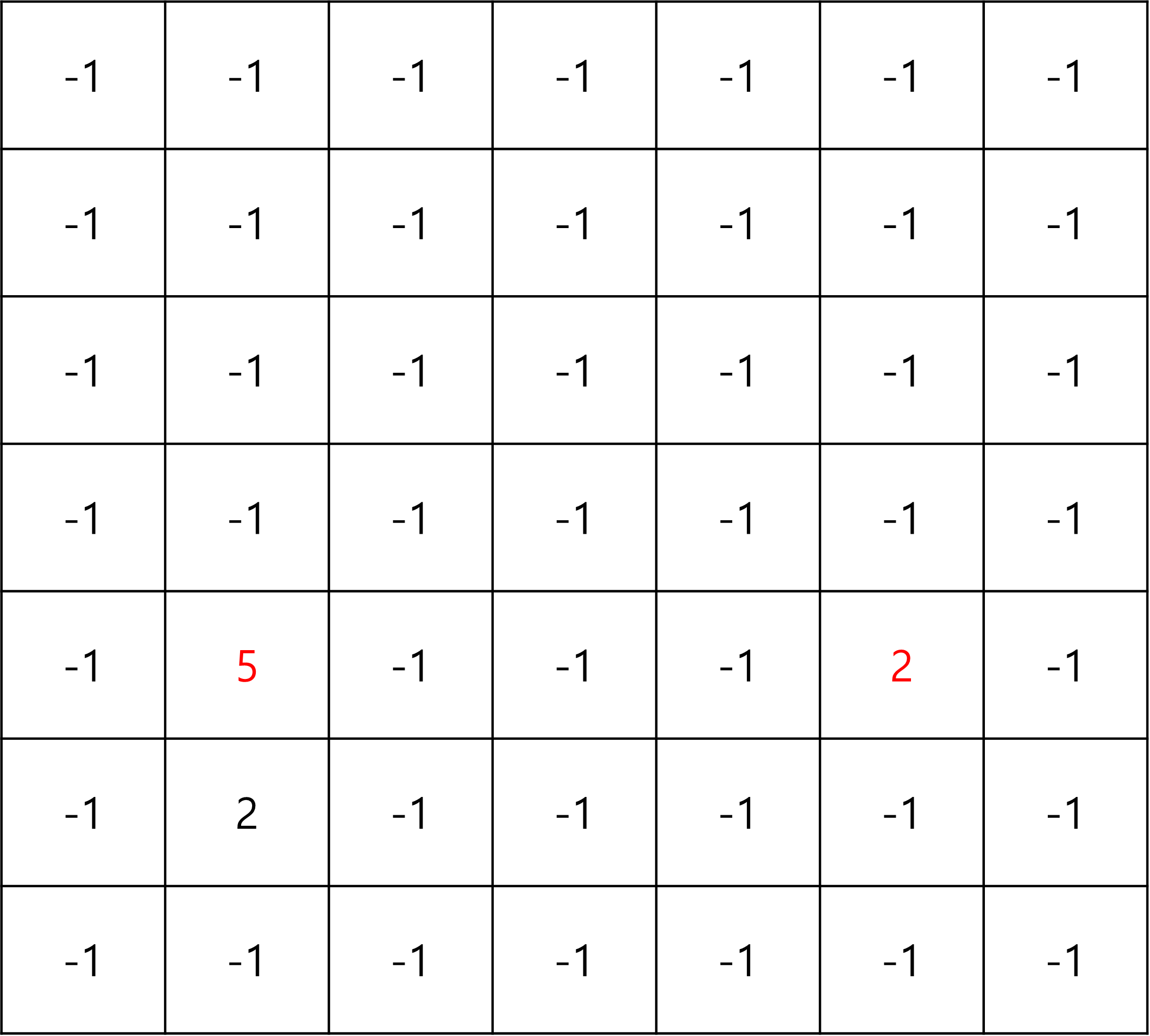
양방향으로 값이 저장이되기 때문에

해당 과정을 비슷하게 적용된다.

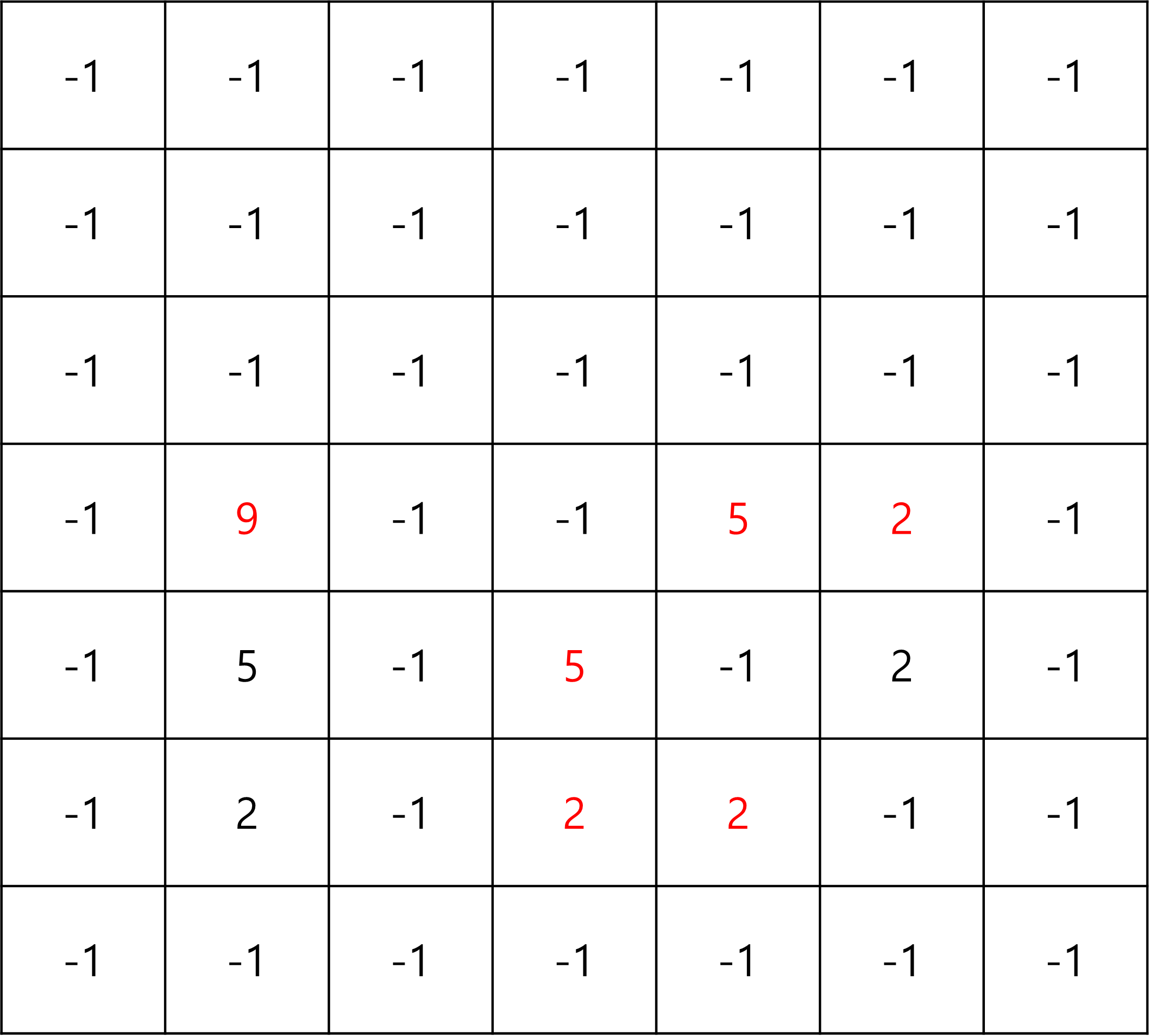
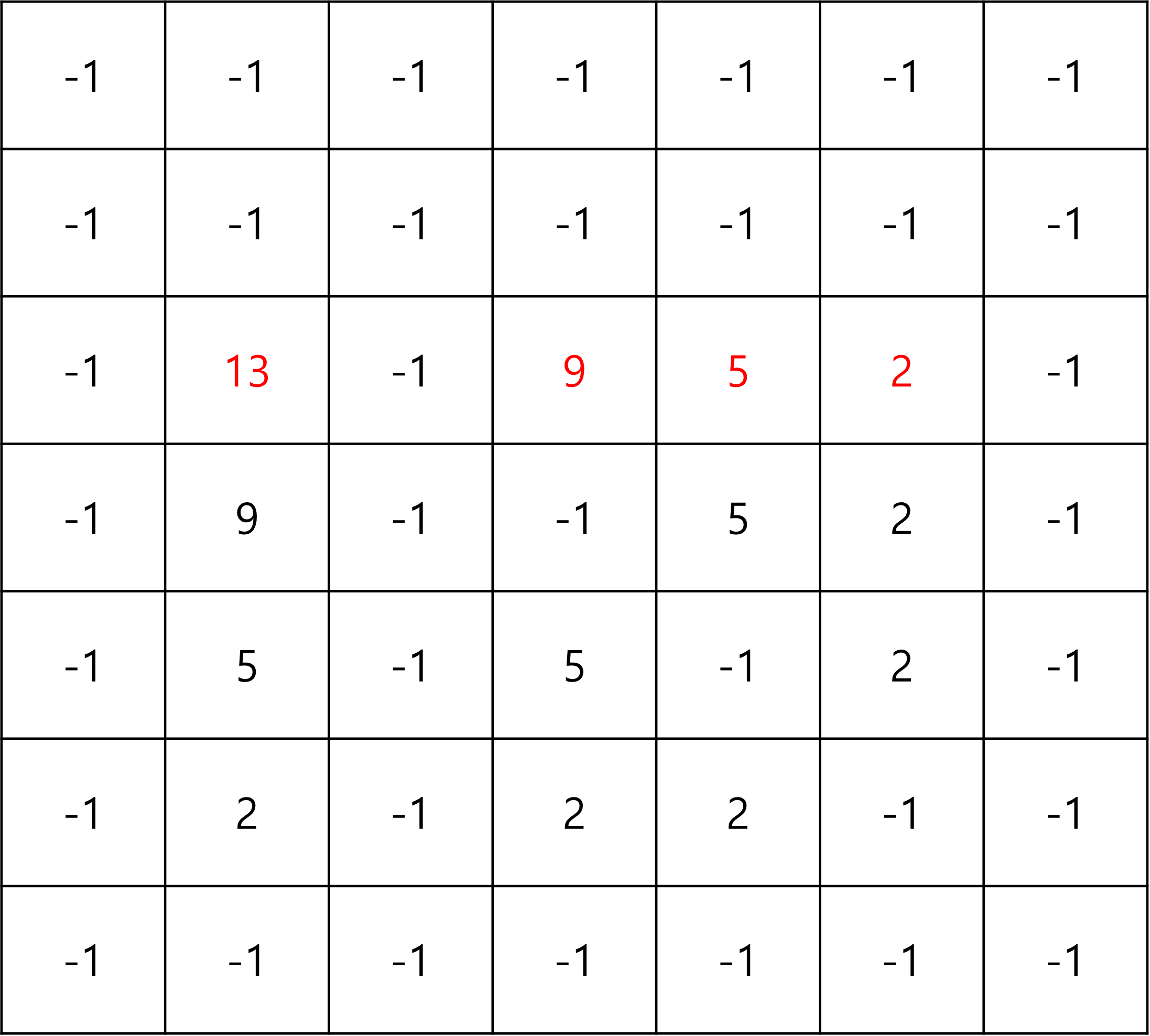
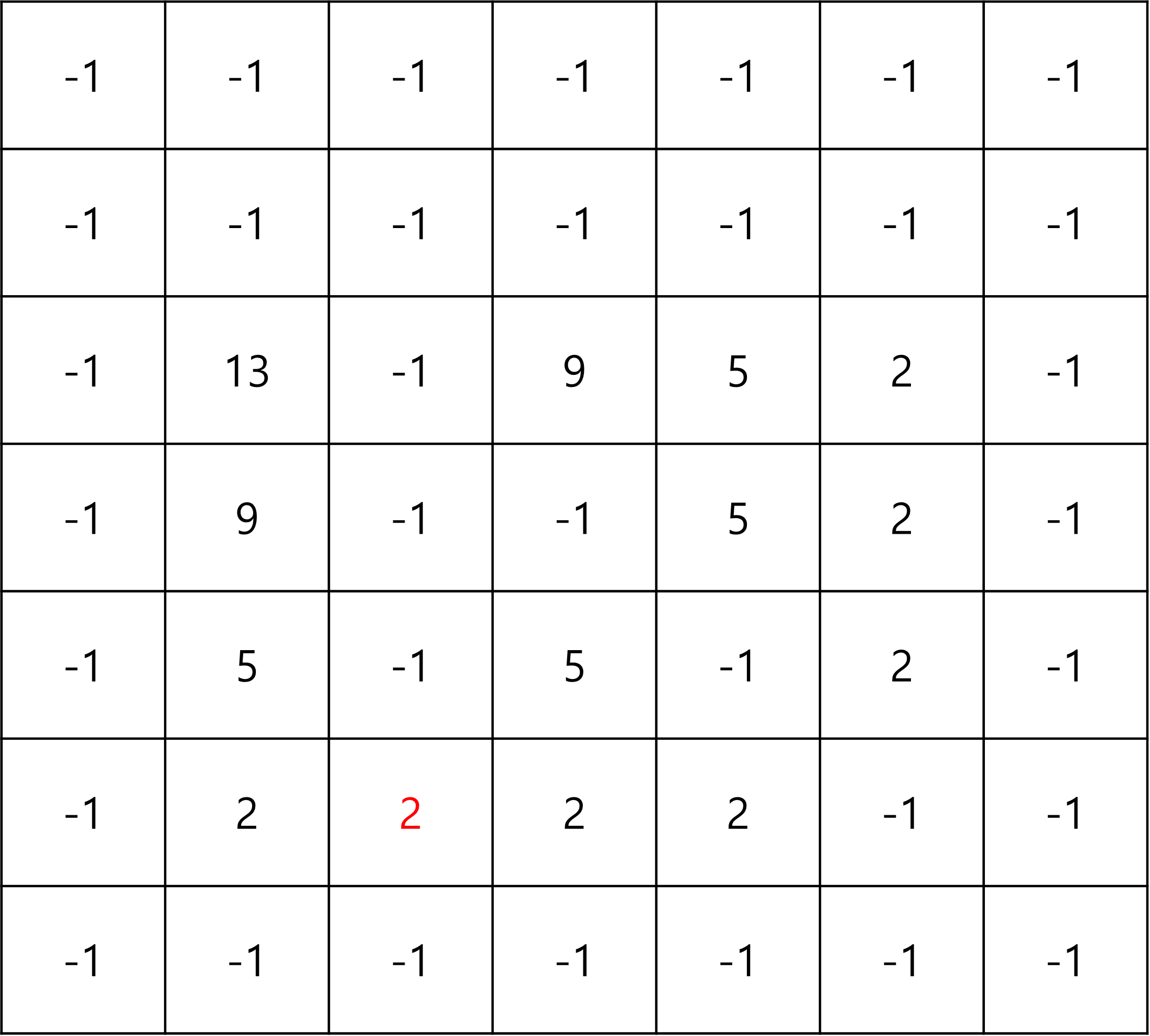
여기까지가 (0,0) 경찰차가 처음부터 진행했을 때이고,

이 이후로는 (N,N) 경찰차가 처음부터 진행했을 때이다.

지금 대다수 dp구간이 저장되어 있고, 최솟값이므로,
-> 각 사건-사건이 최소거리이므로, 각 사건의 거리가 저장되었다.

(N,N) 경찰차가 혼자 일했을 때 값만 저장된다.

모든 경우의 수를 탐색하고 이제 dp[0][1] 에 최소거리가 저장된다.

1번째 사건부터 5번째 사건의 거리의 최소는 13이고,

남은 것은 (0,0)과 (N,N) 중 1번째 사건이 가까운 곳이 저장된다.

1번째 사건은 (N,N) 경찰차와 더 가까우므로

dp[0][1] 에 저장되는 값은 18이다.

최소 거리는 구했지만, 우리는 여기서 끝나서는 안된다.

우리가 왔던 길을 알아야 하므로 역추적을 해야한다.

2. 역추적

이것도 dp와 같이 0,1로 시작한다.

각 경찰차의 위치 - 1번째 사건의 거리와 다음 사건의 거리와의 값을 이용해 추적한다.

dp값을 확인해보자.

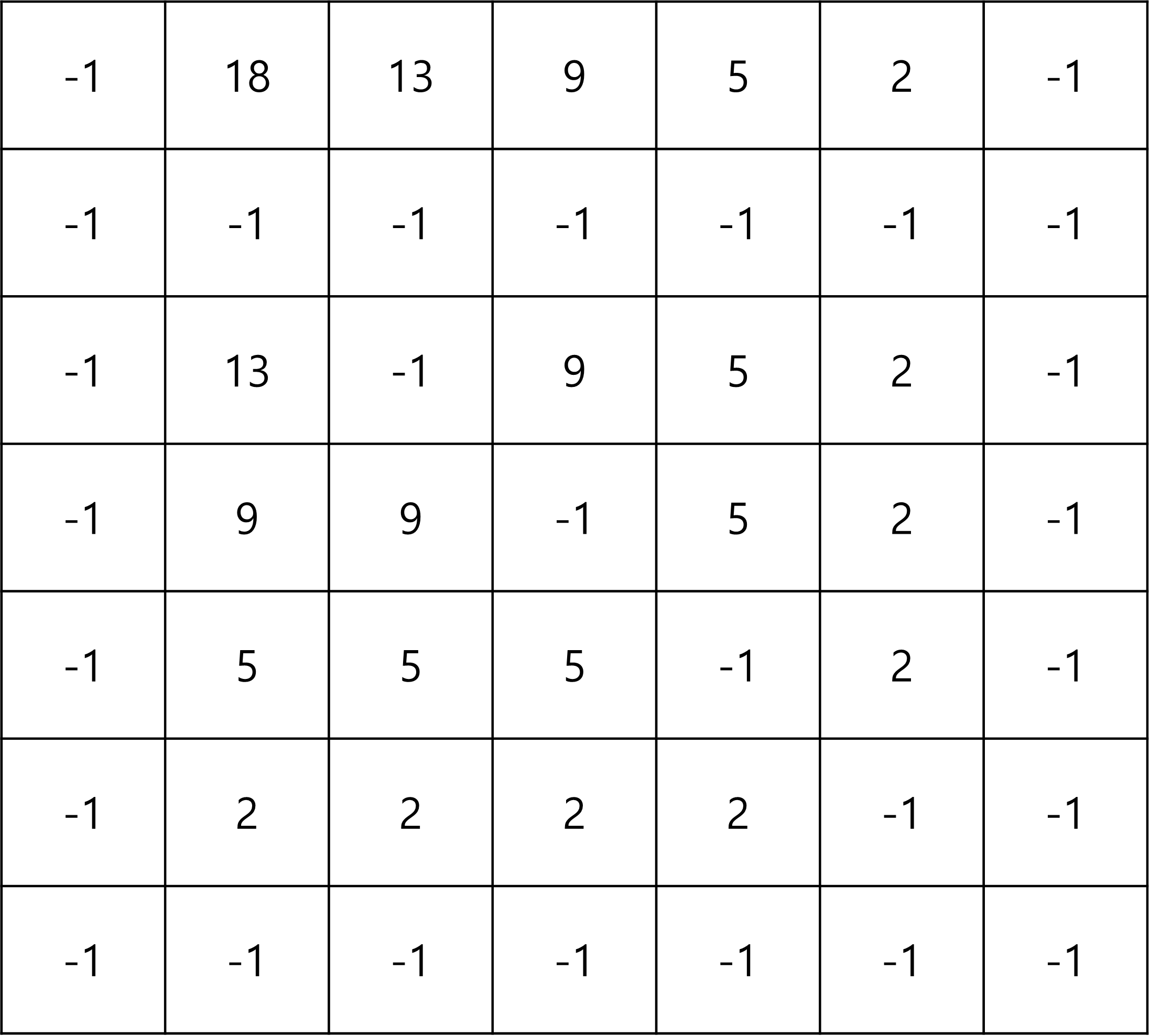
다음 사건의 거리 값은 dp[2][1],dp[0][2] 에 저장되어있다.

둘 다 13이고, 각 경찰차의 위치 - 1번째 사건의 거리는 7,5이다.

그러므로 (N,N) 경찰차이므로 2를 출력한다.

다음은 (0,2) 에서 추적한다.

dp[0][3]과 dp[3][2]에 저장된 값 그리고 각자의 위치 - 2번째 사건 거리를 구한다.

dp[0][3], dp[3][2]에 저장된 값은 9이고,

(0,0)과 (7,2)에서 (5,4) 의 거리는 각각 9,4이므로 2를 출력한다.

다음은 (0,3) 에서 추적을 실행하고 계속 같은 방법으로 추적을 진행한다.

결과값은

18
2
2
2
2
2

이다.

3. 소스코드

import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**6)

N = int(input())
W = int(input())
pos = [(1,1),(N,N)]
dp = [[-1] * (W+2) for _ in range(W+2)]
def search(row,col):
	print(row,col)
	for i in dp:
		print(i)
	print()
	if row > W or col > W:
		return 0
	if dp[row][col] != -1:
		return dp[row][col]
	next_pos = max(row,col) + 1
	nr = search(next_pos,col) + abs(pos[next_pos][0] - pos[row][0]) + abs(pos[next_pos][1] - pos[row][1])
	nc = search(row,next_pos) + abs(pos[next_pos][0] - pos[col][0]) + abs(pos[next_pos][1] - pos[col][1])
	dp[row][col] = min(nr,nc)
	return dp[row][col]

def route(row,col):
	if row > W or col > W:
		return
	next_pos = max(row,col)+1
	nr = abs(pos[next_pos][0]-pos[row][0]) + abs(pos[next_pos][1] - pos[row][1])
	nc = abs(pos[next_pos][0]-pos[col][0]) + abs(pos[next_pos][1] - pos[col][1])

	if dp[next_pos][col]+nr < dp[row][next_pos]+nc:
		print(1)
		route(next_pos,col)
	else:
		print(2)
		route(row,next_pos)
	return

def solution(N,W):
	print(search(0,1))
	for i in dp:
		print(i)
	print()
	route(0,1)

if __name__ == "__main__":
	for _ in range(W):
		pos.append(tuple(map(int,input().split())))
	solution(N,W)