Linear Regression의 Hypothesis와 cost

training data로 regression모델 만듦.
x값에 대한 y값이 주어진 데이터들.
그러한 데이터들로 가설을 세울 수 있음
Linear한 모델을 만들면... Linear Hypotheisis.(선형)

우린 데이터가 주어져 있으면 일차방정식을 예측해서 세울 수 있다.
그런데 어떤 선이 가장 나을지? 어떤 가설이 더 나은 가설일지?

우리는 직선을 그었을 때 실제 데이터 점과 가설로 만든 직선의 차이를 통해서 어떤 게 더 정확한지 판단할 수 있다. 저 데이터 값과 직선의 y값의 거리가 가까울 수록 좋음.

우리는 그 (오차의) 거리를 측정하는 것을 Cost function이라 부른다.
이는 가설의 값에서 실제 데이터 값을 뺀 값과 같다. 하지만 이러한 모델은 좋지 않음!
-> 그럼 그 값을 제곱해서 사용하면 된다. 제곱을 하면 차이 값을 모두 양수로 표현할 수 있으면서도, 거리가 먼 경우 더 패널티를 줄 수 있기 때문이다.

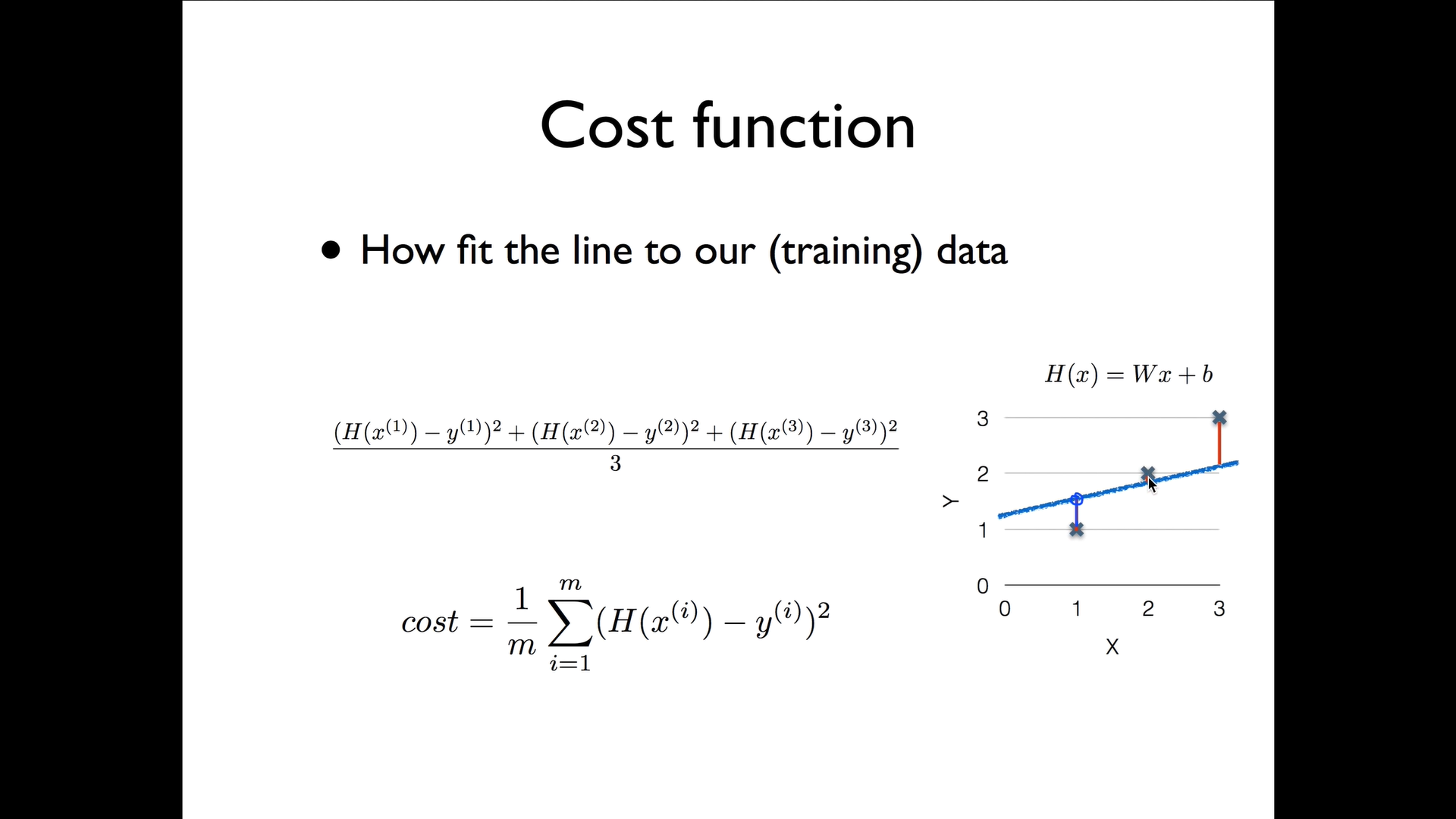
더 정리하자면, 가설 값에서 실제 데이터 값을 뺀 것을 제곱한 값들을 다 더해주고, 데이터의 개수만큼 나눠주면 된다.
우리는 이것을 통계에서 배웠다!! 뭐냐면 바로 분산! 편차의 제곱의 평균을 우리는 분산이라고 배웠다.

참고: https://inf.run/Ndkd

이걸 배우면서 느낀 건 선형대수에서 배운 최소제곱법이 떠올랐다. 새로 배우는 것과 아는 것들을 머리에서 조합하면서 배우는 것의 즐거움을 깨닫게 되는 것 같다.