SWEA 1208. Flatten python(파이썬)

문제 간략 설명

가장 높은 곳의 상자를 하나 빼서 가장 낮은 곳을 채워 올리자.

문제 포인트

count sort의 개념을 얼마나 잘 쓸 수 있는가

알아갈 개념 요약

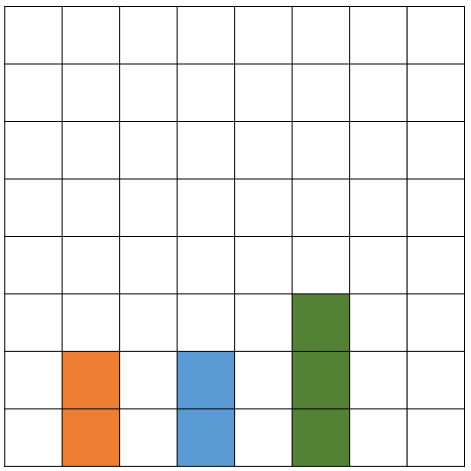
행위의 본질을 이해할 필요가 있다.

• 이 문제의 본질은 이전 층의 값을 계속 가져가는 누적 쌓기.
• 100층이 MAX이므로 1층~100층짜리 건물이 각각 몇개 있는지 리스트로 뽑아낸다!
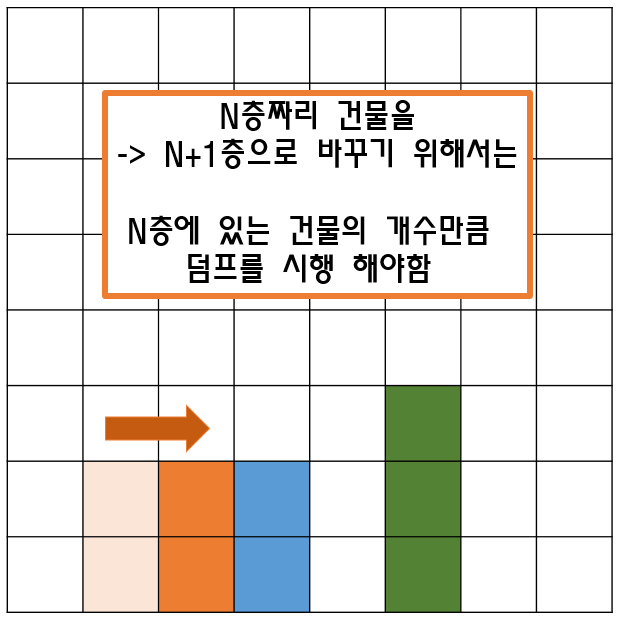
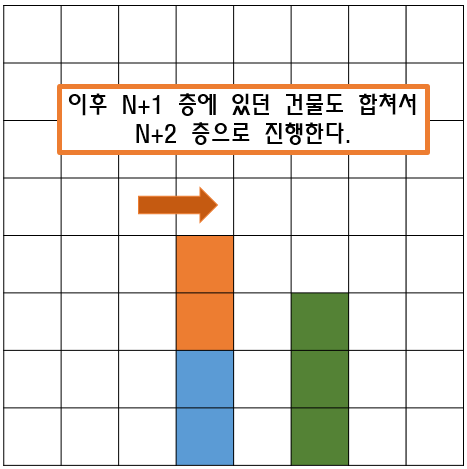
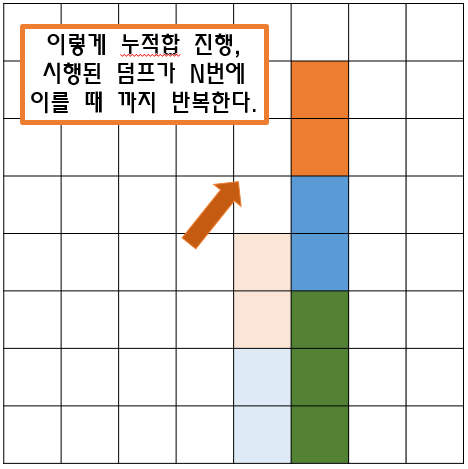
• 이렇게 뽑아낸 리스트의 양 극단에서 덤프를 시행하면 아래와 같은 연산이 가능해진다!
• 덤프의 시행 횟수를 N회라고 했을때,
  • 해당 덤프로 끼워줄 수 있는 상자의 개수가 N개, 뺄 수 있는 상자의 개수가 N개.>

풀이

ㄴN층 짜리 모든 건물에 1층씩 추가하여 N+1층으로

• 풀이

# 1208.Flatten
# 이건 누적합 문제
# 카운팅 리스트 작성하고 앞에서 뒤로 가면서 누적합을 채워주면 된다.
# 반대도 동시에 진행하면 좋겠지만, 따로 진행.

T = 10
for case_num in range(1, T+1):
    N = int(input())
    box_list = list(map(int, input().split()))
    dump_up_list = [0] * 101
    dump_down_list = [0] * 101
    for box in box_list:
        dump_up_list[box] += 1
        dump_down_list[box] += 1
    # 생각해야할 부분은 3개.
    # 1. 밑에서 위로 가는 dump
    # 2. 위에서 아래로 내려오는 dump
    # 3. 그 두 dump가 만나는가의 여부

    dump_up = 0                                             
  # dump_up -> 아래층 부터 누적합을 쌓아가는 덤프 시행횟수
    up_count = 0                                            
  # UP_count -> 몇번 밟았나 = 현재 공사 진행중인 층 수
    
    while dump_up < N and up_count != 101:                  
    # <반복> 아래층부터 한층씩 누적합을 쌓아가며 올라가기
  
        dump_up += dump_up_list[up_count]                   
        # 해당 층의 모든 박스 개수 만큼 덤프 횟수에 추가하고
        
        dump_up_list[up_count + 1] += dump_up_list[up_count]
        # 다음 층에 그 박스 개수만큼 더해줌
        up_count += 1                                       
        # 한 층 올라감
  
    low_box = up_count-1                                    
    # dump_up이 N을 넘어갈 경우 멈추기 때문에,
    # -> 실제로 공사중인 층은 현재 층보다 한칸 아래임.
  
    dump_down = 0
    down_count = 100
    while dump_down < N and down_count != 0:                
      # dump_down -> 최상층 부터 누적합을 쌓아가는 덤프 시행횟수
  
        dump_down += dump_down_list[down_count]             
      # down_count -> 몇번 밟았나 = 현재 공사 진행중인 층 수
  
        dump_down_list[down_count - 1] += dump_down_list[down_count]
        down_count -= 1                                     
        # 한 층 내려감
  
    high_box = down_count+1                                 
    # dump_down이 N을 넘어갈 경우 멈추기 때문에,
    # -> 실제로 공사중인 층은 현재 층보다 한칸 위임.
    if low_box >= high_box:                                 
    # 덤프를 너무 많이 해서 서로 중간에 지나쳐가게 되면, 
        ans = 1                                             
    # 최하층이 최상층보다 같거나 높게 나오므로 1을 반환
    else:
        ans = high_box - low_box
    print(f'#{case_num} {ans}')