[논문리뷰] FKP(Flow-based Kernel Prior with Application to Blind Super-Resolution)

Abstract
커널 추정은 일반적으로 Blind 이미지 Super-resolution의 주요 문제 중 하나입니다. 최근 DoubleDIP는 네트워크 아키텍처를 통해 커널을 모델링 할 것을 제안하는 반면, KernalGAN은 커널 공간을 제한하기 위해 심층 선형 네트워크와 몇가지 정규화 loss를 채택합니다.
그러나 이미지 SR은 anistropic 가우시안 커널이 충분하다는 일반적인 SR 커널의 가정을 충분히 활용하지 못합니다. 이 문제를 해결하기 위해, 본 논문에서는 커널 모델링을 위한 flow-based 커널 prior 표준화(FKP)를 제안합니다.
비등방성 가우스 커널 분포와 다루기 쉬운 잠재 분포 사이의 역함수를 학습함으로써 FKP를 Double DIP 및 Kernal GAN의 커널 모델링 모듈을 쉽게 대체할 수 있습니다. 구체적으로 FKP는 네트워크 매개 변수 공간이 아닌 잠재 공간에서의 커널을 최적화하여 합리적인 커널 초기화를 생성하고 학습된 커널 매니폴드를 통과하며 최적화 안정성을 향상시킬 수 있습니다. 합성 및 실제 이미지에 대한 광범위한 실험은 논문에서 제안된 FKP가 더 적은 매개변수와 Runtime, 메모리 사용으로 커널 추정의 정확도를 크게 향상시켜, 최첨단 blind SR 결과로 이어질 수 있음을 보여줍니다.
모델분석
Flow-based Kernel Prior
- 보통 일반적으로 SR에서의 학습을 위한 degradation LR 이미지를 만들때, blurring과 downsampling을 HR이미지 x에서 수행합니다. 수학적으로는 아래와 같이 수행됩니다.
- 특히 Blind SR은 HR 이미지와 블러 커널을 동시에 예측하는 것을 목표로 합니다. Maximum A Posteriori (MAP)에 따르면 다음과 같이 해결 될 수 있습니다.
-
는 데이터의 충실도 입니다.
-
는 이미지의 Prior를 의미합니다.
-
는 커널의 prior를 의미합니다.
-
와 는 trade-off 파라미터입니다.
-
커널을 잘못 추정하면 HR 이미지 추정 성능이 심각하게 저하될 수 있다는 것은 잘 알려진 사실입니다.
-
하지만 자연 이미지 통계량을 잘 설명하기 위해 다양한 이미지 Prior가 제안되었지만, 커널 Prior 설계에는 거의 주의를 기울이지 않았습니다.
-
이러한 관점에서 논문에서는 kernal prior 기반 학습을 목표로 했습니다.
-
는 커널의 매개변수를 의미한다.
-
는 대응하는 잠재 변수를 의미합니다.
-
와 는 확률분포 와 를 따릅니다.
-
논문에서는 파라미터 와 함께 반론 을 정의합니다.
-
커널 는 잠재 공간의 잠재 변수 에 의해 인코딩 될 수 있습니다.
-
가역적으로 는 역방향 매핑을 통해 정확하게 재구성 될 수 있습니다. 이런식으로요
-
변수 공식의 변화에 따라, 의 확률은 다음과 같이 계산됩니다.
-
는 에 있는 의 야코비안 행렬식입니다.
-
일반적으로 는 다변량 가우스 분포와 같이 단순하고 다루기 쉬운 분포입니다.
-
는 종종 일연의 가역 및 다루기 쉬운 변환으로 구성됩니다.
-
와 저자들은 의 를 가지고있다
-
입력과 출력 의 과 는 각각 와 이다.
-
최대우도 추정에서 음수 로그우도(NLL) 손실을 최소화하여 를 최적화할 수 있습니다.
-
보다 구체적으로, 우리는 가역 유동층을 쌓아서 FKP를 구축합니다.
-
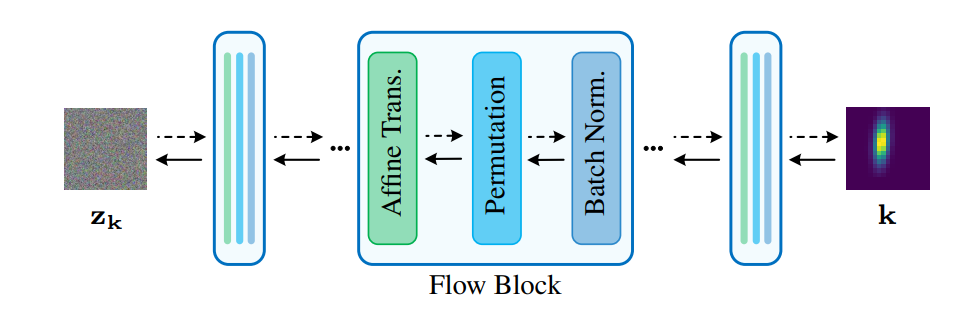
그림 1과 같이, 이 계층은 여러 개의 흐름 블록으로 구성되며, 각 블록에는 배치 정규화 계층, permutation 계층 및 아핀 변환 계층의 3개 연속 계층이 포함됩니다.
-
아핀 변환 계층의 경우 확장 및 전환에 FCN(Small Full-Connected Neural Network)을 사용합니다. 각 FCN은 Fully-connected-layer와 하이퍼볼릭 탄젠트 활성화 계층을 번갈아 쌓습니다.
-
FKP는 학습용 커널 샘플이 주어진 NLL loss에 의해 학습됩니다.

-
그림 2와 같이 임의의 커널에 해당하는 잠복 변수 를 커널로 기존 커널 추정 모델에 연결할 때 먼저 무작위로 샘플링 합니다.
-
그런 다음, 모델 매개변수를 수정하고 커널 추정 손실의 유도에 따라 구배 역전달 방식으로 를 업데이트합니다.
-
FKP는 랜덤 초기화로 시작하여 커널을 천천히 업데이트하는 대신 학습된 커널 매니폴드를 따라 이동하며 업데이트 중에 신뢰할 수 있는 커널 을 생성합니다.
-
또한 가 다변량 가우스 분포를 따를 때 대부분의 분포 질량은 반지름 의 표면 근처에 있습니다. 여기서 는 의 차원입니다.
-
따라서 저자는 모든 업데이트 후 유클리드 표준 마스크 를 제한함으로써 전체 잠재공간에서의 최적화를 피함으로써, 구면 표면에서의 를 최적화 합니다.
Original Double-DIP
-
DIP는 네트워크 구조가 저수준 이미지 통계를 캡처하는 임의로 초기화된 인코더-디코더 네트워크 G의 형태로 된 이미지 prior입니다.
-
네트워크 파라미터 를 최적화하여 고정 무작위 노이즈 입력 에서 자연스럽게 보이는 영상 를 재구성 합니다.
-
다른 이미지 구성 요소를 모델링하기 위해 DoubleDIP은 이미지 분할과 같은 이미지 분해 작업을 위해 두 개의 DIP를 결합합니다.
-
또한 이 프레임워크는 하나의 DIP를 FCN(Fully-Connected Network)으로 대체하여 이미지 디콘볼루션에서도 활용됩니다.
-
Double-DIP 및 그 변형 모델이 블라인드 SR에 사용되는 경우 다음과 같이 공식화할 수 있습니다.
-
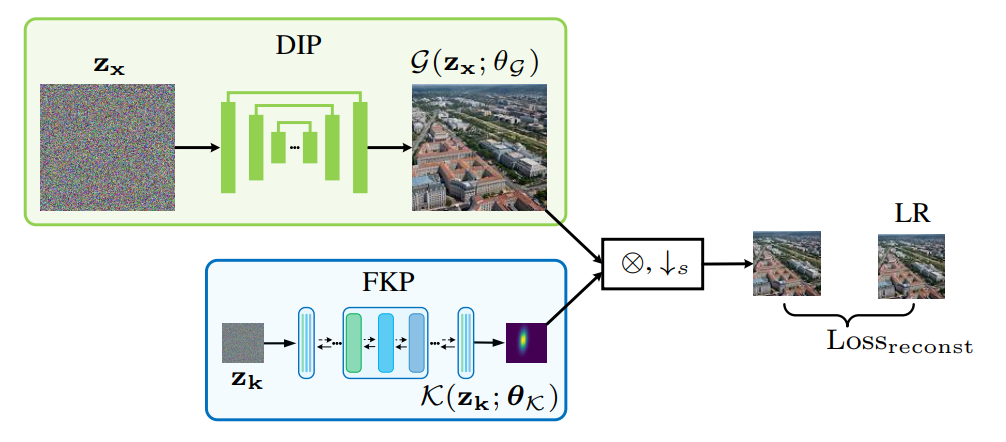
여기서 는 통합 FKP입니다. 그림 3에 해당하는 개략도 그림이 나와 있습니다.
-
DIP-FKP에서는 네트워크 매개변수 가 아닌 커널 잠복 변수 를 최적화합니다. 이는 커널 prior를 모델링한 것과 같습니다.
-
보다 구체적으로, 순전파에서 FKP는 LR 이미지 예측을 얻기 위해서 DIP에 의해 생성된 이미지 를 흐리게 하는 커널 예측 를 생성합니다.
-
결과 LR 예측과 LR 이미지 사이의 평균 제곱 오차(MSE)는 손실함수로 사용됩니다.
-
역전파에서 구배는 손실함수에서 커널예측, 그리고 잠재변수 로 역전파됩니다.
-
FKP를 통해, DIP-FKP는 학습된 커널 매니폴드를 따라 커널 예측을 이동함으로써 네트워크에 커널을 효과적으로 포함시켜 정확하고 안정적인 커널 추정을 가능하게 합니다.
-
따라서 대용량 학습 데이터와 긴 학습 시간 없이 DIP-FKP는 테스트 단계에서 SR이미지와 블러 커널을 동시에 추정할 수 있습니다.
-
주목할 점은 DIP-FKP는 커널을 정확하게 추정 할 수 있지만 자체 학습하므로, SR 영상 재구성에 대한 성능이 제한적입니다.
-
그러한 이유로 저자들은 비시각 모델인 USRNET을 사용하여 커널 추정을 기반으로 최종 SR결과를 생성합니다.
Original KernelGAN
-
단일 이미지에서, 작은 이미지 패치는 서로 다른 척도에 걸쳐 반복되는 경향이 있습니다
-
또한 LR 이미지를 블러 커널로 분해하여 다시 downscale한 LR이미지를 얻을 때 HR과 LR 이미지 사이의 커널이 LR 이미지와 다시 downscale한 LR 이미지 간의 내부 패치 배포 유사성을 최대화하는 것을 확인할 수 있습니다.
-
이러한 관찰에 따르면, KernalGAN은 블러 커널을 추정하기 위해 단일 LR 이미지에 대해 내부 생성 적대 네트워크 (GAN)를 훈련시킵니다.
-
이는 학습 가능한 몇 개의 컨볼루션 레이어를 통해 LR 이미지를 축소하는 딥 linear Generator G와 LR 및 RLR 이미지의 패치 분포를 구분하는 Discriminator D로 구성됩니다.
-
블러 커널은 반복할 때마다 G에서 파생됩니다. 공식적으로 커널GAN은 다음과 같이 최적화되었습니다.
-
여기서 는 LR 이미지에서 임의로 추출된 패치입니다. 즉 와 은 커널 의 추가 정규화를 나타냅니다.
-
보다 구체적으로, 에는 와 바이큐빅 커널 사이의 평균 제곱 오차 뿐만 아니라 커널 픽셀 합계, 경계, 희소성 및 중심성에 대한 기타 정규화 제약 조건이 포함됩니다.
-
그러나 KernalGAN의 성능이 불안정합니다. 또한 여러 정규화 조건으로 인해 하이퍼 파라미터를 선택해야 하는 부담도 있습니다.
-
KernalGAN은 일부 이미지의 취약한 패치 분포로 인해 불안정해질 수 있습ㄴ디ㅏ.
-
즉 여러 커널이 LR이미지와 유사한 패치 배포를 사용해서 RLR 이미지를 생성할 수 있습니다.
-
이 경우 Discriminator는 서로 다른 패치 분포를 구분할 수 없으므로 커널 예측이 잘못됩니다.
-
문제를 완화하기 위해, 우리는 최적화 공간을 제한하기 위해 제안된 FKP를 커널 GAN에 통합할 것을 제안합니다.
-
우리는 이 방법을 다음과 같이 공식화할 수 있는 KernelGAN-FKP라고 부릅니다.
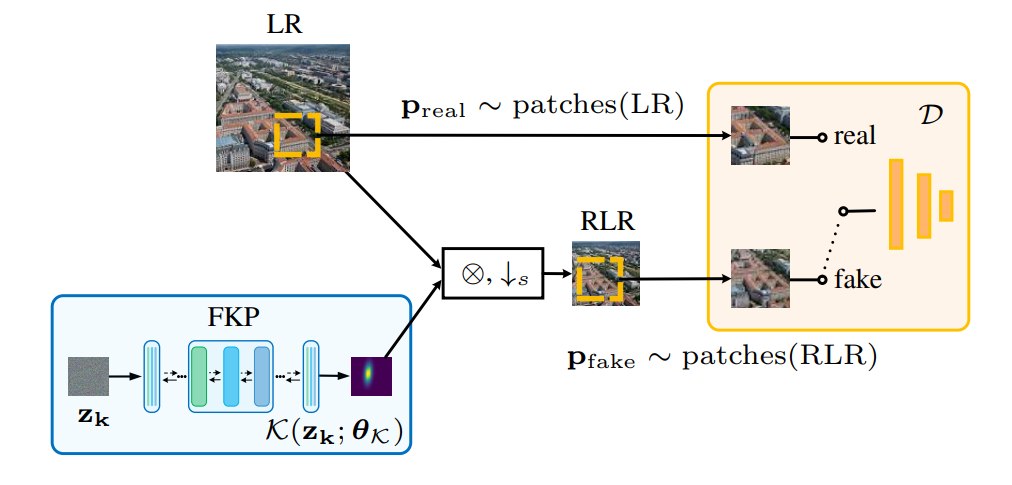
-
그림 4에서 도식적으로 나타낸 바와 같이, 커널GAN-FKP는 잠재 변수 로부터 커널을 직접 생성하여 Deep linear 네트워크를 사용하는 대신 LR 이미지를 저하시키는 데 사용합니다.
-
최적화에서 는 식별자를 속이도록 최적화되었으며, 이는 식별자가 구분할 수 없는 커널을 찾기 위해 커널 공간을 이동하는 것과 같습니다.
-
따라서 Generator의 최적화 공간이 제한되고 커널 생성 품질이 보장되므로 별도의 정규화 조건 없이도 원래 커널 GAN보다 안정적인 융합이 가능합니다.
-
DIP-FKP와 유사하게, 우리는 커널 예측 후 비시각 SR을 위해 USRNet을 채택합니다.
