통계학 기초 02 데이터의 분포
2.1 모집단과 표본
1) 모집단은 전체, 표본은 일부
- 모집단 : 관심의 대상이 되는 전체 집단
- 표본 : 모집단에서 추출한 일부
2) 왜 표본을 사용하는 걸까?
(1) 현실적인 제약
ㄱ. 비용과 시간
- 전체 모집단을 조사하는 것은 비용과 시간이 많이 들기 때문에 대부분의 경우 불가능하거나 비효율적
- 표본 조사는 이러한 자원을 절약하면서 유의미한 결과를 도출할 수 있는 방법
ㄴ. 접근성
- 모든 데이터를 수집하는 것이 물리적으로 불가능한 경우가 많음
ㄷ. 대표성
- 표본의 대표성
- 잘 설계된 표본은 모집단의 특성을 반영, 이를 통해 표본에서 얻은 결과를 모집단 전체에 일반화할 수 있다.
- 무작위로 표본을 추출하면 편향을 최소화하고 모집단의 다양한 특성을 포함 가능
ㄹ. 데이터 관리
- 데이터 처리의 용이성
- 표본 데이터를 사용하는 것은 전체 데이터를 다루는 것보다 데이터 처리와 분석이 훨씬 용이, 큰 데이터셋은 분석에 많은 컴퓨팅 자원이 필요하지만 작은 표본은 부담을 줄여줌
- 데이터 품질 관리
- 작은 표본에서 데이터 품질을 더 쉽게 관리하고 오류나 이상값을 식별하여 수정할 수 있다.
ㅁ. 모델 검증 용이
- 모델 적합도 테스트
- 표본 데이터를 사용하여 통계적 모델을 검증. 모델이 표본 데이터에 잘 맞는다면 모집단에도 잘 맞을 가능성이 높음
ㅂ. 전수조사 : 모집단 전체를 조사하는 방법. 대규모일 경우 비용과 시간이 많이 듦
ㅅ. 표본조사 : 표본만을 조사하는 방법. 비용과 시간이 적게 들지만, 표본이 대표성을 가져야 함
(2) 실제로 어떻게 사용되어 질까?
- 실제로 모든 데이터를 다 수집할 수 없을 때 표본을 사용
- 도시 연구
- 의료 연구
- 시장 조사
- 정치 여론 조사
2.2 표본오차와 신뢰구간
1) 표본오차와 신뢰구간이란?
(1) 표본오차
-
표본에서 계산된 통계량과 모집단의 진짜 값 간의 차이
- 표본 크기가 클수록 표본오차는 작아짐
- 표본이 모집단을 완벽하게 대표하지 못하기 때문에 발생, 표본의 크기와 표본 추출 방법에 따라 달라짐
-
표본의 크기 : 표본의 크기가 클수록 표본오차는 줄어듬
-
표본 추출 방법 : 무작위 추출 방법을 사용
(2) 신뢰구간
-
모집단의 특정 파라미터에 대해 추정된 값이 포함될 것으로 기대되는 범위
-
신뢰구간 계산 방법
- 신뢰구간 = 표본평균 ± z x 표준오차
- 95%의 신뢰수준일 경우, z-값은 1.96
- 일반적으로 95%의 신뢰 수준을 많이 사용
-
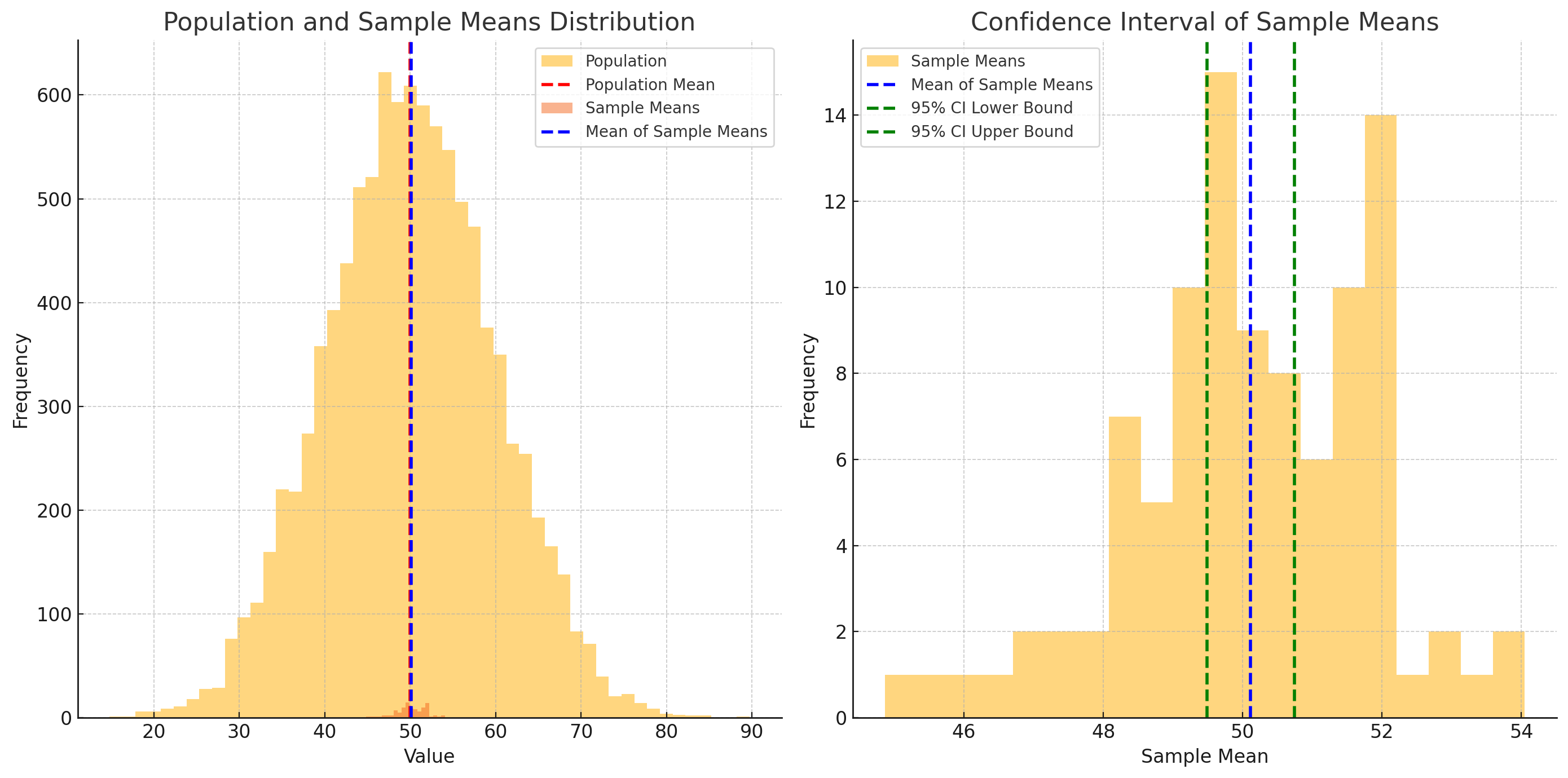
모집단과 표본 분포 (왼쪽 그림)
- 붉은색 점선은 모집단의 평균
- 파란색 점선은 표본의 평균
- 모집단의 분포는 넓고, 표본 평균들의 분포는 좁아집니다.
- 표본 크기가 커질수록 표본 평균이 모집단 평균에 더 가까워지는 경향을 보여줍니다.
-
신뢰구간 시각화 (오른쪽 그림)
- 오른쪽 그림은 표본의 분포와 95% 신뢰구간을 보여줍니다.
- 파란색 점선은 표본의 평균을 나타내고, 녹색 점선은 95% 신뢰구간의 상한과 하한을 나타냅니다.
- 이 신뢰구간은 모집단의 평균을 포함할 것으로 예상되는 범위입니다.
2) 실제로 어떻게 사용될까?
- 수학점수 표본으로부터 모집단의 평균 범위를 계산
- scipy.stats.t.interval(alpha, df, loc=0, scale=1)
- alpha
- 신뢰 수준(confidence level)을 의미합니다. 예를 들어, 95% 신뢰 구간을 원하면
alpha를 0.95로 설정합니다.
- 신뢰 수준(confidence level)을 의미합니다. 예를 들어, 95% 신뢰 구간을 원하면
- df
- 자유도(degrees of freedom)를 나타냅니다. 일반적으로 표본 크기에서 1을 뺀 값으로 설정합니다 (
df = n - 1).
- 자유도(degrees of freedom)를 나타냅니다. 일반적으로 표본 크기에서 1을 뺀 값으로 설정합니다 (
- loc
- 위치(parameter of location)로, 일반적으로 표본 평균을 설정합니다.
- scale
- 스케일(parameter of scale)로, 일반적으로 표본 표준 오차(standard error)를 설정합니다. 표본 표준 오차는 표본 표준편차를 표본 크기의 제곱근으로 나눈 값입니다 (
scale = sample_std / sqrt(n)).
- 스케일(parameter of scale)로, 일반적으로 표본 표준 오차(standard error)를 설정합니다. 표본 표준 오차는 표본 표준편차를 표본 크기의 제곱근으로 나눈 값입니다 (
2.3 정규분포
1) 정규분포
- 종 모양의 대칭 분포로 평균 주위에 몰려 있는 분포
- 평균을 중심으로 좌우 대칭, 평균에서 멀어질수록 데이터의 빈도가 감소
- 표준편차는 분포의 퍼짐정도
- 특징 : 대부분의 데이터가 평균 주변에 몰려 있으며, 평균에서 멀어질수록 빈도가 줄어듦.
2) 실제로 어떻게 사용될까?
- 데이터 수가 많을 경우 대부분의 경우 사용 가능
- 중심극한정리
2.4 긴 꼬리 분포 ( Long Tail )
- 대부분의 데이터가 분포의 한쪽 끝에 몰려있고, 반대쪽에 긴 꼬리가 이어지는 형태의 분포
- 정규분포와 달리 대칭적이지 않고 비대칭적
- 소수가 큰 영향을 미칠 때 활용 (20 : 80)
- 특정한 하나의 분포를 의미하지 않으며 여러 분포의 분포(예: 파레토 분포, 지프의 법칙, 멱함수)를 포함
- 특징 : 소득 분포, 웹사이트 방문자 수 등에서 관찰
2.5 스튜던트 t 분포
- 표본이 적을 때 정규분포 대신에 사용하는 분포
- 자유도가 커질수록 정규분포에 가까워짐
- 자유도 : 변수들이 얼마나 제한없이 자유롭냐?를 확인하기 위한 것
- 모집단의 표준편차를 알 수 없고, 표본의 크기가 작은 경우(일반적으로 30 미만)
2.6 카이제곱분포
- 독립성 검정, 적합성 검정에서 사용(유사도 검정에서 사용)
- 범주형 데이터의 독립성 검정이나 적합도 검정에서 사용되는 분포
- 특징
- 자유도에 따라 모양이 달라짐
- 상관관계나 인과관계를 판별하고자 하는 원인의 독립변수가 '완벽하게 서로 다른 질적 자료'일 때 활용
예) 성별이나 나이에 따른 선거 후보 지지율 - 범주형 데이터 분석에 사용
- 독립성 검정이나 적합도 검정이 필요할 때
- 독립성 검정 : 두 범주형 변수 간의 관계가 있는지 확인할 때 사용
- 적합도 검정 : 관측한 값들이 특정 분포에 해당하는지 검정할 때 사용
2.7 이항분포
-
결과가 2개가 나오는 상황일 때 사용하는 분포
- 연속된 값을 가지지 않고, 특정한 정수 값만을 가질 수 있기 때문
- 이산형 분포라고도 지칭
- 성공/실패와 같은 두 가지 결과를 가지는 실험을 여러 번 반복했을 때 성공 횟수의 분포
- 독립적인 시행이 n번 반복되고, 각 시행에서 성공과 실패 중 하나의 결과만 가능한 경우를 모델링하는 분포
- 성공 확률을 p라 할 때, 성공의 횟수를 확률적으로 표현
-
특징 : 실험 횟수 (n)와 성공 확률(p)로 정의
2.8 푸아송 분포
-
희귀한 사건이 발생할 때 사용하는 분포
- 이항 분포처럼 연속된 값을 가지지 않기 때문에 이 분포도 역시 이산형 분포에 해당
- 평균 발생률 (람다)가 충분히 크다면 정규분포에 근사
- 평균 발생률이란 주어진 시간이나 공간에서 사건이 몇번 발생했는지
-
포아송 분포
- 단위 시간 또는 단위 면적 당 발생하는 사건의 수를 모델링할 때 사용하는 분포
- 단위 시간 또는 단위 면적당 희귀하게 발생하는 사건의 수를 모델링하는데 적합
-
특정 공간이나 특정 시간에 사건이 발생하는 경우
- 콜센터
- 교통사고
- 문자 메시지
- 웹사이트 트래픽
2.9 분포 정리하기
- 데이터 수가 많아지면 정규분포에 수렴(중심극한정리)
- 데이터 수가 많으면 정규분포
데이터 수가 충분하다 - 정규분포
데이터 수가 작다 - 스튜던트 t 분포
일부 데이터가 전체적으로 큰 영향을 미친다 - 긴꼬리 분포
범주형 데이터의 독립성 검정이나 적합도 검정 - 카이제곱 분포
결과가 두개만 나오는 상황 - 이항 분포
특정 시간, 공간에서 발생하는 사건 - 푸아송 분포