기저법

기저법(Offset-Binary)과 실수형 지수 표현의 비밀

<자바의 정석 3판 77pg>

 실수형 간의 형변환에서 작은 타입(float)에서 큰 타입(double)으로 변환시 지수(E)는 float의 기저인 127을 뺀 후 double의 기저인 1023을 더해 반환하고, 가수(M)는 float의 가수 23자리를 채우고 남은 자리를 0으로 채운다. 지수의 변화보다는 가수의 변화를 눈여겨보자.

여기서의 기저는 무슨 말일까?

1. 정수 표현 방식 간단 정리

2진수에서 부호 있는 정수를 표현하는 방법은 여러 가지가 있습니다. 대표적으로 아래 방식들이 존재하며, 이 중 가장 널리 쓰이는 것이 바로 2의 보수법과 기저법(Offset-binary) 입니다.

• 부호화 절대값
• 1의 보수법
• 2의 보수법
• 기저법(Offset-binary)

2. 부호화 절대값 표현

MSB(Most Significant Bit)를 부호비트로 사용하는 방식

MSB값	의미
0	양수
1	음수

문제점: +0과 -0 두 개의 0이 존재함
덧셈 연산 비효율 → 보수 표현 방식 등장

3. 보수 표현법

보수란?
어떤 수에 더하면 밑수가 되는 수.
예: 10진수에서 2의 10의 보수는 8 (2 + 8 = 10)

• 1의 보수 → 각 비트를 반전
• 2의 보수 → 1의 보수 + 1

ex) 음수 2의 보수 구하기 (예: -5)
  1. 절대값 5 → 이진수: 0101
  2. 1의 보수: 1010
  3. 2의 보수: 1010 + 1 → 1011

절대값	2진수	1의보수	2의보수
5	0101	1010	1011

4. 기저법(Offset-Binary)이란?

기저법은 음수를 양수처럼 저장하기 위한 방식입니다.
부동소수점에서 지수부는 양/음수 모두 표현해야 하기 때문에 기저를 사용해 부호 없는 값으로 변환합니다.

• 기저(Bias): 양/음 지수를 양수로만 저장하기 위한 보정값

  ex) float → bias 127, double → bias 1023

기저법 동작 원리
float 지수 범위: -127 ~ 128 → bias 값: 127

ex) 지수 값이 5일 때
저장 값 = 실제 지수 + bias = 5 + 127 = 132
읽을 때는?
실제 지수 = 저장된 값 - bias = 132 - 127 = 5

5. float → double 형변환 시 지수 변환

1. float에 저장된 지수: 132
2. float bias: 127
3. 실제 지수: 132 - 127 = 5
4. double bias: 1023
5. double에 저장할 지수: 5 + 1023 = 1028

이렇게 지수 보정을 해줘야 실제 값이 유지됩니다.

6. 부동소수점 구조

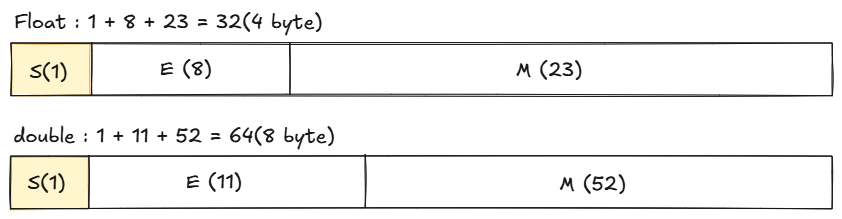
구분	기호	설명
부호 비트	S	0: 양수, 1: 음수
지수부	E	bias가 적용된 지수값 (float: bias 127, double: bias 1023)
가수부	M	실수값의 유효숫자. (float 23비트, double 52비트)

7. 왜 기저법을 쓸까?

1) 정렬 및 비교 최적화
→ 부호 고려 없이 정수처럼 비교 가능
2) 덧셈/뺄셈 단순화
→ 지수 정렬이 쉬워짐
3) 하드웨어 연산 최적화
→ 부호 처리 없이도 연산 수행 가능

8. 한줄 요약!

• 기저법은 부호 있는 지수값을 양수로 저장하기 위한 방법
• float, double은 기저값이 다르므로 형변환 시 지수 보정이 필수
• 가수(M) 는 자리수를 늘리고 남은 자리를 0으로 채움
• 기저법을 통해 빠르고 정확한 부동소수점 연산이 가능해짐

참고
• 《자바의 정석 3판》 77페이지
• IEEE 754 부동소수점 표준
https://hunbae.tistory.com/12?category=1197695